竹材介电性质研究

徐世克，汤 颖，章卫钢，俞旭锋，潘恩琴，李延军

（浙江农林大学工程学院，浙江 临安 311300）

竹材介电系数和介质损耗角是竹材介电性质的重要组成因子，是表明竹材在交变电场下介质极化和储存电能能力的一个量，不仅对竹材高频、微波加热和竹材含水率的测量具有重要意义，而且能加快高频微波加热、软化在竹材加工中的应用，同时为竹材密度检测提供依据。高频和微波加热技术主要利用木竹材介电性质来进行木竹材的干燥、胶合、软化、含水率测定等[1]。目前，国内学者对射频下和微波频率下等不同频率段的常见树种进行了介电性能的研究[2～5]。而国外学者对木材介电性质在较广泛的范围内作了研究[6～12]。但是国内外对竹材的介电性质研究较少，本文拟通过对竹材含水率、纹理、频率等因素对竹材介电性质的影响进行系统研究，借鉴木材干燥时高频常用频率为7 ～ 13.6 MHz，在酚醛和脲醛胶胶合时频率为13.5 MHz，主要针对竹材在高频频率范围内的介电性能进行研究。

1 材料与方法

1.1 试验材料

试验材料毛竹取自浙江省临安市，选取不同竹龄的毛竹，将其剖分后制备成相同长度的竹片，将竹片按毛竹同一部位不同的纹理方向胶合成100 mm×40 mm×20 mm（长×宽×厚）的小竹方，再锯制成直径30 ～ 40 mm，厚度2.0 ± 0.5 mm的圆形薄竹片，用砂纸打磨光滑，使其厚薄均匀。实验干燥后，放入干燥器内，按照实验要求，利用调温调湿箱调节含水率。

1.2 试验方法

研究竹材纹理方向（横向、径向、弦向）、含水率（0% ～ 50%）、频率（主要选取高频射频频率段附近60 kHz ～ 13 MHz）、不同部位（节子、节间）、竹龄（1、2、4、6 a）等因素对毛竹介电常数和介质损耗角的影响及其相互之间的关系。

采用介电常数测试仪（STD-A），在恒定温度20℃环境中进行测试，根据试验需要选取电感，调整测试仪器频率，一般为和电感相匹配的频率。电感值为0.1 μH ～ 250 mH共7档，可调频率范围为：100 kHz ～ 50MHz。介电常数计算方法：

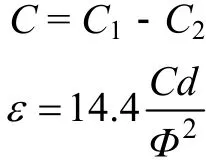
式中：C为试样的电容量（PF），C1为未放试样测量电容，C2为放入试样测量电容，ε为介电常数，d为试样厚度（m），Ф为试样直径（m）。

介质损耗正切角tanδ计算方法：

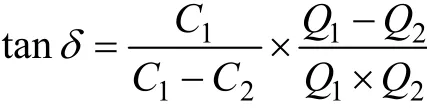
式中，Q1为未放试样测量电感；Q2为放入试样测量电感。

2 结果与分析

2.1 纹理方向对竹材介电常数的影响

从图1可以看出，在同含水率、温度、频率下测得不同纹理方向毛竹的介电常数，竹材横向介电常数明显大于弦向和径向的介电常数，弦向介电常数和径向介电常数相差不大。这主要与竹材的各向异性有关，竹材以纵向纹理为主，纤维长宽比比较大[13]，这就有利于各种物质和能量在纵向的传导；微观结构上，竹材的的组织大部分也是纵向的，因而竹材分子在纵向具有更大的活化能。在电场条件下，竹材在纵向的电流传导远远大于径向和弦向，弦向和径向的传导受到纵向组织的阻碍，竹材横向分子官能团具有更大的自由度，能产生较大的活化能，因而介电常数相对于其他两个方向要大些。

2.2 含水率对竹材介电常数的影响

从图1可知，竹材介电常数随着含水率的增加有显著增加趋势，介质损耗角正切值tanδ也随含水率升高而明显增大。在低于纤维饱和点时，随含水率的增加，介电常数增加比较缓慢；在纤维饱和点附近时，竹材介电常数随着含水率的增加而急剧增大；在含水率高于纤维饱和点时，含水率和介电常数近似成线性关系。

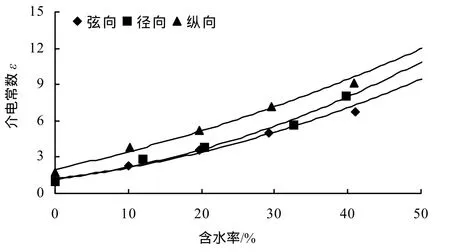
图1 不同纹理方向竹材介电常数随含水率的变化Figure 1 Effect of bamboo texture on dielectric constant

竹材从绝干开始随着含水率的增加，竹材中结合水的含量逐步提高，水的介电常数比较高（81）[13]，因此竹材介电常数会随着竹材中水分的增加而提高。在纤维饱和点以下时，竹材细胞的结合水还未处于饱和状态，竹材分子的官能团自由度比较小，分子运动能量小，影响了电流的传导，介电常数增加就比较缓慢。当竹材含水率继续增加，随着竹材中结合水含量增加，在电场作用下竹材内部的分子运动急剧增加，活化能提高，在竹材纤维饱和点附近竹材分子运动剧烈，运动加速，电流传导随之加大，介电常数明显提高；当含水率高于纤维饱和点时，结合水不再增加，竹材中的自由水不断增加，此时竹材结合水对介电常数的影响不再起主导作用，自由水开始发挥主导作用，随着自由水含量的增加，竹材分子运动速度减慢，竹材介电常数和含水率成线性相关关系。

2.3 频率对竹材介电性能的影响

图2、图3为不同纹理方向的气干毛竹材在不同的频率下测量的介电常数和介质损耗角正切值。

由图2、图3可知，3个纹理方向竹材介电常数均随着测量频率的增大而减小；介质损耗角正切值也随着频率增大逐渐减小。从60 kHz到600 kHz介电常数随着频率的增加，降低明显；从600 kHz到6 MHz，介电常数随着频率的增加变化不显著；频率大于6 MHz后，介电常数随着频率的增加而明显增加。

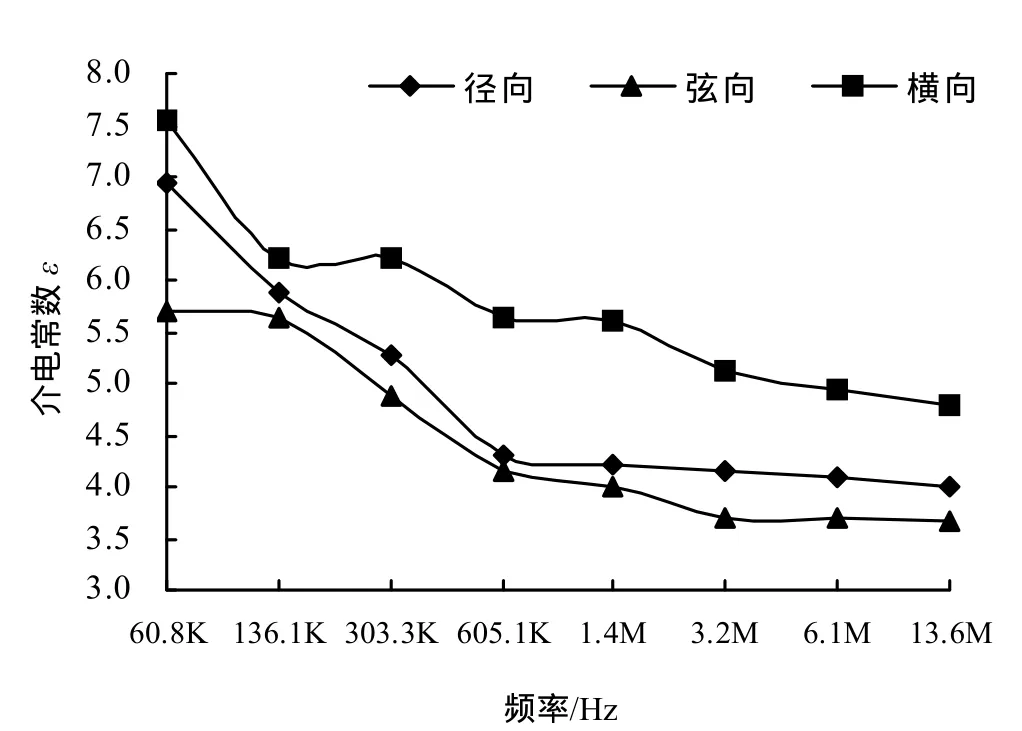
图2 介电常数随频率变化Figure 2 The dielectric constant and frequency

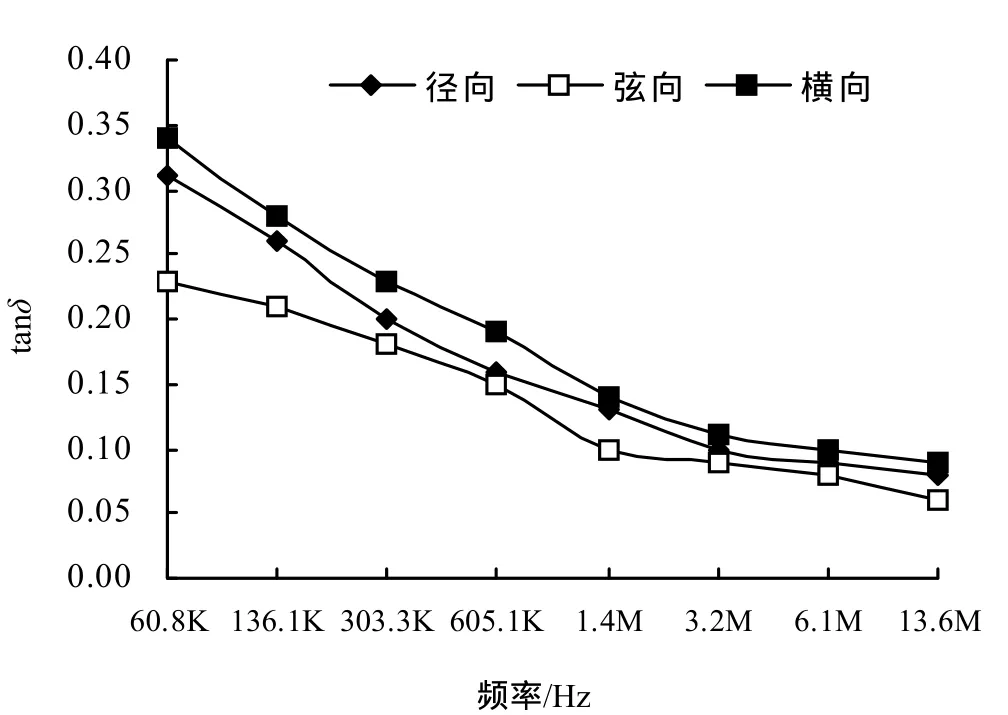
图3 介质损耗角正切值随频率变化Figure 3 The tanδ of dielectric loss and the frequency

在低频率下，竹材中一部分水分子和组织分子中的自由基随着电流的变化而运动被激活，随着频率的不断升高，竹材内部一部分水分子和组织分子自由基运动变化速度来不及跟上频率的变化，被激活的自由基数目减少，电流在竹材内部的传导减少，介电常数逐渐减小。当频率大于600KHz后，竹材内部一部分分子运动来不及随着频率的变化速度，介电常数减少缓慢。

2.4 不同竹龄和部位毛竹介电性能的变化

由表1可知，相同频率（13.6 MHz）和相同含水率（12%）条件下测试不同竹龄竹材的介电系数ε和损耗角正切tangδ时，介电常数ε先随着竹龄增长而变大，4年左右最大，后又减小。介电常数随着竹龄的变化规律与毛竹的生长特性有关，竹材密度随着竹龄的增加逐渐增大，4年左右毛竹密度最大，介电常数也最大，之后随着竹龄的增加，竹材逐渐到了老化年龄，密度逐渐减小，介电常数随之减小。

相同含水率（12%）、温度（20℃）、频率（13.6MHz）条件下测试竹节部与竹间部位的介电常数。介电常数：节子 ＞ 节间。介质损耗角正切值：节间 ＞ 节子。节间部位介电常数比节子部位大，但是差别不显著。

对于竹材，一方面节子部位的木质化现象比较严重，纤维素含量高，节子密度大于节间密度[13]，细胞壁物质含量大。另一方面节子部位分子官能团自由基数目比节间部分多，在电场中被激活的自由基数目增加，电流传导加速，介电常数随之增大。

表1 毛竹介电常数和介质损耗正切角Table 1 The dielectric constant and dielectric loss of bamboo culm

3 结论

（1）毛竹材横向介电常数大于径向、弦向介电常数，径向弦向介电常数差别不明显。

（2）介电常数随着竹材含水率不同变化显著，在纤维饱和点附近，竹材介电常数随着竹材含水率不同变化显著，高于纤维饱和点时，介电常数和竹材含水率近似成线性关系；

（3）竹材介电常数随着电场频率的增加而减小，变化显著，当电场频率高于600 kHz后，介电常数随着电场频率的增大变化缓慢。

（4）竹材年龄和竹节对竹材介电性能的影响，主要是因为竹材密度和竹材材质的不同，规律相对简单，具体规律不显著。

[1]尹思慈. 木材学[M]. 北京：中国林业出版社，1996.

[2]陈爱平，李伟，吴晓波，等. 竹材内耗和介电的研究[J]. 南京大学学报（自然科学版），2005，41（4）：364－369.

[3]李先泽. 射频下木材的介电性质[J]. 林业科学，1964，9（3）：232－244.

[4]周曼. 关于木材介电性质的研究[J]. 江苏林业科技，1996，23（3）：62－64.

[5]季亚春，季亚坤. 木材介电常数的测量[J]. 黑龙江电子技术，1997（5）：24－27.

[6]Ramasamy S, Moghtaderi B. Microwave characterization of typical Australian wood-based biomass materials[J]. AIP Conf Proc, 2009（1096）：1558－1565.

[7]Ay N, Sahin H. Dielectric constant of Turkish timbers in the longitudinal direction at a 9.8-GHz frequency[J]. For Prod J, 2004, 54（10）：65－68.

[8]Schinker M G, Hansen N, Spiecker H. High-frequency densitometry-a new method for the rapic evaluation of-wood density variations[J]. Iawa J, 2003, 24（3）：231－239.

[9]Suzuki Y, Kuroda N. Dielectric properties of wood with high moisture content[J]. Mokuzai Gakkaishi, 2003, 49（3）：161－170.

[10]Yokoyama M, Ohmae K, Kanayama K. Mechanical and dielectric relaxations of wood in a low temperature range[J]. Mokuzai Gakkaishi, 2000,46（6）：523－530.

[11]Kabir M F, Daud W M，Khalid K B,et al. Equivalent circuit modeling of the dielectric properties of rubber wood at low frequency[J]. Wood Fib Sci, 2000, 32（4）：450－457.

[12]Khalid K B, Kabir M F, Daud W M,et al. Multi-component mixture modeling for the dielectric properties of rubber wood at microwave frequencies[J]. HolzForschung, 1999, 53（6）：662－668.

[13]刘一星，赵广杰. 木质资源材料学[M]. 北京：中国林业出版社，2004.