PCB内层芯板补偿系数预估：实验和统计学方法

邓 丹 张岩生 刘 东 宋建远

深圳崇达多层线路板有限公司

王立全 吴丰顺

华中科技大学

1 引言

随着电子产品的高密度、多功能、小型化发展，尤其是HDI基板产品的不断增多，使得PCB制造厂商需要不断的提高工艺技术以使其不被激烈的市场竞争所淘汰。而困扰着我们的一个重要问题是如何在PCB产品生产之前预估其最终的变形量（如图1所示），从而准确的给出图形补偿系数。

图1 PCB产品的变形量

此前已经有学者和工程师在这方面做了许多研究，通过应力变形计算或者有限元模拟的方法分析多层板层压过程，建立了内应力完全释放与不释放两种数学模型，模拟了压合变形的整个过程，介绍了利用线性和非线性方法进行补偿系数分析校准的过程和讨论，总结出内层收缩的两大主要影响因素为残留内应力和热涨系数不匹配。本研究的目的是找到一种简单且准确的方法来预测工程上所需的图形补偿系数，从而给补偿系数工程师提供可靠的辅助工具。

2 实验方法

从影响涨缩的鱼骨图（如图2）图形中可以看到PCB图形的涨缩受到诸多因素的影响，包括板料厂商、芯板厚度、铜厚、残铜率、压合结构、季节变化等等。但在材料一定的情况下，影响芯板补偿系数的主要为芯板板厚、铜厚和残铜率三因素。

图2 影响涨缩的因素分析

正交实验方法被应用到本实验中以研究上述三因素对涨缩系数的影响。实验参数明细如表1所示。实验流程如图3所示。菲林图形涨缩PAD采用二次元进行测量，测量精度为0.1μm。压合后涨缩PAD测量采用X-Ray打靶机进行测量，测量精度为1μm，因此所有测量数据精确到1μm 。

此实验为三因素三水平实验，所以采用L9(34)正交表进行优化。实验的指标为芯板经纬向涨缩系数。

表1 实验参数明细

图3 实验流程

3 实验结果与讨论

3.1 单因素分析

表2显示不同参数组合下芯板经纬向涨缩系数值，图4和图5为各因素主效应图。图形显示，残铜率对纬向补偿系数的影响主要表现在残铜率为50%以下时，随残铜率降低补偿系数线性变大，当残铜率大于50%时此因素对芯板涨缩系数影响不显著；芯板铜厚对纬向补偿系数的影响表现为随铜厚增加，补偿系数近似线性增长且影响显著；芯板（不含铜）厚度对纬向补偿系数的影响纬向上表现为0.13 mm（不含铜）厚度的芯板涨缩系数较0.075 mm和0.2 mm（不含铜）厚度的芯板低2×10-4。经向方向，残铜率和芯板铜厚对补偿系数的影响接近线性，且随残铜率降低，补偿系数线性变大；随芯板铜厚增加，补偿系数线性变大。

3.2 交互作用分析

表2 各组参数所得补偿系数

图4 纬向补偿系数主效应图

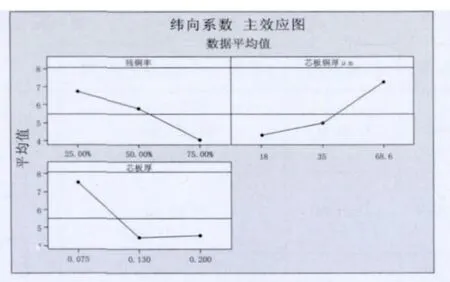
经向补偿系数主效应图

图6和图7显示了纬向和经向方向所研究的三因素两两之间的交互作用。对于纬向系数，残铜率与其他两因素的交互作用主要表现在残铜率为75%时出现的变化规律异常，表现为残铜率为75%的芯板补偿系数随其他两因素变化小于0.5/万，芯板铜厚与芯板厚直接无明显交互。经向上，残铜率与其他两因素的交互作用主要表现在残铜率为50%时出现变化规律异常，表现为芯板补偿系数在残铜率为50%时，与铜厚为2OZ和芯板（不含铜）厚度为0.075mm交互作用下出现系数变大，芯板铜厚与芯板厚的交互作用表现为铜厚1OZ和板厚0.13mm时补偿系数变大。

3.3 . 回归假设及验证

图6 纬向补偿系数交互作用图

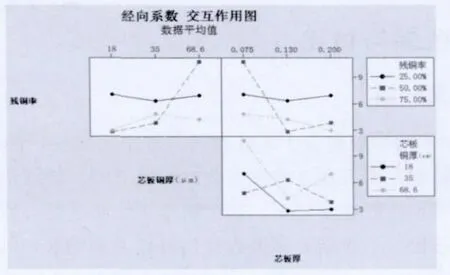
图7 经向补偿系数交互作用图

从主效应图中可以看出残铜率和芯板铜厚对补偿系数的影响为近似线性，而芯板厚度对补偿系数的影响近似二次曲线。表3为纬向方向上四种回归模型的回归结果以及对比。对比表3中的四个公式的回归结果，不难发现，模型2的方程总体P值最小，且小于0.05表明方程总体结果显著。对其中的五个系数的P值进行分析显示，常量、残铜率、芯板铜厚所对应的P值均小于0.05属于显著水平，但芯板厚和板厚平方的系数P值大于0.05属于不显著水平。综合方程总P值，模型2回归模型虽然在单因素描述上存在一定误差，但总体结果能够较为准确的预测纬向涨缩系数。

表4为经向方向上四种回归模型的回归结果以及对比。对比表4中的四个公式的回归结果，模型4的六个系数的P值均小于0.05，其中常量、残铜率、芯板铜厚所对应的P值均小于0.01属于非常显著水平，芯板厚、板厚平方和芯板铜厚×板厚的系数P值小于0.05属于显著水平。回归模型4的整体P值小于0.01表明回归结果非常显著，因此公式模型能够很好的对经向系数进行预测。

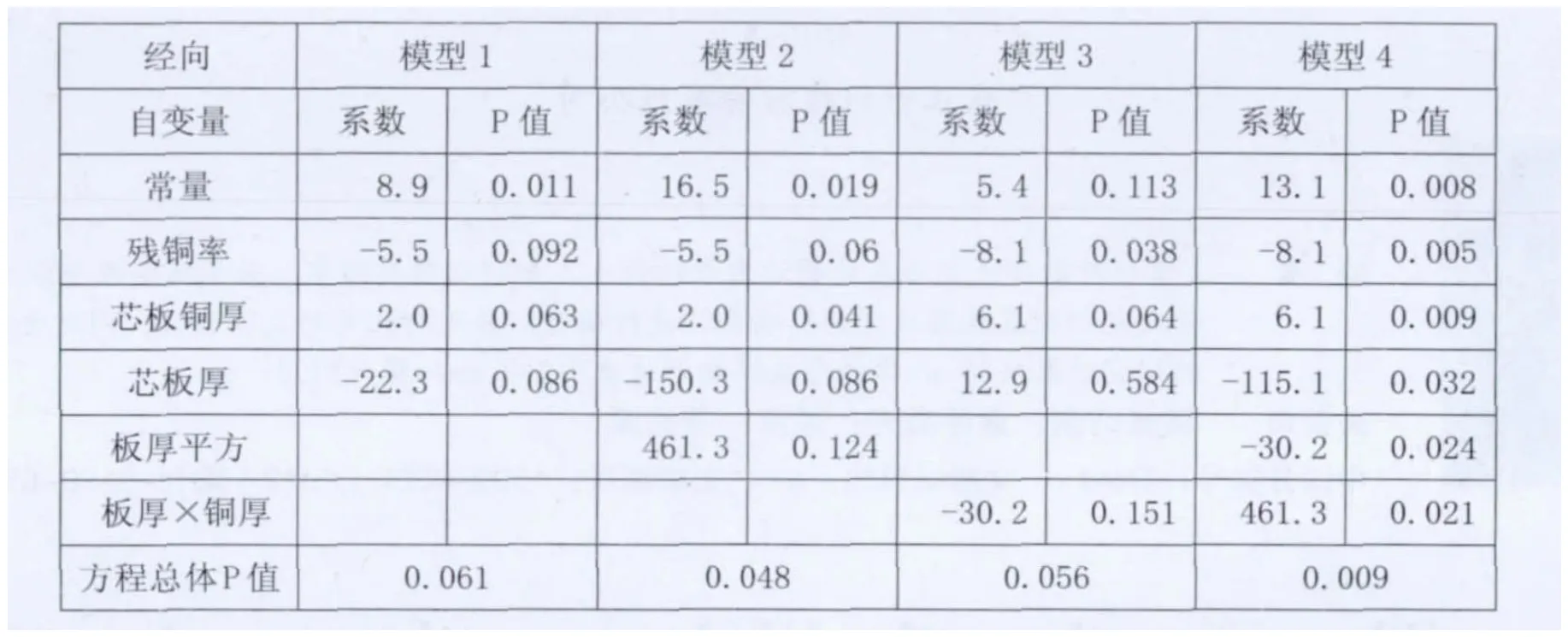
表4 经向回归结果比较

4 总结

在现有生产条件下，我们对某种常用板料进行了补偿系数研究，试验的主要结果概括如下：

（1）残铜率芯板补偿系数的影响接近线性，且残铜率小于50%时补偿系数随残铜率变小变化较大；

（2）芯板铜厚对补偿系数的影响未线性，补偿系数随铜厚增加而近线性变大；

（3）芯板厚度对补偿系数的影响较为复杂，可近似用二次型进行描述；

（4）经向方向，芯板厚度和芯板铜厚存在明显交互作用，将其引入经向回归模型中对模型精度有较大改善。

此实验结论可以为以后建立完整的补偿系数预测机制打下基础，以使其能够尽快的应用到实际生产中的补偿系数预测。

[1]孔令文. 多层板内层收缩的测量与分析[J]. 印制电路信息, 2002

[2]邓丹, 吴丰顺等. 多层板层压过程中的尺寸收缩分析[J]. 印制电路信息, 2010(Z1).

[3]邓丹, 许鹏等. 多层板层压过程中的尺寸收缩分析(二)[J]. 印制电路信息, 2011(S1).

[4]Peng XU， Dan Deng， et al. Deformation Analysis of Multilayer Board in the Lamination Process[D]. 2010 International Conference on Electronic Packaging Technology & High Density Packaging (ICEPT-HDP).

[5]Andrew Kelly. Using both linear and non-linear dimensional analysis, correction and prediction to improve PCB yields[J]. Circuit World, Vol. 33 Iss: 4.

[6]何为. 实验优化设计方法及数据分析[M]. 化学工业出版社, 2012.