双边剪剪刃运动轨迹研究

王喜春

我国在近年相继自行设计并建造了多套中厚板热轧生产线，其中的双边剪被用于同时剪切钢板宽度方向的两个边部，保证钢板宽度尺寸及边部质量。

为消化吸收国外先进技术，进一步提升双边剪设计的理论水平，本文通过离散做图法及数学公式法两种方式，深入研究双边剪的运动轨迹。

1 离散法研究：在剪刃上取点

根据设备结构，建立双边剪的机构原理图（见图1）。以上剪刃圆弧中点为原点，建立相对坐标系X′FY′。以下剪刃中心为原点建立绝对坐标系XOY。以曲柄与X轴夹角α和β为变量分度，在360°范围内每5°为一个相位位置。α、β角以相同的转速转动，以α角旋转360°为一个工作周期。

由机构图可见，上剪刃以R为半径的圆弧上的各点在相对坐标系X′FY′中的相对坐标是固定不变的。坐标系X′FY′在绝对坐标系XOY中做平动和转动，平动时F点的纵坐标Fy发生变化，同时相对坐标系X′FY′绕F点转动，即上剪刃直边与下剪刃的夹角发生变化。

图1 双边剪机构图

在已知设备各结构参数的条件下，可通过三维制图，然后设定α与β角的不同相位，测量不同转角条件下的Fy和γ值。作者使用Inventor三维软件完成实体造型，并对我公司生产的4300 mm双边剪和3500 mm双边剪进行研究，由于每隔5°取值太多，本文只列出其中一些特定角度。两台双边剪除几个重要参数外，其他结构参数均相同（见表 1）。

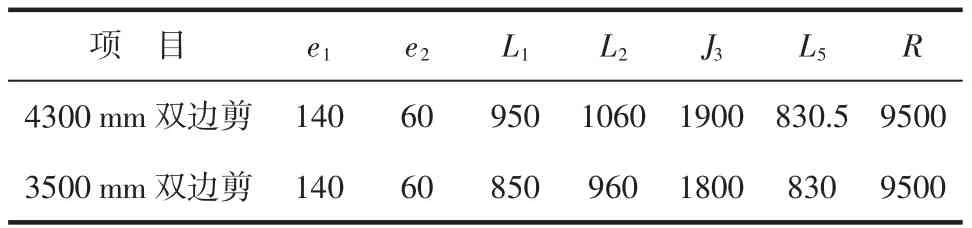
表1 双边剪设备结构参数

在上部圆弧剪刃上取点（见表2），设定各点的相对坐标X′，其相对坐标Y′则由下式确定：

表2 双边剪上剪刃取点

设定α角的三个不同相位，分别是上剪刃左端点最低位置、中间点最低位置、右端有效点最低位置，并测得给定转角条件下的Fy和γ值（见表3）。

表2中的上剪刃各点在相对坐标系X′FY′中的相对坐标通过坐标变换可以转换成绝对坐标系XOY中的绝对坐标，公式如下：

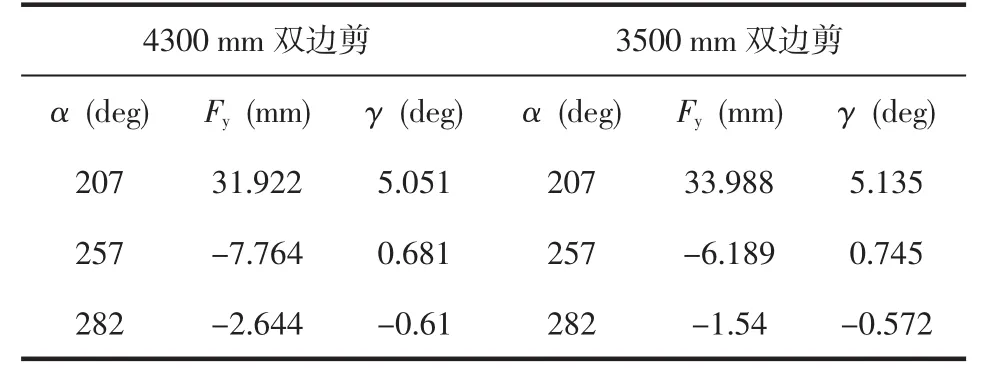
表3 双边剪特定相位角条件下的Fy和γ

4300 mm双边剪与3500 mm双边剪转换后的绝对坐标可以分别计算得到，在三个给定角度下可以描出上剪刃的运动轨迹（见图2、图3）。

可以看出，在剪切过程中上剪刃从左端滚切到右端，最右端点在50 mm以上，则钢板最厚可以允许剪切到50 mm，纵坐标为0的X轴相当于下剪刃，4300 mm双边剪上下剪刃重合点位置在14点附近，3500 mm双边剪在13点附近；由此可得出，4300 mm双边剪上下剪刃重合段长度为1196 mm，3500 mm双边剪为1104 mm，由于双边剪剪切厚度为5～50 mm，且要求剪切送进步长在钢板厚度小于40 mm条件下为1300 mm，可知两种双边剪在剪切薄钢板时无法满足。

因此需进一步研究改变连杆长度或曲轴偏心、下剪刃相对位置等参数对上剪刃运动轨迹的影响，但如果采用上述作图法，则需要做出大量不同参数下的三维图以获取大量测量点进行比较，工作量非常大，而且不能作到取连续点。

而如能推导出剪刃轨迹以上述参数为变量的方程，则工作量可大大减少。

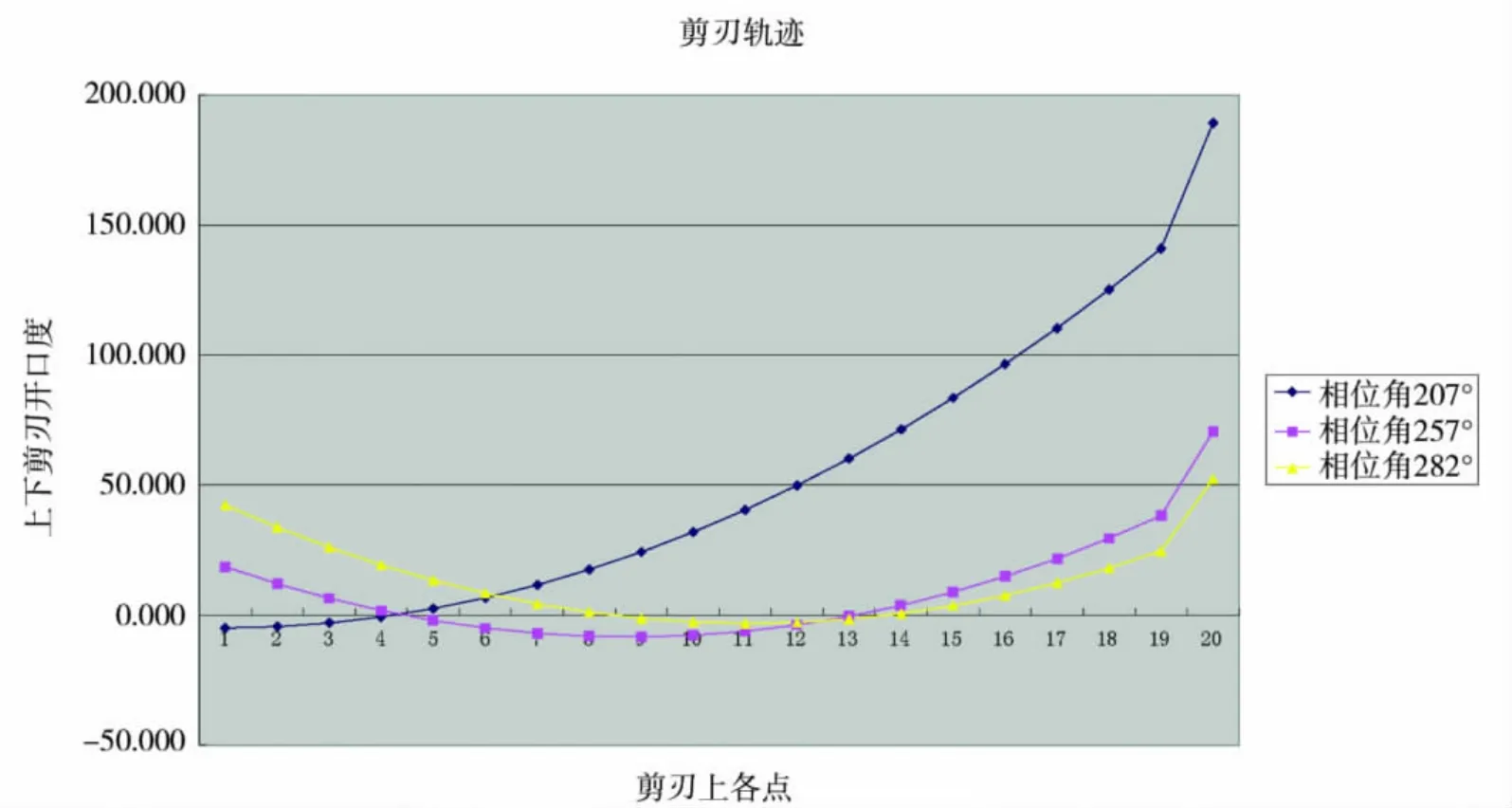
图2 4300 mm双边剪上剪刃轨迹

图3 3500 mm双边剪上剪刃轨迹

2 数值法研究：推导通用方程

双边剪机构在绝对坐标系XOY中各点坐标如下：

入口固定铰点M(J2，J3)；出口固定铰点N(J2-J1，J3)；入口曲柄连杆铰点A(Mx+e1cosα，My+e1sinα)；出口曲柄连杆铰点 C(Nx+e2cosβ，Ny+e2sinβ)；出口连杆与上剪刃座铰点D(Dx，Dy)；上剪刃中点到铰点DB连线的垂足点E(Ex，Ey)；入口曲柄连杆铰点B(Bx，By)；上剪刃中点F(0，Fy)。

按坐标与距离关系式得出如下方程：

以上 8 个方程中，只有 Bx、By、Dx、Ex、Ey、γ共8个未知数，可以求出Fx和γ。

用迭代法推导出关系式方程

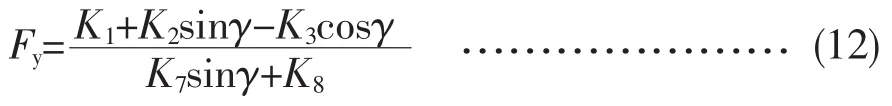
设sinγ=x，则可最终导出式 (35)高次方程。

以下为方程的中间变量：

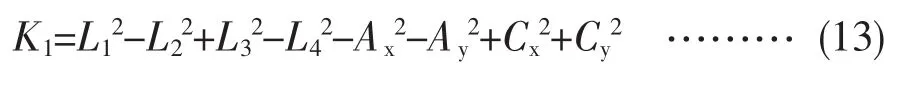
而最终方程的系数

则最终高次方程

由切线法或弦位法可求得x5值，从而得出

另外，由式（12）可求得Fy。

求得Fy及γ后，由相对坐标系X′FY′与绝对坐标系的关系，通过坐标变换，即可计算出剪刃上任意一点的绝对坐标值。

3 数据分析

为了验证数学公式的准确性，将相同参数下作图法与数值法结果进行对比（见表4）。

可见绝对偏差值非常小，如果取相对偏差最大值为万分之三，则在工程计算中可以认为非常准确。

从以上对比数据可看出，如果想增加双边剪上下剪刃重合段的长度，在α为282°时增加入口连杆长度L1或入口偏心轴偏心距e1效果最直接，但为了不影响剪切角度，同时增大L1与L2，取L1=960 mm，L2=1070 mm。

表4 作图法与数值法结果对比

本文仅给出4300 mm双边剪的计算结果（见表 5）。

同样可得到相应的剪刃轨迹（见图4）。

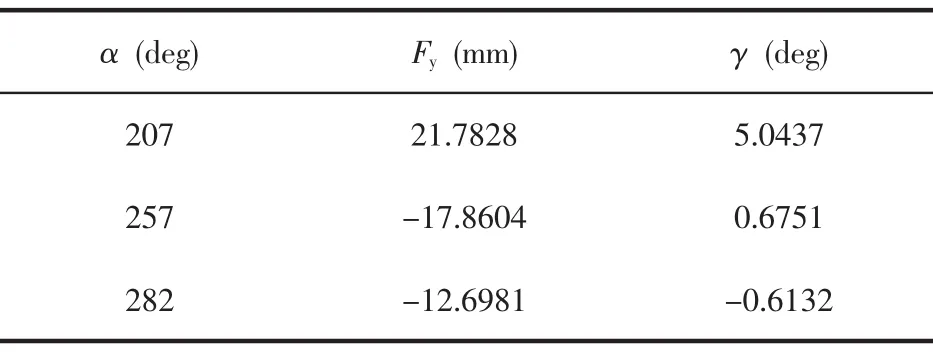
表5 数值法计算4300 mm双边剪剪刃不同相位时的Fy与γ

图4 4300 mm双边剪变连杆后上剪刃轨迹

图4中剪刃右端重合点在点16与17之间，重合段长度已大于1300 mm，此改变可以实现剪切薄钢板时步长1300 mm的要求，但因为剪刃最右点开口度已小于50 mm，剪切50 mm厚不能实现，对此可以通过改变剪刃上的倒角加以解决。

4 结语

（1）本文通过作图法及数值法对剪刃运动轨迹进行分析，建立起以双边剪曲轴偏心、连杆长度、剪刃圆弧半径等多变量方程式，改变方程中的任何一个结构参数都可以得到不同的剪刃运动轨迹。

（2）本文对剪刃轨迹方程进行了验证，证明了方程的准确性。

（3）本文仅对剪刃运动轨迹给出计算方程，利用本文方程可以实现剪刃轨迹在空间位置上的优化。

（4）本文的研究结果可做为剪切力及双边剪电机功率等的计算根据，也可以此结果为基础进一步开展双边剪结构研究与设计工作。