控制系统中基于映射云的不确定性表示
杨志晓 范艳峰
(河南工业大学信息科学与工程学院,河南 郑州 450001)
0 引言
控制系统存在着大量的不确定性,模糊性和随机性是其中最重要的两种[1]。不确定性主要来源于各种传感器、仪器仪表和执行机构的输出,也来自于输入量的细微波动以及温度、震动等各种环境因素。当输入量发生改变时,输出结果的不确定性特征可能发生改变。当前,控制系统一般将仪器仪表、执行机构的输出作为精确值处理[2-8]。不能阐述实际输出结果的不确定性及其可代表期望输出的确定程度,将给控制效果带来不可预知的风险。
云模型能够将定性概念的模糊性和随机性进行统一量化描述[9]。不过,云模型面向单个定性概念,它不能阐述仪器仪表和执行机构的输出不确定性在整个测度空间的变化情况。针对上述问题,本文提出云映射和映射隶属云的不确定性表示方法。其基本思想是分析关键输入量值输出的不确定特征,分别设计随机变量,实现输入到输出的非精确变换。同时,将不确定变换拓展至整个测度空间,定量表示输出不确定性及其在整个测度空间的变化情况。
1 云模型介绍
在自然界和人类认知过程的各种不确定性中,模糊性和随机性是最重要的两种不确定性。云模型能够将这两种不确定性进行统一量化描述。云模型由大量云滴构成。云滴可定义描述为[9]:假设U是用数值表示的定量论域,C是U上的定性概念,∀x∈U是定性概念C的一次随机实现;x对C的确定度用μ(x)表示(μ(x)是有稳定倾向的随机数,且满足 μ(x)∈[0,1]);x在论域U上的分布称为云,记为C(x),每一个x称为一个云滴。
在云模型的定义中,随机变量x不再是简单概率意义下的随机变量,而是对它的任何一个实现(即云滴x)都存在一个确定度μ(x)。μ(x)是云滴x能够代表定性概念C的程度,且确定度μ(x)也是一个有稳定倾向的随机数。确定度μ(x)的作用相当于模糊集理论中的隶属度,但它与隶属度最大的不同是它在给定随机变量取值下是一个随机数,而不是唯一确定值,从而将定性概念的模糊性和随机性统一起来。定性概念C的特征通过云的整体来体现,云滴的数量越多,云的整体特征越明显。
云模型用期望值Ex、熵值En和超熵值He这三个数字特征来表示,记为C(Ex,En,He)。期望值Ex是在论域U中最能代表定性概念C的点。熵值En既是定性概念随机性的度量,用来阐述云滴在论域空间的离散程度;又是定性概念模糊性的度量,能反映云滴在论域空间的集中程度。熵值越大,云滴越分散,集中度越低,概念更宏观;熵值越小,云滴越集中,概念的粒度更小、更清晰。超熵值He是熵的熵,He是熵值En的稳定性度量。超熵值越大,熵的稳定性越差。
自然界中的许多随机现象都符合正态分布,因此,云模型采用正态分布描述随机性,称为正态云[10]。即x~N(Ex,En'2),En'~N(En,He2)。x的确定度计算公式如下:

式中:μ为无量纲物理量确定度;x为实现的云滴;Ex为云的期望;En'为以熵值En为期望、以超熵值He为标准差实现的一个正态分布随机数。
根据已知样本(云滴)的统计特征,归纳云的数字特征值C(Ex,En,He),称为逆向生成云;若已知云的数字特征值,生成云滴,称为正向生成云。
2 云映射和映射隶属云
将仪器仪表、执行机构的工作过程看成是从输入到输出的一个映射变换,不失一般性,给出以下定义。
对非空集合A和B,若按照对应关系F,∀x∈A,存在随机变量Yx,在集合B上的值域为Ux⊆B,称F为A到B的一个云映射,记为,或 Yx=F(x)。
根据上述定义,集合A中的每一个元素∀x∈A,都通过一个随机变量Yx变换到一个可能的取值空间Ux⊆B。Yx的每一个取值在实现前都不能确定。对集合A中的全体元素,F定义了一个随机变量簇Y={Yx|x∈A}。各个随机变量的分布可能相同,也可能不同,其分布特征通过样本的统计特征进行估计。随机变量簇将集合A中的元素变换到一个云状不确定空间。F的特征通过全体随机变量簇Y来体现,因此,称F为云映射。
若A和B为定量值集合,对A中的若干关键元素,采用隶属云思想构造输出结果在这些给定输入值下的隶属云片。在集合A上对这些隶属云片的数字特征期望值、熵值和超熵值进行拟合,估计集合A到B映射F的期望函数、熵函数和超熵函数,从而构造F的隶属云。隶属云能够对整个有效输入范围内的输出及其不确定性进行定量表示,相关定义如下。
设Yx=F(x)为非空定量值集合A到B的一个云映射,∀x∈A,随机变量Yx在集合B上取得定量值域Ux⊆B。若Cx是定量论域Ux上的定性概念,∀y∈Ux是定性概念Cx在Ux上的一次随机实现,y对Cx的确定度μ(y)∈[0,1]是有稳定倾向的随机数,则 y在论域 Ux上的分布称为F在x处的一个隶属云片,记为C(Yx)。每一个y称为一个云滴。全体云片组成F的隶属云簇,称为云映射F的隶属云,简称映射云,记为C[F(x)]。
与单个定性概念的隶属云模型相比,上述定义将其拓展至云映射F的整个自变量空间A。集合A中的每一个元素x都对应一个定性概念Cx。其全体元素对应一个定性概念簇CA={Cx|x∈A}。它们可能是具有实际意义的概念,也可能是没有现实意义的抽象概念。∀Cx∈CA,定量论域Ux⊆B内最能代表Cx的点是随机变量Yx的期望值的点,记为f(x)。f(x)在集合A上即构成了云映射F的期望,即精确函数y=f(x)。Cx的每个随机实现即为云滴。Cx在定量论域Ux⊆B内的模糊性和随机性用熵度量,记为e(x)。云滴y能够代表定性概念Cx的确定度μ(y)是一个具有稳定倾向的随机数。其随机特征用超熵度量,记为h(x)。定性概念Cx的特征通过在x处的大量云滴构成的隶属云片的整体来体现。全体隶属云片能够反映概念簇CA随集合A中元素的变化情况。
在整个集合A上,f(x)、e(x)和h(x)分别称为云映射F的期望函数、映射隶属云C[F(x)]的熵函数和超熵函数。当∀x∈A时,定性概念C(x)的云数字特征为C[f(x),e(x),h(x)]。F的隶属云也可称为精确函数y=f(x)的云。它在本质上反映了以函数y=f(x)为期望的不确定性映射关系在值域空间和确定度空间的分布。对仪器仪表、执行机构的输入输出关系而言,其映射云反映了在给定输入下,输出的可能取值及实现的取值可代表期望输出的确定程度。
本文沿用文献[10]的正态云,即∀x∈X,y~N[f(x),En'2],En'~N[e(x),h2(x)],y的确定度可按照下式计算:

3 映射云算法
3.1 逆向映射云算法
在仪器仪表、执行结构的有效输入范围内选取关键点,分别重复设定输入量、测量输出值,以获取各输入量值下的多个输出样本,从而估计出在各关键点输出的期望值、熵值和超熵值。分别对它们在各个关键点的取值进行拟合,估计出期望函数f(x)、熵函数e(x)和超熵函数h(x)的过程,称为逆向生成映射云。该算法具体描述如下。
①在有效输入范围内随机产生M个均匀分布的值 X={xi|i=1,2,…,M};
②∀xi∈X,对输入、输出进行N次设定和测量,获得输出样本 Yi={yij|j=1,2,…,N};
③估计输出在xi处的期望值:

估计输出在xi处的熵值为:
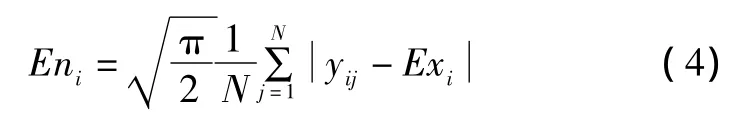
估计输出在xi处的超熵值为:
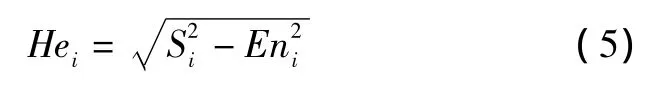
其中,
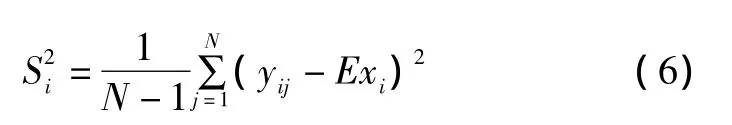
④ 分别对 M 对数据{(xi,Exi)|i=1,2,…,M}、{(xi,Eni)|i=1,2,…,M}和{(xi,Hei)|i=1,2,…,M}进行拟合,获得对期望函数f(x)、熵函数e(x)和超熵函数h(x)的估计。
3.2 正向映射云算法
根据输入-输出逆向映射云生成算法获得的映射隶属云C[f(x),e(x),h(x)],产生在给定输入值下的一个输出实现的过程,称为正向生成映射云。该算法具体描述如下。
① 输入x0∈A,分别由f(x)、e(x)、h(x)计算 F(x0)的期望值f(x0)、熵值En0=e(x0)、超熵值He0=h(x0);
② 由 En0'~N[e(x0),h2(x0)]产生 En0';
③ 由y~N[f(x0),En0'2]产生y;
④由下式计算确定度:
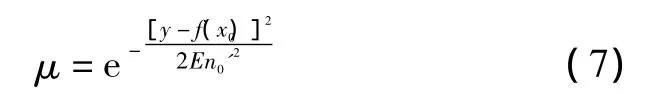
4 D/A卡的映射云
某D/A卡为12位,输出量程为电压0~5 V,则其输入量的数字量范围为000H~FFFH,对应的十进制数范围为0~4 095。输入与输出在理想状态下的关系可以表示为:

式中:x为介于0~4 095的无量纲数;y为输出的电压值,V。
在000H~FFFH之间等间隔地选取11个数字量作为输入量,分100次重复写入D/A卡,测量输出电压值。按照输入输出逆向映射云生成算法获得的期望函数同式(8)。
熵函数的估计为:

超熵函数的估计为:

式(9)和式(10)表示各输出在整个测度空间的熵和超熵值基本相同,也就是说在各输入量下,D/A转换得到的电压值的分布规律基本相同[11]。
根据逆向映射云算法获得的特征函数,运用正向映射云生成算法获得的映射隶属云如图1所示。

图1 输入-输出映射云Fig.1 Input-output mapping cloud
由图1可以看出,映射云模型不仅能够阐述D/A卡在给定输入值下其输出的模糊性和随机性特征,并通过确定度描述变换结果可代表期望输出的确定程度;而且还能够描述这种不确定性在整个测度空间的变化情况。
5 结束语
本文提出了云映射和映射隶属云的概念,对控制系统各种仪器仪表、执行机构的输出不确定性进行定量表示。云映射通过随机变量簇将精确值集合变换到各自可能的取值空间。在给定输入量值之后,采用隶属云模型建立输出的隶属云片。在有效工作范围内选取关键输入值,分别建立输出的隶属云片。根据各隶属云片的期望值、熵值和超熵值,估计输入输出映射关系在整个有效工作范围内的期望函数、熵函数和超熵函数,从而构造输入输出在整个有效工作范围内的映射隶属云,用来定量表示仪器仪表、执行机构输出结果的模糊性和随机性。以某D/A卡为例,说明了逆向隶属云的生成过程和采用正向隶属云表示输出不确定性及确定程度的有效性。
[1]李德毅,刘常昱,杜鹢,等.不确定性人工智能[J].软件学报,2004,15(11):1583-1594.
[2]李振华,王志新,张华强.分布式无线数据采集系统的实现方法[J].自动化仪表,2010,31(5):73-78.
[3]黄培.电动机监控系统的设计与实现[J].自动化仪表,2010,31(4):30-33.
[4]谷志新,王述洋,马雷,等.无线温度采集系统的设计[J].自动化仪表,2010,31(4):73-76.
[5]胡鹤鸣,王池,孟涛.多声路超声流量计积分方法及其准确度分析[J].仪器仪表学报,2010,31(6):1218-1223.
[6]佟庆彬,张晓冬,丁振良,等.基于激光视觉的石英摆片厚度精密测量方法[J].仪器仪表学报,2010,31(6):1358-1363.
[7]张久云,李世武.湿蒸汽流量仪检测与标定系统的研制[J].化工自动化及仪表,2010,37(6):35-38.
[8]李颀,栾翔鹤.智能阀门定位器的研究与开发[J].化工自动化及仪表,2010,37(4):64-66.
[9]李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究与发展,1995,32(6):15-20.
[10]李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.
[11]蒋伟,戴义保,何伟.基于ARM9的便携式测力仪设计[J].自动化仪表,2008,29(12):54-57.

