启发式动态规划在糖厂澄清工段pH值控制中的应用

宋春宁 王保录 周晓华，2

(广西大学电气工程学院1，广西 南宁 530004;广西工学院电子信息与控制工程系2，广西 柳州 545006)

0 引言

澄清工段是糖厂制糖过程中一个十分重要的生产工艺环节。澄清工艺中，将中和pH值和清汁pH值控制在要求的范围内是实现澄清技术优化的主要指标。该指标对于获得高质量的清汁和提高糖回收率有着重要作用。而澄清工段是一个复杂的非线性系统，具有非线性、多约束、时变大时滞、多输入等特点，这些特点对pH值的控制和澄清过程都有非常大的影响［1－3］。在分析糖厂澄清工段工艺流程和各种pH值影响因素的基础上，提出了一种利用模糊神经网络模型的自适应动态规划方法，从而解决了糖厂澄清工段中和pH值难以实现稳定控制的问题。

1 建立糖厂澄清工段模型

1.1 糖厂澄清工段工艺过程

目前，我国大多数糖厂的澄清工段采用的是亚硫酸法生产工艺。在这个工艺过程中，蔗汁的pH值是一个很重要的指标，它将直接影响白糖的产量和质量［1］。经过压榨工段得到的混合汁含有大量的杂质，如多糖、蛋白质、各种氨基酸与有机酸，此外还含有很多的蔗屑和泥沙，成分非常复杂。澄清工段就是尽量分离去除非糖成分，得到纯净的蔗汁，并取得较好的糖分收回率。

亚硫酸法澄清过程是一个复杂的物理化学过程，可分为预灰、加热、中和反应、沉降过滤四个阶段［2］。其过程流程如图1所示。

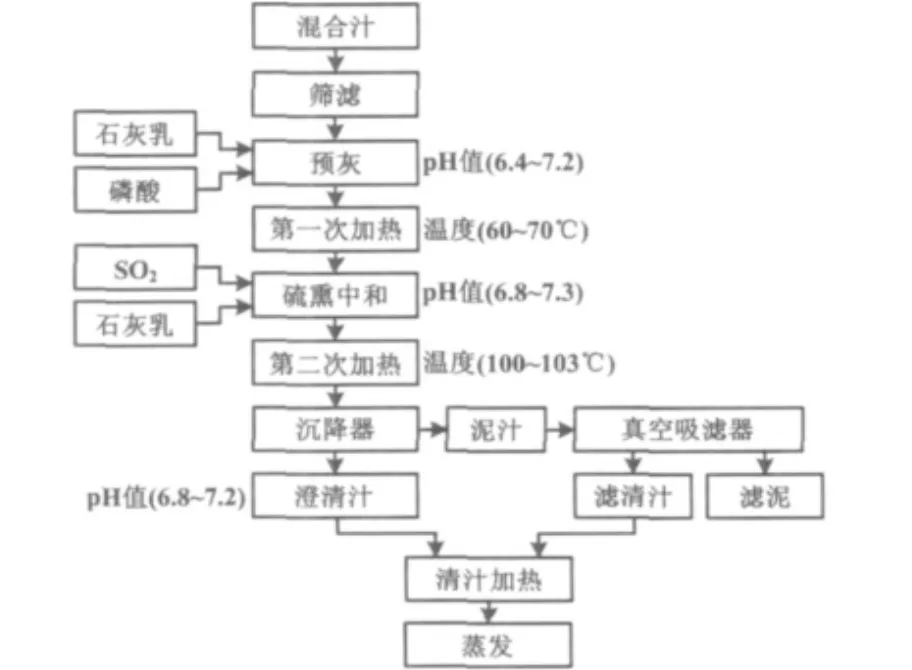
图1 蔗汁澄清过程流程图Fig.1 Flow process of clarification wrokshop section in sugar refinery

影响中和pH值控制的因素主要有以下几个。

①蔗汁流量不稳定将直接影响后续的操作控制，如加石灰乳、SO2和H3PO4等操作。

②预灰pH值偏高或偏低，将对硫熏中和控制造成困难。

③石灰乳、SO2流量的影响。加入石灰量和SO2量过少或过多，则会使中和反应不完全，使清汁中残留的钙盐增加，导致轻质纯度下降。加入石灰量过多或硫熏不足，会导致蔗汁中还原糖的分解，清汁色值升高、纯度降低。

上述是几个客观存在的影响因素，控制好这几个因素是稳定中和pH值的关键。

1.2 模糊神经网络模型

建立糖厂澄清工段模型主要有两方面作用:①作为启发式动态规划(heuristic dynamic programming，HDP)控制器的被控对象;②作为HDP控制器的模型网络部分。在工业运行数据中，包含反应输入条件及操作参数与工艺指标之间关系的信息。在处理和解决问题时，模糊神经网络不需要给出对象的精确数学模型，它通过改变网络结构，逐步适应外界各种影响因素的作用，在高度非线性和不确定性的系统建模方面具有很大的潜力［5－7］。

根据糖厂澄清工段工艺机理分析，影响中和pH值这一工艺指标的因素主要包括甘蔗榨量、蔗汁流量、预灰pH值、一次加热温度、硫熏强度、加灰量和二次加热温度等参数。因此，本文设计的模糊神经网络结构如图2所示。

图2 模糊神经网络结构Fig.2 Structure of fuzzy neural network

模糊神经网络模型对于非线性问题具有较强的拟合能力，但对于大时滞、参数分布和时变性等存在复杂的工业过程，特别是训练的样本数据不足时，仅依赖于模糊神经网络模型很难达到模型精度的要求。在正常的生产条件下，基于大量的工业运行数据建立的模糊神经网络能够很好地描述这一生产过程。而工况的判断需要通过历史数据获得，令样本数为M，某输入变量xi的取值区间为Q，将Q分为m个子区间{Q1，Q2，…，Qm}，由于大多数样本是在生产正常的情况下获得的，故可认为某个子区间的样本越多，其工况越正常。因此，根据各子区间所包含的样本数占总样本数的比例，糖厂澄清工段的工况归纳为以下三类。

其中，εmin和εmax是根据经验确立的样本比例参数，在实际的工业生产中，正常的区间只有一个。输入量的模糊隶属度函数如图3所示。其中 a2min、a1min、a1max和 a2max可通过历史数据统计获得，在 ［a1min，a1max］内，工况正常;在(a2min，a1min)及(a1max，a2max)内，工况比较正常;其余范围都属于异常。由此可定义输入变量xi的模糊论域为Ex，Ex表示适用模糊神经网络模型处理的范围。Ex的隶属函数形式为:

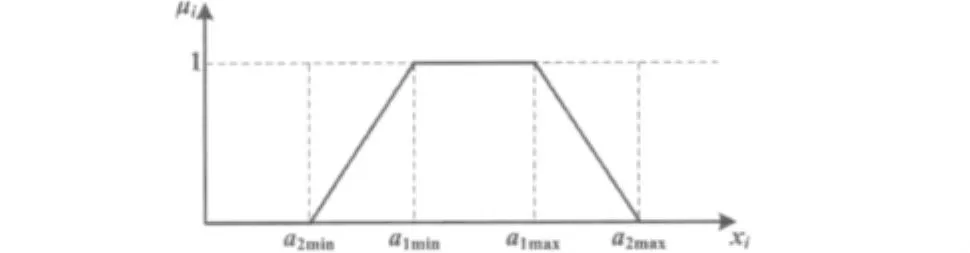
图3 输入量的模糊隶属度函数Fig.3 Fuzzy membership functions of input

采用加权法计算模型的权重为:

式中:μi分别为模糊神经网络中r个输入变量的隶属度;βi为隶属度权系数，满足0＜ βi＜1且 β1+β2+…+βr=1，βi表示输入变量对模型预测结果的影响程度，可通过对历史数据的统计结果得到。

1.3 模糊神经网络模型训练及仿真

建立的糖厂澄清工段模型只有具有足够的样本数据，才能反映出系统的内在特性。根据采集的广西某糖厂澄清工段1 000组实时数据的输入输出关系，可以采用神经网络建立其模型。部分实时数据如表1所示。

式中，X1，第一主成分变量；X2，第二主成分变量。将标准化后的反应速率常数k2与X1和X2之间建立多元线性回归模型，得到的回归模型如式(5)所示：

表1 某糖厂澄清工段部分实时数据Tab.1 Partial real-time data of the clarifying workshop section in certain sugar refinery

将网络的结构、样本数据作预处理和归一化后，在Matlab7.0环境下，采用 Levenberg-Marquardt算法对网络进行训练，得到糖厂澄清工段模糊神经网络模型的训练曲线如图4所示。

图4 训练曲线Fig.4 Training curves

2 HDP控制器的设计

2.1 自适应动态规划(ADP)原理

自适应动态规划(adaptive dynamic programming，ADP)是指所有在扰动或不确定条件下随时间变化的最优化神经网络设计，目的是近似贝尔曼动态规划方程中的代价函数(cost-to-go)，从而避免“维数灾”问题［8－9］。其基本思想是通过估计代价函数(cost-to-go)(或/和代价对状态的微分函数)来避免每个阶段内针对所有状态和控制变量进行精确计算，并通过与实际或仿真系统的相互作用来减少对模型的依赖性，提高上述估计的精度，从而更好地指导最优(次优)策略的求取。自适应动态规划典型结构包含评价网络、模型网络和执行网络三部分［10］。根据评价网络输出的函数不同，现有的自适应动态规划方法主要有三种类型:启发式动态规划HDP、双启发式动态规划DHP和全局双启发式动态规划(global dual heuristic dynamic programming，GDHP)［11－12］。本文将使用 HDP 方法来控制糖厂澄清工段中和pH值。

2.2 HDP控制器的基本结构

HDP控制器结构如图5所示，它由评价网络、模型网络和执行网络三个基本模块组成，每个网络模块都包含有前馈单元和反馈单元［10－13］。

图5 HDP控制器结构图Fig.5 Structure of the HDP controller

图5中，实线表示信号流向，虚线表示调整评价网络和执行网络参数的反向传播路径。执行网络接收系统的状态参数x(t)，产生当前状态下的控制信号u(t)，u(t)与系统当前状态参数x(t)一起送入模型网络;由模型网络预测新的状态x(t+1)，x(t+1)信号作为评价网络的唯一输入信号;最后评价网络输出J函数的近似值。受控对象为糖厂澄清工段模糊神经网络模型，它既作为控制器的被控对象(或受控系统)受到执行网络输出的控制信号u(t)的控制，也作为模型网络预测新的状态参数x(t+1)。此外，图5中的U(t)为效用函数，γ为折扣因子，Z－1为延迟环节。

2.3 评价网络的训练

评价网络的输入仅为模型网络预测输出的受控系统的状态参数x(t+1)。由于系统的状态参数只有中和pH值这一个量，所以评价网络的输入也只有一个量。令评价网络的输出为代价函数J，HDP的中心思想是训练评价网络，以近似贝尔曼最优化方程中的代价函数J:

式中:γ为折扣因子，取值范围是［0，1］，在此取0.95;U(t)为效用函数，用于给控制对象发出控制信号。在工业生产中，U(t)的选取决定了动态优化控制的优劣。因此，为设计满足系统要求的优化控制器，U(t)必须能够反映控制系统中各种各样的问题。考虑到不同的控制问题效用函数的形式也是不同的，本文的控制对象是糖厂澄清工段中和pH值，目标是将中和pH值稳定在7.0～7.4，因此选择的效用函数如下:

式中:X(t)为中和pH值;U(t)为效用函数。

采用评价网络输出代价函数J，使下面的误差函数达到最小:

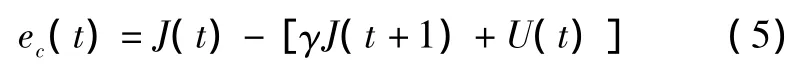
评价网络的最小化目标函数为:

采用式(6)所示的最小化目标函数作为训练目标，可以训练一个评价网络。采用梯度下降法，其权值的更新规则满足以下公式:

式中:lc为评价网络学习率，它是一个大于0小于1的数;γ为折扣因子;wc为评价网络的权值。

2.4 执行网络的训练

执行网络是HDP控制器的执行者，其获得系统的状态参数后，执行网络输出的控制信号不仅要改变系统的状态，还要与当前系统的状态参数一起送入评价网络，由评价网络对其控制作用作出相应的评价。

执行网络的训练最终是要确定权值矩阵Wa1和Wa2的值。与评价网络训练不同，执行网络的训练目标是最小化评价网络输出的代价函数J。通过评价网络的输出误差，并经过评价网络反向传播到执行网络来更新执行网络的权值，其算法如下:

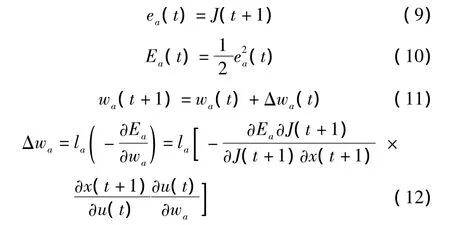
式中:la为执行网络的学习率;wa为执行网络的权值。

2.5 模型网络的训练

模型网络直接采用糖厂澄清工段的模糊神经网络模型，因此，其模型是确定的，不需再作训练。

3 模拟试验结果分析

利用澄清工段pH值模拟试验装置分析试验结果，样汁在反应罐中与中和液中和，经pH值检测槽流到存储罐进行加热。玻璃电极置于检测槽内，测量中和后的混合汁pH值。本试验采用的样汁pH值为6.5，碱液的pH值取12.27。pH值中和过程控制的目标是使中和pH值为7.2，得到的中和pH值控制曲线结果如图6所示。

图6 中和pH值控制曲线Fig.6 Control curve of the neutralization pH value

从图6可以看出，混合汁pH值从6.5上升到7.2的过程中，pH值的上升速度很快，且超调量较小。在18:03时，向反应罐中加大碱液的流量会造成剧烈的干扰。当遇到剧烈干扰时，系统的反应速度非常快，能够使pH值迅速回到目标值。

4 结束语

在系统地分析糖厂澄清工段工艺流程的基础上，基于模糊神经网络模型和HDP控制器，构建了模糊神经网络模型。试验表明，系统取得了较好的控制效果。

［1］陈维钧，许斯欣.甘蔗制糖原理与技术第二分册-蔗汁清净［M］.北京:中国轻工业出版社，2001.

［2］Blackwell J.Recent developments in the sugar industry［J］.International Sugar Journal，2001(102):43－60.

［3］Beck K，Peters L，Papur P，et al.Application of soft-computing techniques in optimization and control of complex processes in sugar industry［J］.International Sugar Journal，2002，1245(104):390－400.

［4］霍汉镇.低温磷浮法——21世纪的制糖新工艺［J］.广西轻工业，2001(1):21－26.

［5］周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京:清华大学出版社，2005.

［6］李国勇，智能控制及其MATLAB实现［M］.北京:电子工业出版社，2005.

［7］张德丰.MATLAB神经网络应用设计［M］.北京:机械工业出版社，2009.

［8］黄伟，魏镜搜，王庭有，等.模糊智能控制在磨矿分级系统中的应用研究［J］.昆明理工大学学报:理工版，2009，34(4):96－100.

［9］于军琪，吴涛，黄永宣，等.磨矿分级系统溢流浓度的模糊智能控制［J］.西安交通大学学报:自然科学版，1999，33(9):1－9.

［10］Werbos P J.Stable adaptive control using new critic designs［EB/OL］.［2011 － 09 － 18］.http://arxiv.org/abs/adaporg/9810001v1.

［11］Prokhorov D V，Wunsch D C.Adaptive critic designs［J］.IEEE Transactions on Neural Networks，1997，8(5):997－1007.

［12］Paul J.Tutorial on neural control，control theory and related techniques:from back propagation to brain-like intelligent systems［C］∥12th ICMCM ＆ SC，1999.

［13］Liu W X，Venayagamoorthy G K，Wunsch D C.A heuristic-dynamicprogramming-based power system stabilizer for a turbogenerator in a single-machine power system［J］.IEEE Transactions on Industry Applications，2005，41(5):1377－1385.