呼叫中心排班优化模型的研究
徐迅羽,杨根科
0 引言
呼叫中心是企业与客户交流的重要环节,它能使企业降低成本,提高效率,根据McKinsey公司([1],2006)的报告显示,在某些行业中,呼叫中心甚至可以给企业带来25%的收入,而排班问题是呼叫中心的核心问题。Aksin ([2],2007)对排班问题近年来的研究进行了全面的回顾,内容包括了排队论,模型的仿真以及优化算法。排班问题的输入一般由话务量和话务员服务时间的预测结果得到[3],Mandelbaum([4],2006)对呼叫中心排队模型的分析表明最常规的排队模型仍然是ErlangC模型。对于话务员人性化管理,Fukunaga([5],2002)的研究考虑了话务员指派问题中将话务员的意愿作为目标函数的一部分。Koole([6],2003)研究了在全局服务水平满意约束下排班问题多目标算法设计。Gans([7],2003)在其研究中讨论了以服务质量和排班效率作为指导的排班体制。Atlason([8],2004)研究了降低话务员上班成本与满足服务水平的多目标问题。Thomas([9],2010) 研究了排班问题的随机模型,将排班成本以及服务能力不足造成的经济损失同时作为优化目标函数的排班问题。对于排班问题算法,Cezik([10],2006)用线性规划模型对其求解.Saltzman([11],2005)([12],2007)将线性规划和禁忌算法相结合来对目标函数进行求解。Athanassions([13],2009)应用了随机化方法与整数规划相结合的算法。
1 排班问题的仿真模型
由于客服的行业特征,排班方案会涉及到许多因素,影响到顾客,管理者和话务员的三方利益。在仿真模型中充分考虑到影响因素,并将模型分成班次设计和班组指派两个子模型,使排班问题更具有层次性和实际操作性。
1.1 给定的输入条件
1.1.1 班次种类及其喜好度的描述
T1,T2,T3——早中晚班最早开始时间。早班:起始时间∈[T1,T2);中班:起始时间∈[T2,T3); 晚班:起始时间∈[T3,T1);λ1,λ2,λ3,0——分别表示早班、中班、晚班和休息班产生的喜好度;
1.1.2 疲劳度参数
D(s,t)—— 话务员的精力状态与服务质量有着密切的关系,在任何时间段上提供一个相对稳定的服务质量是考核呼叫中心服务水平的重要指标之一。而和话务员精力密切相关的是话务员在每个时间段上的疲劳度。
根据对话务员疲劳度的研究显示,话务员的疲劳度主要和两个因素有关:班次的种类s和当天累积上班的时间t。本文中,假定话务员班次种类分成早班,中班,晚班和休息班,它们各自对应的累积疲劳度D(s,t),如表1所示[15]:

表1 累积疲劳度值D(s,t)的统计量
1.1.3 班组意愿约束(硬条件,软条件)
为了更好的体现呼叫中心排班策略的人性化,排班策略将话务员的意愿纳入了排班考虑因素。话务的意愿分为硬条件(H,H´)和软条件(S,S´),硬条件表示一定要满足的意愿,软条件表示尽量要满足的意愿。
H——表示i天,k班组意愿的硬约束和软约束;

1.1.4 轮换规则
呼叫中心为了更人性化的进行排班计划,除了对具有硬条件意愿的班组进行特别排班外,其他班组需要遵循轮换规则
R——轮换规则的集合(当前班与后续班),考虑到劳动法等因素,得到所有可行的当前与后续班次的轮换规则:
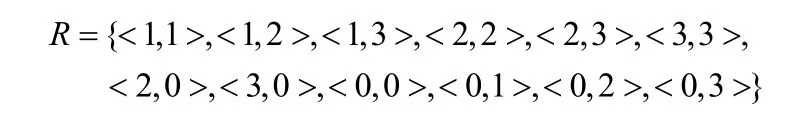
1表示早班,2表示中班,3表示晚班,0表示休息
1.2 决策变量、计算变量与约束描述
1.2.1 有关班次设计的变量描述
此部分对班次进行设计,未和实际班组进行配对,其主要涉及到服务水平和排班成本等相关因素

前3个约束表示4个决策变量必须在正确的时间段中;后四个约束分别表示班次覆盖时间长度,表示连续工作时间长度和中间休息时间长度必须在规定的上下限中。
考虑到影响因素和表示方便,引入以下计算变量:
f1(i,j,l)——表示在i天,j班次,l时段是否在上班
f2(i,j)——表示在i天,j班次覆盖的上班时间长度
f3(i,j)——表示在i天,j班次所上班的类型
f4(i,j,l)——表示在i天,j班次,l时段已经上了多少时间的班
f5(i,j)——表示在i天,j班次的种类产生的喜好度
f6(i,l)——表示在i天,l时段设计有多少班次上班
f7(i,j,l)——表示i天,j班次,l时间段上产生的疲劳度
f8(i,l)——表示在第i天第l个时间段上话务员的平均疲劳度值
由以上变量可以建立相关的计算关系如下:

其中1表示早班,2表示中班,3表示晚班,0表示休息

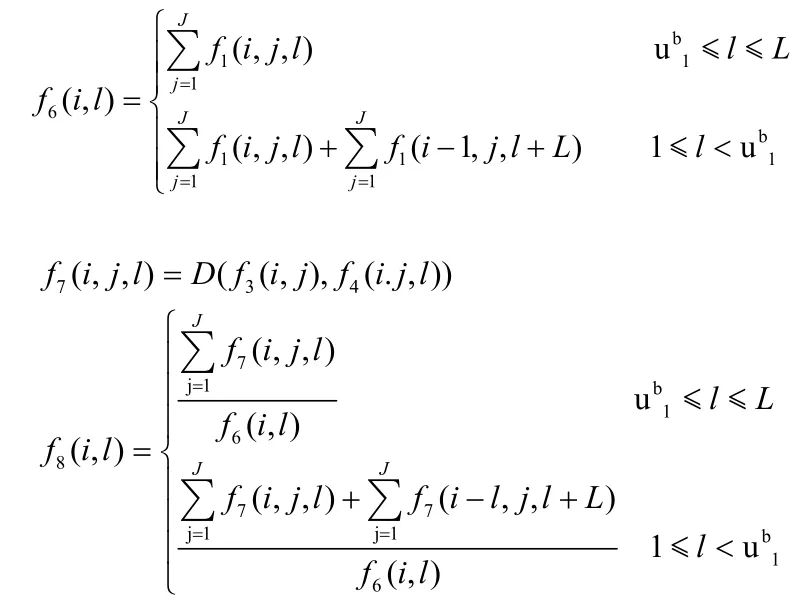
1.2.2 有关班组指派的变量描述
此部分将设计好的班次与实际班组进行配对指派,其主要涉及到话务员的利益因素。
Yk,i,j——表示i天,k班组是否被指派上j班次的班取值约束:

此约束表示一个班组每天只能被指派到一个班次上考虑到影响因素和表示方便,引入以下计算变量:
g1(k,i)——表示i天,k班组所上班的类型
g2(k,i)——表示i天,k班组的软条件是否被满足
g3(k)——表示班组k喜好度的总和
g4(k)——表示班组k总工作时长
rk——表示班组k当前与后续两个班次的轮换安排
由以上变量可以建立相关的计算关系:

1.3 约束条件:
在这个环节中的约束条件有三部分组成,客观条件约束,班组意愿约束和轮班规则约束
1.3.1 客观条件约束

以上第一个约束表示各个时间段的班组数量必须小于呼叫中心容量上限。第二个约束表示总工时必须在总工时的上下限之间;
1.3.2 班组意愿约束

前两个约束表班组每天只能提出一个意愿;后两个约束表示班组提出的硬条件意愿必须被满足;
1.3.3 轮班规则约束
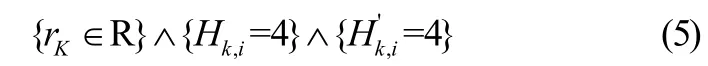
这个约束表示没有硬条件意愿时必须满足轮换规则;
2 班次设计优化模型
2.1 指标设计
在此部分,我们考虑客户服务满意指标、经济指标和服务质量指标在分别满足客观约束条件下的最优:

2.1.1 客户服务满意指标
当设计的班次数量小于预测班次数量的时候,会导致实际服务水平达不到期望值,直接影响到客户接受服务时候的满意程度。单位时段上班次平均短缺程度描述如下:

2.1.2 经济指标
当预测班次数量小于设计班次的时候,产生多余的人力成本,企业利益受损,单位时段上班次平均冗余程度描述如下:

2.1.3 服务质量指标
呼叫中心希望每个时间段上话务员的平均疲劳度值保持平衡,以呈现一个平稳的服务质量,平均疲劳度值的方差如下:

2.2 班次设计的算法---PSO
2.2.1 PSO算法的介绍
该算法模拟鸟集群飞行觅食的行为, 通过鸟之间的集体协作使群体达到最优目的,基本原理为:
一个由q个粒子组成的群体在D维搜索空间中运动,第i个粒子的位置与速度表示为(xi,vi),1≤i≤q. 第i个粒子经历过的最好点表示为pi,群体内所有粒子所经过的最好点表示为pg,粒子的位置和速度根据如下方程进行变化[16]:
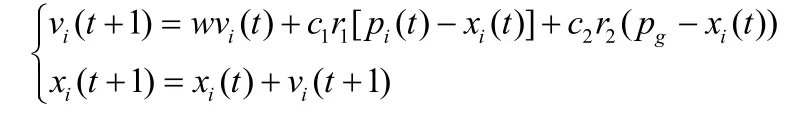
w是惯性因子,使粒子保持惯性和搜索趋势;c1和c2是非负常数,称为学习因子;r1,r2~U(0,1)的随机数[17]
2.2.2 粒子的设计
一个班次的确定由两部分组成,班次起始时间和班次的作休类型(比如工作3小时休息1小时再工作4小时都归为一种作休类型)。假设根据约束条件,共有M种可行的班次作休类型,对一个粒子设计如下:
一个粒子为K维,每一维取值Z,Z∈[1,M*L]。每一维数值Z就可以提供2个信息,班次起始时间Xi,j,1和班次类型m。起始时间取值为(Z/M)的余数,班次类型取值为(Z/M)向上取整,以此确定一个班次。
2.2.3 改进点
由于此问题的峰值较多,变化率较快,在原有的PSO算法上进行了一些改进:
(1) 由于此问题中K种班次有很多种组合可以逼近最优解,在整个可行域上有许多峰值,所以所有粒子向全局最优gbest进行学习后,会导致粒子都向gbest收敛,形成局部最优,不利于全局搜索,在此,本文借鉴了“CLPSO”[18],粒子将不学习Pg的值,而是会有一定概率Pc去学习其他粒子的最优值Pi,这样增大了此算法的全局搜索能力。
(2) 由于此问题是一个高维问题,考虑到在一些适应度较差的粒子中,存在着部分优质维数信息,但是却因为其适应度较差而没有被学习到。为了避免这种情况,在本文借鉴了“A-CLPSO”[20]算法中让一定数量的粒子去学习适应度较差的粒子(数量为n1),以此跳出局部最优来寻找全局最优。
(3) 由于开始的时候是随机成成粒子,此问题的峰值较多,会容易形成一些适应度很差的班次组合,这些粒子容易出现在较差的局部最优,甚至在互相学习中有害于其他粒子。为了避免这种情况,在本文借鉴了“A-CLPSO”[20],算法中设置最差的一些数量的粒子进行自身变异(数量为n2),从而获得更好适应度的粒子。
3 班组指派优化模型
3.1 指标设计
班次指派阶段是将企业中具体的工作班组指派进前一部分设计好的班次中。前一部分中,企业管理者对于客户满意指标、经济指标、服务质量指标等指标进行了讨论,而这些指标通常在排班问题中具有较高的优先级。而在本环节中,班组指派的指标考虑了话务员排班喜好度的平衡性,总工时的公平性以及话务员排班意愿的满足度得到最优。
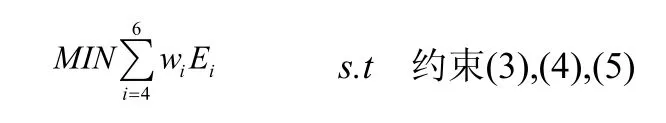
3.1.1 班组排班喜好度的平衡性
喜好度指班组在被指派到不同种类的班次的时候产生的对此类班次的喜好程度,在指派过程中,我们希望班组之间被安排到的班次的总喜好度尽量接近,减少班组对排班结果的不满情绪。喜好度总和的方差如下

3.1.2 总工时的公平性
总工时公平性表示话务员之间被安排到的班次的总工时数应当尽量接近。总工时的方差如下

3.1.3 班组排班意愿的满足度
在班组指派中,企业都会考虑班组的意愿,本文中将话务员的意愿分成两种:硬约束和软约束。硬约束表示一定要满足的条件,软约束是可满足可不满足的条件。作为企业的管理者,尽可能满足意愿是排班评估的重要指标之一,累计如下:

3.2 班组指派的算法—旋转排班法(shifting scheduling)
在此阶段,约束条件有班组意愿(硬约束),劳动法限制,轮换规则等,指标有总工时公平性,喜好度公平性,意愿满足程度。旋转排班法在满足约束条件的情况下,根据3个指标不同优先级来进行班组指派活动。一天的旋转规则如下:
第一步,将拥有硬约束意愿的班组首先指派,满足硬约束意愿。
第二步,检查是否有班组达到连续工作日的上限,发现则指派休息班组。
第三步,根据总工时公平性,总喜好度公平性,班组意愿满足程度的优先级条件对未指派班组进行排序,依次根据轮班规则进行指派,尽可能满足话务员软条件的意愿。发现没有满足轮班规则的班次时,此班组指派为休息班。
第四步,未被安排到的班组指派为休息班。
第五步,统计总工时,总喜好度,连续工作日长等参数。
利用旋转排班法,我们最终可以得到排班表。
4 规划调度参数的反馈调整策略
由于排班结果不能一次达到理想效果,本文中将对规划调度参数的调整引入反馈回路中,通过修正规划调度参数,获得最终排班表。而能够被调整的参数和作用如下:
Ptsf, TAW——调整预测统计部分的指标值,改变排班部分输入参数,影响排班结果整体的服务质量指标;
ub,lb——调整班次设计部分的约束条件,改变班次的多样性,影响班次设计部分的指标E1,E2,E3;
优先级pr——调整班组指派指标(喜好度的平衡性,总工时的公平性和意愿的满足度)的优先级pr,影响E4,E5,E6的优化程度;
[wi]——调整指标值的权重系数,改变各个指标被重视的程度,影响整个排班指标的输出;
5 仿真模型验证与仿真分析
5.1 仿真实例分析
5.1.1 仿真参数确定
基本参数:{I,L,Q,K,N}={7,24,150,100,5};时间节点{T1,T2,T3}={4,12,20};喜好度{λ1,λ2,λ3}={3,5,8};
5.1.2 预测部分
根据某电信中心的话务数据与管理情况,确定预测部分的参数[19]:
平滑常数α1=0.3,α2=1,β=0.2,平均服务时长u=240s,服务水平Taw=20s内接通率需要达到Ptsf,根据行业要求和黄金感官理论[14],每个时段上设置的最低拨通率取值在70%~85%,如表2所示:

表2 话务量以及班组数预测数据表[19]
根据话务数据和预测模型,此部分我们得到本期各时段的预测话务量和满足服务水平所需的最小预测班组数量Fi,l,如图2所示:

图2 预测话务量与预测班组数量曲线图
5.1.3 班次设计部分
班次设计的取值约束参数如下:

根据约束条件,得到班次作休类型的数量M=13(包括休息班),如表3所示:
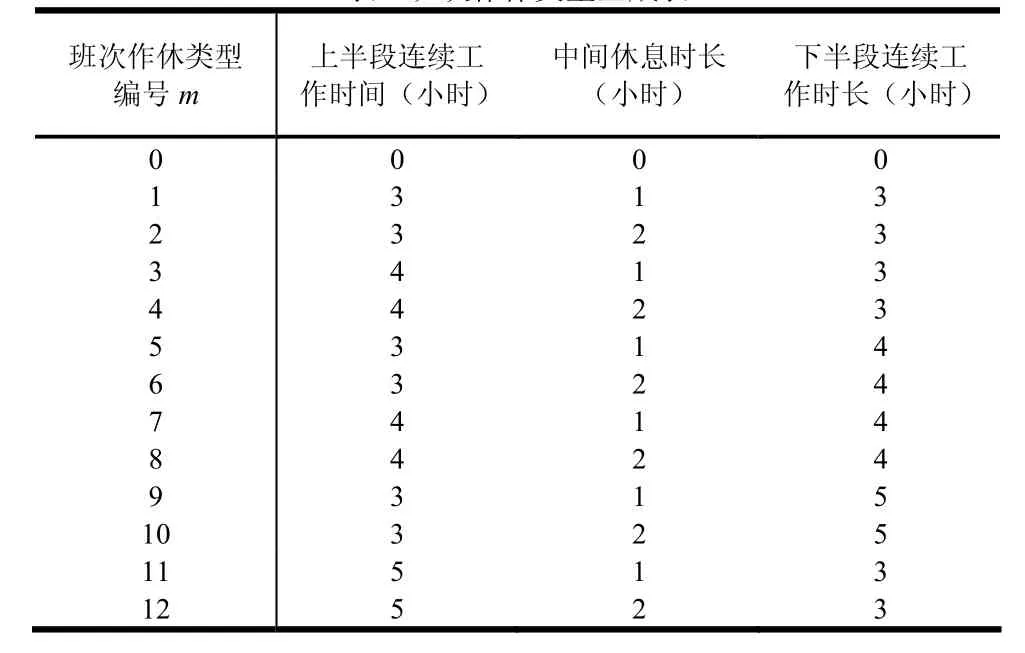
表3 班次作休类型生成表
然后利用PSO算法进行求解,PSO的参数定义,粒子数为30个,循环次数1000次。假设3个目标函数权重各占1/3,可以得到每天班次设计的结果(如表4班次行所示,详细数据见附录2),并由此得到每个时段上的实际拨通率与平均疲劳度值,如图3所示:

图3 实际拨通率与平均疲劳度曲线图
由图3可见实际拨通率与设置的最低拨通率有较好的拟合,平均每个时段上的差值在1%左右。而平均疲劳度值每天有周期性的变化,其主要维持在[1.7,2.2]区间内,不同时段的疲劳度值差值较小,以此体现呼叫中心在任何时段都拥有平稳的服务质量。
此时,得到班次设计部分的指标值为:E1=0.27,E2=0.31,E3=1.8。
5.1.4 班组指派部分

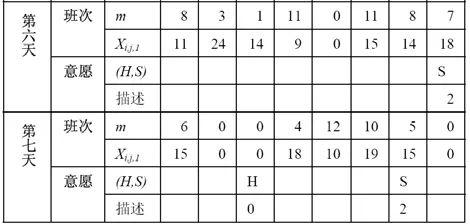
表4 班组一周排班表(前八组)
?
然后根据总工时公平性,总喜好度公平性,话务员意愿满足程度优先级排序(此处假设从高到低),将设计部分得到的班次结果与班组进行配对,得到最终排班。前八组班组的排班表如表4所示,其中参数对应如下:班组编号k,作休类型m,起始时间Xi,j,1,意愿类型(H,S),意愿描述(全体班组数据详见附录2)。
此处得到指派部分的指标值:E4=8.564,E5=13.091,E6=6。
每一组班组只需要根据排班表中有关他们的那一列进行上班即可。
5.1.5 仿真结果统计与评价
此次排班结果的全体班组统计数据:
各天上班班组数量:{76,69,64,63,74,70,79};一周各个班组种类数量:早班240组,中班180组,晚班93组,休息班187组(休息班比例为26.7%);一周硬条件意愿52个,软条件意愿27个;话务员平均一周工时数38.24小时;
相关指标经过计算可以得到,为了得到更直观的表示并且与其他文章比较,对各个指标设置最大值以及进行归一化和取反处理,得到优化百分比如下:
1) 客户满意度(平均短缺度):E1=0.81,平均每个时段上短缺0.81个班组,最大值取5,优化百分比为83.8%。
2) 经济成本(平均冗余度):E2=0.93,平均每个时段上冗余0.93个班组, 最大值取5,优化百分比为81.4%。
3) 疲劳度平衡性:E3=1.8,每个时段上平均疲劳度值的方差为1.8,最大值取10,优化百分比为82%。
4) 喜好度公平性:E4=8.564,班组总喜好度的方差为8.564,最大值取50,优化百分比为82.7%。
5) 总工时公平性:E5=13.091,班组总工时的方差为13.091,最大值取50,优化百分比为73.8%。
6) 班组意愿满足度:E6=6,共有6个班组软条件意愿没有被
满足,最大值取软意愿总数27,优化百分比为78%。
由排班结果可以看出,此排班方法在较大程度上拟合预测班组数量,保证顾客满意和成本控制的同时,兼顾到了话务员的感受因素,在博弈中得到预期的结果。
排班结束之后,可以得到最终排班表,和相关参数。管理可以根据得到的数值对排班结果进行评估,调整排班时候的策略,进行再次排班,直至得到满意结果。
5.2 仿真模型应用分析
上述实例分析验证了仿真模型的可行性,此部分根据以上实例数据,改变部分参数来验证本文仿真模型实际应用的可行性和适应性。
5.2.1 搜索最优班组数量
呼叫中心班组数量主要影响到班次设计部分的3个指标,如图4所示:
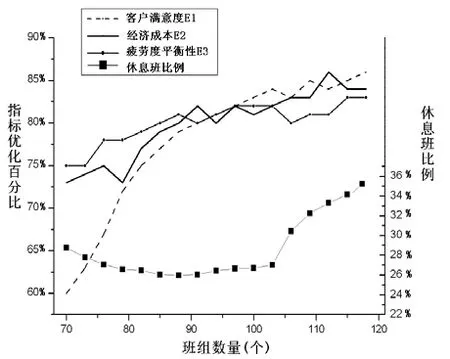
图4 优化指标与班组数量关系图
班组数量超过100时,3个指标随着班组数量上升有明显提高,但是休息班比例也有显著上升,说明此时排班结果的改善伴随着班组利用率降低的负面影响。当班组数量低于90时,3个指标随着班组数量减少而快速下降,经济成本即班组短缺率下降明显,而休息班比例上升的原因是排班约束保证班组必须的休息安排而班组总数下降导致比例上升。可见在以上实例中的呼叫中心的规模下,90组到100组班组是最适合的。由此验证此仿真模型搜索最优班组数量的可行性。
5.2.2 各方利益博弈选择
在呼叫中心规模一定的情况下,不同行业或不同的管理者对于各种指标有着不同的侧重性。以下对于本文仿真模型进行权重侧重性的改变来验证其对管理者排班要求的适应性,如表5所示:
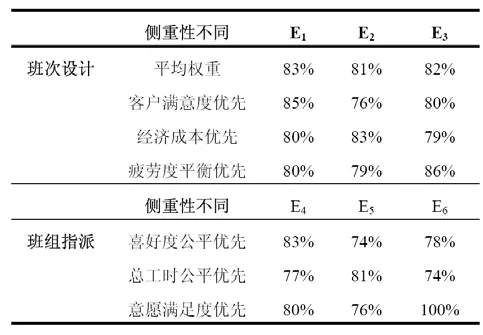
表5 不同权重下优化指标参数表
根据上表数据,显示本文仿真模型在改变指标权重的情况下,根据各方利益的博弈选择,得到不同效果的排班结果来满足不同的期望需求,验证了此仿真模型的普遍性和可行性。
5.3 仿真模型比较分析
根据与以前的研究进行比较[7][9],以前的研究主要考虑服务质量,排班效率和排班成本作为排班指标。而本文考虑更多的指标因素,包括班组意愿和疲劳度等,增加了问题复杂性,无法用以前研究中的线性规划和整数规划来求解,而本文的排班模型对现代呼叫中心排班问题也有更广泛的适应性。Thomas([9],2010)在对排班问题建模时考虑了服务水平与排班成本之间的博弈,将上述数据利用Thomas的排班问题进行求解,并且与以上实例比较,如图5所示:

图5 优化百分比对比图
Thomas对于客户满意度和成本控制有较好的效果,但在兼顾疲劳度,喜好度公平性与总工时公平性效果不佳。通过比较,说明本文的排班模型兼顾了更多的考虑因素,在博弈中寻找满足要求的排班结果,具有更广泛的普遍性和适应性。
6 总结
本文通过对呼叫中心排班问题的研究,引入了话务员的服务水平,呼叫中心成本的控制,话务员疲劳度,排班结果的公平性(总工时数等),话务员对排班结果的喜好(软约束,硬约束)等多样化的目标因素,建立排班问题的优化决策模型和相关的约束条件。在服务参数预测模型中引入话务到达时间随机变量、服务时间随机变量和最低拨通率随机变量等随机变量得到满足服务水平的班组数量。又由于客服需求曲线的随机性,话务员精力状态与服务质量模糊相关性,服务水平和话务员权利或者值班满意度的矛盾约束等的复杂性,依据对外的规划经营和对内的管理调度的不同,将排班问题分为班次设计与班组指派两个子模型,分别利用PSO算法与旋转排班法求解,得到排班表与相关参数。本文最后提出进一步采用反馈控制的理念,把管理者置于多目标决策问题的反馈回路中,通过修正各种规划调度参数,获得最终排班表诚然,这篇文章还有很多可以改进的地方,在文中假设班组都是单一技能,单一话务类型,实际呼叫中心可能有多种话务人员,这将是下一步可以研究的方向。之后,还可以找寻更大规模的实例,来测试在大规模需求中排班方法的性能。
[1]Eichfeld, A., T. D. Morse, K. W. Scott. Using call centers to boost revenue[R]. The McKinsey Quarterly. 2006.2
[2]Aksin, Z. The modern call-center: A multi-disciplinary perspective on operations management research[J]. Production and Operations Management .2007.16 (6):665–668.
[3]Weinberg. J. Bayesian forecasting of an inhomogeneous poisson process with applications to call center data[J]Journal of the American Statistical Association, 2007.102,1185–1199.
[4]Mandelbaum, A. Service-engineering of call centers:Research, teaching, practice[B].IBM Business Optimization and Operations Research Workshop, Haifa, Israel.2006.3
[5]Fukunaga, A. Staff scheduling for inbound call centers and customer contact centers[J].Eighteenth National Conference on Artificial Intelligence, 2002.822–829.
[6]Koole, G. Optimal shift scheduling with a global service level constraint[J]. IIE Transactions 2003. 35 1049–1055.
[7]Gans, N. A call-routing problem with service-level constraints[J]. Operations Research 2003.51(2) 255–271.
[8]Atlason, J. Call center staffing with simulation and cutting plane methods[J]. Annals of Operations Research.2004. 127(1– 4) 333–358.
[9]Thomas R. Robbins . A stochastic programming model for scheduling call centers with global Service Level Agreements[J]. European Journal of Operational Research. 2010.207(3).1608-1619
[10]Cezik, T. Staffing multiskill call centers via linear programming and simulation[J]. Management Science,forthcoming. 2006.1
[11]Saltzman, R. A hybrid approach to minimizing the cost of staffing a call center[J]. International Journal of Operations and Quantitative Management 2005. 11(1) 1–14.
- 微型电脑应用的其它文章
- 交通信号灯智能控制算法研究
- 基于指纹识别技术的智能门禁系统研究

