莫浅眼前题 『错』题需斟酌

☉江苏省南京市浦口区浦厂中学 谭 宇

背景：

学校模拟网上阅卷，在阅卷过程中收获颇多，学生们的解题方法和思维方式五花八门，不管是正确的还是错误的，远比出卷者预测的要多，有些考生的解题思维远比我们教师想象的要好，他们大胆的猜想和论证给了我不少震动和启发.我被分到第七组，批改第27题（共7人），当时碰到一份考生的试卷解法比较奇特，个人认为是正确的，但有3人否定、2人疑惑、一人不语.于是查找资料，思索探讨，从而就有了下面的论证过程.

过程：

后经研究发现，本题是2008年南京市数学中考试卷第27题第二问，下面是一个学生的解题过程的一小部分：

解：如图1，过点O作OC⊥AB，垂足为点C.

由题意可得：PA=5t，PB=4t.

图1

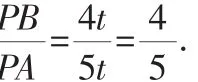
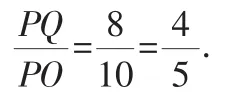
在直角三角形中，可以用边的比来表示两个锐角的三角函数，而从上面的“画线”部分可以看出，该生试图用三角函数推出直角三角形.27题的改卷的部分教师都认为是错误的，毫无道理的，但是我通过大量的实例验证，觉得这个结论是正确的.可以用这样一句话总结：“在三角形中，若一个锐角所对应的余弦值等于这个角两边的比值，那么这个三角形是直角三角形”.下面是证明过程：

求证：△PBA是直角三角形.

图2

又因P′B′=PB，

所以P′A′=PA.

在△P′A′B和△PAB中，

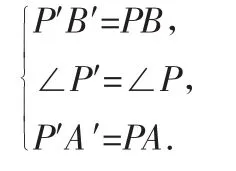
所以△P′A′B≌△PAB（SAS）.

所以∠PBA=∠P′B′A′=90°.

所以△PBA是直角三角形.

有以上结论可见，根据一位学生的“错”解，经过推理论证，从而得到一个新的命题.虽然这位学生没有论证他的猜想，没有得分，但是该为他的大胆猜想而感到骄傲！如果对这个问题的探讨到此为止，那是欠深入的.若能继续探索下去，不仅能提高探索能力而且能体会到做数学的乐趣.

由举一反三的直觉思维，自然想到以下两个推论：

推论1“三角形中，若一个锐角所对应的正弦值等于这个角的对边与它的邻边比值，那么这个三角形是直角三角形”.

推论2“三角形中，若一个锐角所对应的正切值等于这个角的对边与它的邻边比值，那么这个三角形是直角三角形”.

证明：推论1“三角形中，若一个锐角所对应的正弦值等于这个角的对边与它的邻边比值，那么这个三角形是直角三角形”.

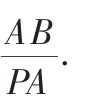
求证：△PBA是直角三角形.

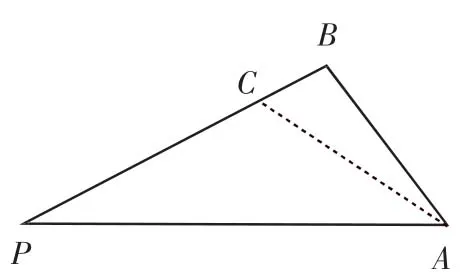
图3

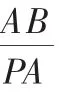
所以AC=AB.

又因AC⊥PB，

根据直线外一点，到直线的所有线段中，垂线段最段且仅有一条，所以点B与点C重合.

即△PBA是直角三角形.

推论2“三角形中，若一个锐角所对应的正切值等于这个角的对边与它的邻边比值，那么这个三角形是直角三角形”.

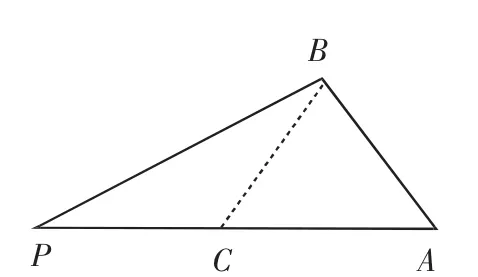
图4

求证：△PBA是直角三角形.

举反例：

倘若△PBA是直角三角形，根据已知条件可得∠PBA=90°，∠A为锐角.过点B，在线段PA上找一点C，使BC=BA.

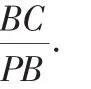
显然△PBC不是直角三角形，所以本题结论不成立.

综上可得，直角三角形的一个新判定：

三角形中，若一个锐角所对应的余弦值等于这个角两边的比值，那么这个三角形是直角三角形.

推论：三角形中，若一个锐角所对应的正弦值等于这个角的对边与它的邻边比值，那么这个三角形是直角三角形.

反思：法国著名雕塑家罗丹说过：“世上并不缺乏美而是缺乏发现美的眼睛”.同样在学习中，教师不可避免会遇到一些学生做的错题，要用辩证的眼光去看待，不要看到不顺眼的或没看过的都一票否决.从探究性学习的观点看，这些错题并不是一无是处，有的蕴含的探索性价值不比“好题”小，因此不应该简单的加以否定.心理学家桑代克认为：“尝试与错误是学习的基本形式.”错误是正确的先导，错误是通向成功的阶梯，学生犯错的过程是一种尝试和创新的过程，教师应该善待学生所犯的错误.英国心理学家贝恩布里说过：“差错人皆有之，而作为教师，对于学生的错误不加以利用是不能原谅的.”但长期以来，对待学生的学习错误，我们更多的是把“错误”当成了教育的“敌人”，以致“不错”便是“成功”，“不错”成了我们不懈的“追求”；在实践中应把其重点放在分析错因、制定对策上.对待学习错误，我们缺乏一种“主动应对”的新理念和策略.有专家指出：“课堂上的错误是教学的巨大财富.”教师应巧妙利用这一“财富”，变解题错误为促进学生发展的资源.