对近几年中考『新定义』型试题的赏析
☉浙江省嵊州市教研室 蔡建锋

随着新课程标准的修订和实施,数学教育要坚持德育为先、全面发展、能力为重、以人为本、与时具进.而“新定义”型数学试题,是以学生已学的数学知识和已有的经验为基础,给出了一个“新概念”,让学生自主阅读和运用这个“新概念”来解决相应的数学问题.这样的试题能较好地体现新课程标准的基本理念,注重培养学生的数学思考、数学阅读理解能力、数学抽象概括能力和对“新概念”的实际应用能力,注重培养学生良好的数学学习习惯.现以绍兴市近六年来的“新定义”型中考题举例说明如下:
例1(2007年)设关于x的一次函数y=a1x+b1与y=a2x+b2,则称函数y=m(a1x+b1)+n(a2x+b2)(其中m+n=1)为此两个函数的生成函数.
(1)当x=1时,求函数y=x+1与y=2x的生成函数的值;
(2)若函数y=a1x+b1与y=a2x+b2的图像的交点为P,判断点P是否在此两个函数的生成函数的图像上,并说明理由.
解:(1)当x=1时,y=m(x+1)+n(2x)=m(1+1)+n(2×1)=2(m+n).
因为m+n=1,所以y=2.
(2)点P在两个函数的生成函数的图像上,设点P的坐标为(a,b).
因为a1×a+b1=b,a2×a+b2=b,所以当x=a时,
y=m(a1x+b1)+n(a2x+b2)=m(a1×a+b1)+n(a2×a+b2)=mb+nb=b(m+n)=b.
即点P在此两个函数的生成函数的图像上.
评注:本试题在学生已学一次函数知识的基础上,通过对两个一次函数解析式的重新组合后,给出了“生成函数”这一新概念,学生通过“新概念”的学习,并运用这一“新概念”来解决相应的问题.第(2)小题有一定的难度,较好地渗透了点的坐标与函数解析式之间的对应关系,许多考生是先求出直线y=a1x+b1与y=a2x+b2的交点坐标,再代入生成函数中加以验证,这样的解法难而繁,无论从知识上还是能力上都超出了新课程标准的要求,导致考生无法得到最后结果.
例2(2008年)定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[2,k-2]的一次函数为正比例函数,求k的值;
(2)设点A,B分别为抛物线y=(x+m)(x-2)与x,y轴的交点,其中m>0,且△OAB的面积为4,O为原点,求图像过A,B两点的一次函数的特征数.
解:(1)因特征数为[2,k-2]的一次函数为y=2x+k-2,
而此函数为正比例函数,所以k-2=0,解得k=2.
(2)由题意知抛物线与x轴的交点为A1(-m,0),A2(2,0),与y轴的交点为B(0,-2m).
因当m=2时,满足题设条件.
故此时抛物线为y=(x+2)(x-2).
它与x轴的交点为(-2,0),(2,0),与y轴的交点为(0,-4).
所以一次函数为y=-2x-4或y=2x-4,
故特征数为[-2,-4]或[2,-4].
评注:本题是以一次函数的解析式中的两个待定系数为知识基础,把能确定一次函数解析式的两个待定系数定义为这个一次函数解析式的“特征数”,揭示了一次函数解析式的本质特征,要求学生理解新定义“特征数”的正确意义和正比例函数与一次函数之间的关系,并运用新概念解决新问题,需要学生具有较好的分析问题和解决问题的能力.
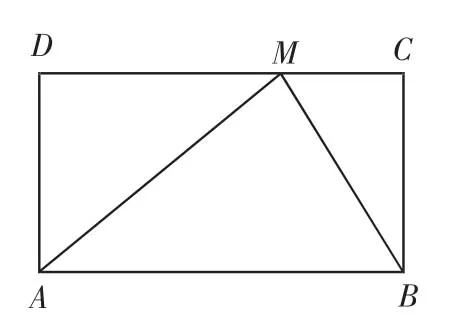
图1
例3(2009年)若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图1所示的矩形ABCD中,点M在CD边上,连AM,BM,∠AMB=90°,则点M为直角点.
(1)若矩形ABCD一边CD上的直角点M为中点,问该矩形的邻边具有何种数量关系?并说明理由;
(2)若点M,N分别为矩形ABCD边CD,AB上的直角点,且AB=4,BC=,求MN的长.
解:(1)因直角点M为CD边的中点,所以MD=MC.
又AD=BC,∠D=∠C=90°,
所以△ADM≌△BCM,∠AMD=∠BMC.
因∠AMB=90°,所以∠AMD+∠BMC=90°.
所以∠AMD=∠BMC=45°,所以AD=DM,所以AB=2AD.
(2)如图2,作MH⊥AB于点H,连接MN.
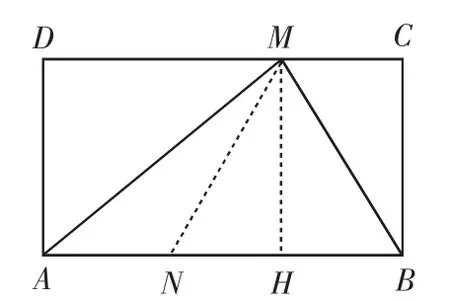
图2
因∠AMB=90°,所以∠AMD+∠BMC=90°.
因∠AMD+∠DAM=90°,所以∠DAM=∠BMC.
又∠D=∠C,所以△ADM∽△MCB.
当MC=1时,AN=1,NH=2.
所以MN2=MH2+NH2=()2+22=7,解得MN=
当MC=3时,MN=BC=.综上所述,MN=或.
评注:本题是在学生已学直角三角形、矩形、和相似三角形等有关知识的基础上,给出了一个矩形的“直角点”的新概念.解决本题的关键是正确理解新概念“直角点”的含义,结合直角三角形全等、相似、勾股定理和矩形的有关性质来解决问题,关注了学生的阅读理解能力和应用已学知识的能力,渗透了分类讨论的数学思想.
例4(2010年)在平面直角坐标系中,一次函数的图像与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图3中的一次函数的图像与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
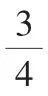
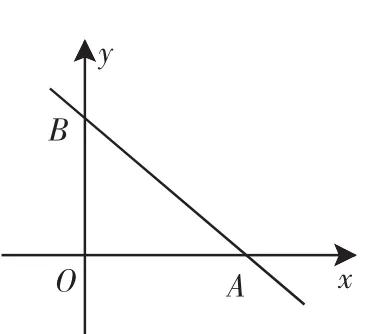
图3
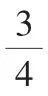
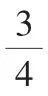
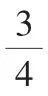
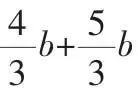
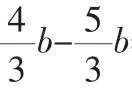
评注:本题是以一次函数的图像与坐标轴为知识背景,把直线与坐标轴围成的三角形定义为此函数的“坐标三角形”,较好地渗透数形结合的数学思想.要求学生理解新定义“此函数的坐标三角形”的正确意义,确定“坐标三角形”的关键是先要确定一次函数的解析式,所以解决(2)首先要对b进行分类讨论来确定函数的解析式,再用新概念来解决问题.
例5(2011年)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.
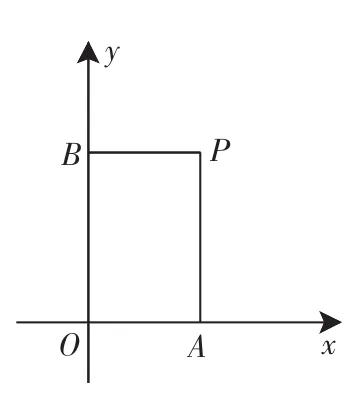
图4
例如,图4中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
解:(1)因1×2≠2×(1+2),4×4=2×(4+4),
所以点M不是和谐点,点N是和谐点.
(2)由题意得:
当a>0时,(a+3)×2=3a,所以a=6.
点P(a,3)在直线y=-x+b上,代入得b=9;
当a<0时,(-a+3)×2=-3a,所以a=-6.
点P(a,3)在直线y=-x+b上,代入得b=-3.
所以a=6,b=9或a=-6,b=-3.
评注:本题是以直角坐标系中点的几何意义和矩形的周长、面积为知识基础,对满足条件的特殊点定义为“和谐点”.要求学生理解新定义“和谐点”的正确意义和点的坐标的几何意义,结合一次函数的解析式,运用图像上的点与函数解析式之间的对应关系,并运用新概念解决新问题,需要学生具有较好的分析问题和解决问题的能力.
例6(2012年)联想三角形外心的概念,我们可引入如下概念.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图5,若PA=PB,则点P为△ABC的准外心.
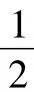
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
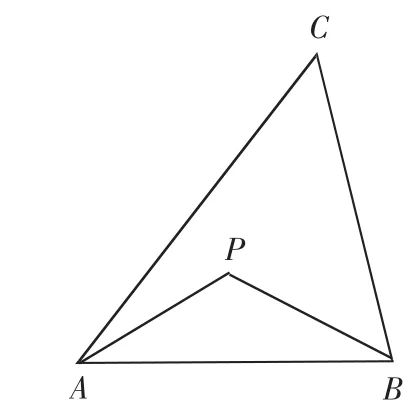
图5
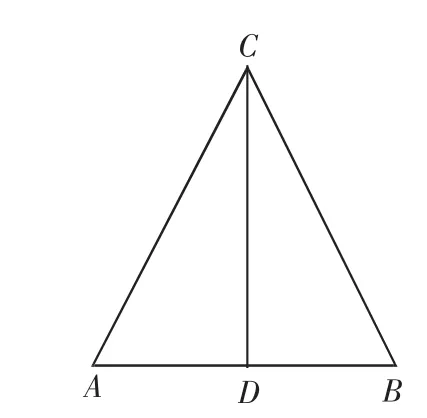
图6
解:应用:①若PB=PC,连接PB,则∠PCB=∠PBC.
因CD为等边三角形的高,所以AD=BD,∠PCB=30°,所以∠PBD=∠PBC=30°.
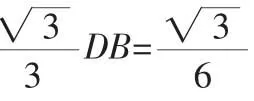
②若PA=PC,连接PA,同理可得PA≠PC.
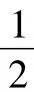
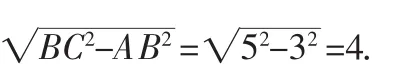
②若PA=PC,则PA=2.
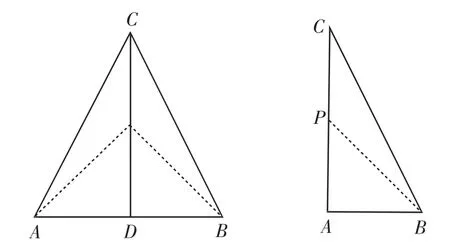
图7
评注:本题是在学生已学三角形外心概念的基础上,给出了三角形“准外心”的定义,通过阅读和理解“到三角形的两个顶点距离相等的点,叫做此三角形的准外心”的定义,让学生经历举例、应用和探究三个不同层次的问题,从简单的阅读理解到特殊性问题,最后要求学生开放性地分类探究,这道题不同于常规几何题,要求学生具有阅读理解、思考分析、类比猜想和分类讨论的能力,这样的试题有利于学生理性思维能力和创新精神的培养.
新定义的试题中所给出的情景是考生所不熟知的,具有背景的新颖而公平的特点.这类问题在设置上充分体现了层次性和基础性,考虑不同层次学生的需求,并为优秀生提供更大的发挥空间.解答“新定义”试题,考生需要通过阅读题目,明白题意,运用知识的类比和迁移,才能解决问题.这类试题较好地考查了学生的知识基础,考查了学生的能力,考查了学生数学直觉、合情推理能力和类比思想,以及数学能力和数学素养.这类问题具有探究价值,对应用新知识解决问题的能力提出了较高的要求,具有良好的效度和区分度.
——《认识直角》教学片断与解读

