普通最小二乘法的几何分析

刘 明

（兰州商学院a.甘肃经济发展数量分析研究中心；b.统计学院，兰州 730020）

普通最小二乘法是线性回归模型最基本最重要的参数估计方法之一。最小，即残差平方和达到最小；二乘，即残差的二次方。它通过构造目标函数——残差平方和，该函数以模型参数估计量为变量，以函数值达到最小来确定参数估计量的取值。普通最小二乘法在数学上构造计技巧性强，且便于理解和操作，在满足高斯假定情况下普通最小二乘估计量又具有良好的性质，因此为人们所推崇。普通最小二乘法简单易行，但很多人对其可以灵活掌握却不能达到充分理解，例如，为什么“残差向量与解释变量正交”和“残差平方和最小”两种情形是等价的？究其原因，是这种方法在本质上是一种数学方法，需要从数学的角度进行分析和进一步的认识。本文从普通最小二乘估计的方法出发，在矩阵分析的基础上，提出了一种几何方法求解普通最小二乘估计量，从几何的角度考察分析普通最小二乘法。

1 普通最小二乘法的矩阵分析

普通最小二乘法的实现过程较为简单，首先是构造残差平方和函数，再利用微分学中求极值的办法构造残差平方和达到最小的条件，即分别对参数估计量求偏导函数，并令其等于零，由此得出关于参数估计量的线性方程组，解线性方程组即可得出普通最小二乘估计量。如果设线性回归模型的残差为ei，普通最小二乘法就是使得达到最小以确定参数估计量。作为参数估计中最基本的方法之一，这里无须详述。下面以矩阵为工具分析研究线性回归模型的普通最小二乘估计量。

考虑矩阵形式的样本回归模型：

模型的普通最小二乘估计量用矩阵表示为：

残差向量e可以表示为：

拟合值可以表示为：

由于:

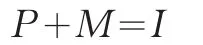
因此:

即普通最小二乘法将Y分解成了和e两者之和的形式。

再分析和e的关系，容易验证两者是正交的，即:

因此，普通最小二乘法将Y分解成了相互正交的两部分之和:

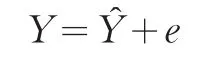
2 普通最小二乘法的几何原理

为进一步对普通最小二乘估计量做出分析，首先给出一个定理。

定理：设X为任一矩阵，则向由X生成的子空间的投影矩阵为

该定理的证明参见参考文献[2]。

根据式（1），由上述定理可知是Y在X上的投影。为说明这个问题，令研究的对象是一个二元模型:

如果样本容量为n，则y,x1,x2则各自形成了n维向量。因此可设y,x1,x2三个向量来自n维欧氏空间，则x1,x2生成n维欧氏空间的一个子空间，做出相应的空间图。

图 y向量的分解

设向量y,x1,x2均以O为始点。向量x1,x2所生成的空间直接来看就是一平面，根据前述定理，向量̂即为向量y在x1,x2平面上的投影，显然在x1,x2平面上。如图所示，设向量y的终点为C，向量的终点为T，根据向量加法运算不难发现:

因此向量TC即为残差向量e。

根据投影的定义可知，向量e和投影空间是正交的，而向量1、x2在投影平面内，因此e和它们均为正交关系，即:

此结论对应于线性回归模型中的下述结论：

将y向量完成上述分解后，下面考察分析几何法求解普通最小二乘估计量的实现路径。

过T点分别作向量x2、x1的方向平行线，交x1、x2于A、B点，根据向量运算的平行四边形法则可知:

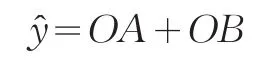
其中OA、OB均为向量。OA、OB分别和向量x1、x2同向，因此有:

根据样本回归直线:

再结合向量分解的唯一性可知:

其中截距项通过坐标平移即可得到，不影响此处的分析结论。可通过对残差向量各分量取均值即可得到，将模型加上截距项，其本质是将残差向量进行了平移。

由投影的唯一性可知，与x1、x2平面正交的残差向量是唯一的，因此，普通最小二乘法对对y进行了关于x1、x2唯一的正交分解。其它任意分解（包括正交和非正交）所得残差向量必然与x1、x2线性相关。此结论可以推广至任意元线性回归模型。

现在分析几何法普通最小二乘估计量的实现过程。y,x1,x2均为已知向量，因此y向量与x1、x2平面的夹角是可测的，根据y与x1、x2平面的夹角即可计算出投影向量。向量OA、OB的方向分别与x1、x2通向，即OA、OB方向已知，根据向量分解的唯一性，即可计算出分解出的两个向量OA、OB。因此，向量OA、OB的模长是可求得的，而x1、x2的模长是已知的，于是普通最小二乘估计量可通过（2）求得。

当向量x1与x2正交时，即x1⊥x2，连接C、A两点和C、B两点，不难证明：

CA⊥x1，CB⊥x2

因此可知向量OA是向量y在x1上的投影，向量OB是向量y在x2上的投影。于是有：

此处未考虑截距项，即不考虑坐标平移。因此有如下结论：

当解释变量相互正交时，被解释变量对所有解释变量进行回归所得到的偏回归系数估计量分别与对单个解释变量回归时的系数估计量对应相等。

以上以二元回归模型为例论述了普通最小二乘估计量的几何求解方法，对于多元线性回归模型同样可以使用几何法求解普通最小二乘估计量。不妨设多元线性回归模型中有k个解释变量，则由此k个解释变量可生成一个子空间，̂即为向量y在该子空间内的投影，在子空间内，可由空间内的向量线性表出；残差向量e=y-与该子空间内的任意向量正交。根据向量的分解即可得到在每个解释变量上的分量，进而求得普通最小二乘估计量。计算原理和上述二元回归模型是一致的，但计算过程更为复杂，由于是多维空间，因此不便于用坐标图进行解释分析。

3 结论

由上述分析过程可以看出，普通最小二乘法的数学本质是将研究对象即被解释变量分解为相互正交的两部分，即线性回归模型中的确定部分和随机部分，确定部分是解释变量的线性组合，由解释变量线性表出，而随机部分则与解释变量线性无关。通过欧氏空间向量理论和几何作图的方式可以描述普通最小二乘法下的变量的分解过程，使得普通最小二乘法的实现过程更为直观。在此基础上可以依据空间向量理论和几何分析方法进一步求得由向量表示的普通最小二乘估计量。

[1]威廉·H·格林.计量经济分析[M].北京：中国人民大学出版社，2007.

[2]陈希孺，陈桂景，吴启光，赵林城.线性模型参数的估计理论[M].北京:科学出版社，1985.