非负约束全变差正则化方法在动态光散射颗粒粒度分布反演中的应用

王田田，申 晋，刘 伟，孙贤明

（山东理工大学电气与电子工程学院，山东淄博255091）

20世纪60年代以来，动态光散射（Dynamic Light Scattering，DLS）技术已成为亚微米、纳米级颗粒粒径测量的主要手段［1]．动态光散射技术的测量原理建立在颗粒的布朗运动基础上，在分散介质中，颗粒的运动使得散射光强随时间不断地起伏涨落，这种涨落与颗粒的粒径有关，粒径越小，涨落越快．测量颗粒散射光信号的相关函数，再由相关函数反演出颗粒的粒径分布，因此，动态光散射也称为光子相关光谱（Photo Correlation Spectroscopy，PCS）技术．由相关函数反演颗粒粒度分布需求解第一类Fredholm积分方程，其高度病态性决定了原始数据微小的扰动都可能导致所求解与真实解的巨大偏离［2]．为解决这个问题，人们提出和应用了多种颗粒粒度反演算法，包括累积分析法、拉普拉斯变换法、指数采样法、CONTIN算法、非负最小二乘法、Tikhonov正则化方法及截断奇异值分解法［3－9]，但每种方法都有其适用范围和局限性．一些改进的算法和颗粒粒度反演新方法不断地被提出，包括改进的累计分析法［10]、非负最小二乘截断奇异值分解法［11]、改进的正则化方法［12]及遗传算法［13]、神经网络算法［14]等智能优化算法．其中正则化方法因其较简单的理论框架而得到广泛的应用．

本文采用全变差（Total Variation，TV）正则化方法将离散的积分方程化为非线性最优化问题，并用固定点迭代法（Lagged Diffusivity Fixed Point Method）求解．实际测量中，粒度分布的误差水平是不可知的，而反演过程中所用的系数矩阵A＇A是正定矩阵，固定点迭代法全局收敛［15]，所以算法的终止不取决于分布的误差水平．非负约束条件的引入有效地消除了分布中无意义的负值．

1 动态光散射技术与全变差正则化反演

对随机的散射光信号进行时间自相关运算并作归一化处理，可以得到归一化的散射光强自相关函数g（2）（τ），它与归一化的电场自相关函数g（1）（τ）的关系为

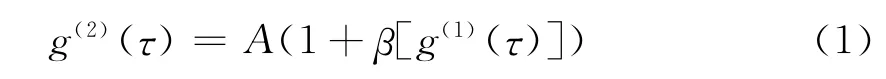
式中，τ是延迟时间，A是实验基线，β是相干因子．对于多分散颗粒系，归一化的电场自相关函数

式中∫∞0G（Γ）dΓ＝1，是归一化的衰减线宽分布函数Γ为衰减线宽DT为平移扩散系数；q为散射矢量；kB是波尔兹曼常数；T代表绝对温度；η为溶液粘度系数；d为颗粒直径；n为溶液的折射率；λ0为激光在真空中的波长；θ为散射角．

式（2）为第一类Fredholm积分方程，从带有噪声的g（1）求解颗粒粒径属于病态问题（ill－posed problem）．原始数据的微小扰动将导致解的严重偏离．求解时，将式（2）离散化为

采用全变差正则化方法求解式（3）．全变差正则化方法采用非线性正则化算子，实质是基于全变差惩罚的最小二乘方法［16]，即指求解如下最优化问题

式中α为正则化参数；TV（x）为正则化算子，起着恢复解的稳定性的作用．

由式（4）所得的结果中往往出现负解，因此对式（4）进行非负约束，即非负TV正则化

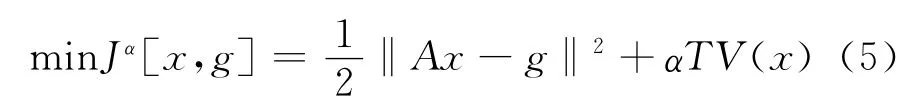
TV（x）为函数x定义在区间I＝［0，1] 上的全变差函数

要求得式（5）的极小值，首先要求Jα［x，g] 的梯度，由于TV（x）关于x是不可微的，TV（x）的梯度很难获得，因此用一个光滑的泛函逼近TV（x），最优化问题化为

式中β0为正的常数．

采用固定点迭代法求解非线性最优化问题（7），求解步骤如下：

（1）设定迭代次数k＝50，假定初始粒度分布z＝0．

（2）计算L（通过离散全变差方程计算得到）．

（3）求解Jα［x，g] 的梯度，grad［Jα［x，g] ] ＝A＇（Ax－g）＋αLx．

（4）求解Jα［x，g] 的Hessian矩阵，Hessian［Jα［x，g] ] ＝A＇A＋αL．

（5）计算Sk＋1＝－Hessian［Jα［x，g] ]－1grad［Jα［x，g] ]k．

（6）更新分布xk＋1＝xk＋Sk＋1，直到满足设定的迭代次数．

本文采用L曲线准则［17]选择正则化参数α，即以log－log尺度描述‖xk‖与‖Axk－g‖的曲线，该曲线呈明显的L状，曲线拐角处的值即取为正则化参数．

2 数值模拟

利用非负约束TV正则化，对动态光散射反演问题进行数值模拟．计算过程中采用Johnson’s SB分布函数作为模拟的真实粒径分布［18]，该函数的表达式为

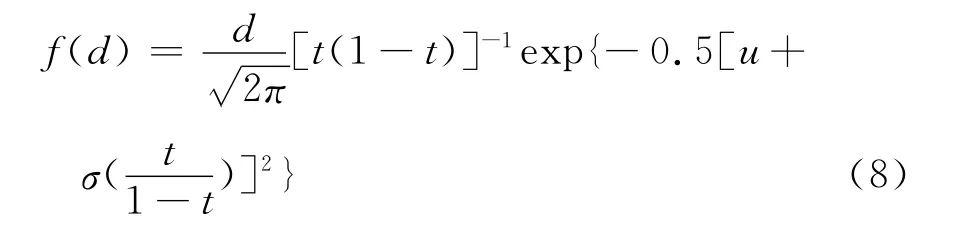
式中，t＝（d－dmin）／（dmax－dmin）为归一化尺寸，dmax和dmin是粒子的最大和最小的粒径；u和σ是分布参数，通过改变这两个参数，能模拟出不同的分布形式．

模拟实验条件为入射光在真空中的波长λ0＝632．8nm，溶液的折射率n＝1．331，绝对温度T＝298K，波尔兹曼常数kB＝1．3087×10－23J·K－1，溶液粘度系数η＝0．89×10－3Pa·s，散射角θ＝90°．

反演结果中，用分布误差和峰值误差来衡量反演得到的颗粒粒度分布（Particle Size Distribution，PSD）与真实粒度分布的匹配程度．分布误差越小，峰值误差越小，反演得到的分布越接近真实的粒度分布．本文给出的所有粒度分布均为五次反演结果的平均值．

2．1 无噪声时单峰和双峰颗粒粒度分布反演

单峰分布情况下，模拟初始粒径分布参数为u＝0．8，σ＝1．5，αmax＝600nm，αmin＝100nm；双峰分布颗粒为两个等份额的单峰Johnson’s SB函数之和，参数为u1＝－3．2，σ1＝2．8，u2＝3．4，σ2＝2．1，αmax＝900nm，αmin＝100nm．单峰分布、双峰分布颗粒的粒径反演范围初始值分别取［0，700] ，［0，1 000] ．单峰分布和双峰分布的无噪声相关函数反演结果分别如图1、图2所示．

图1 无噪声单峰分布反演

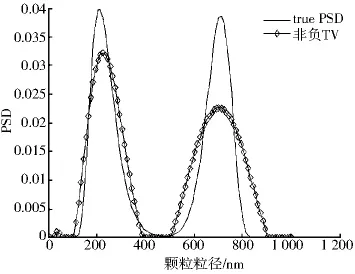
图2 无噪声双峰分布反演

由图1和图2可以看出，非负TV正则化方法能很好地反演出单峰分布和双峰分布，其中，单峰分布的分布误差为0．013 3，峰值误差为0；双峰分布的分布误差为0．061 5，第一个峰的峰值误差为4．65%，第二个峰的峰值误差为1．39%．在无噪声情况下，非负TV正则化反演颗粒粒度分布是可行的．

2．2 加入噪声时单峰和双峰颗粒粒度分布反演

为了验证算法的抗噪声能力，分别在上述两种颗粒的无噪声模拟相关函数中加入噪声水平为0．01的噪声，其中噪声相关函数为

g＿noise＝g＋noise＿level＊rand（N，1）；式中noise＿level为噪声水平．

粒径反演范围初值同上．由非负TV正则化反演得到的单峰分布和双峰分布如图3和图4所示．

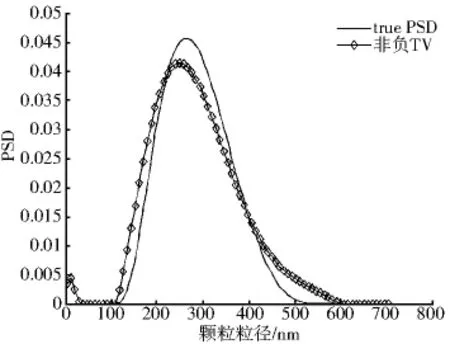
图3 噪声水平为0．01时单峰分布反演结果

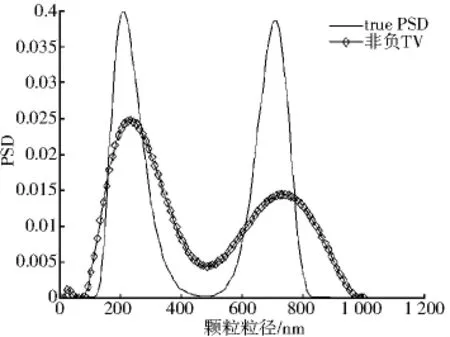
图4 噪声水平为0．01时双峰分布反演结果

由图3和图4看出，加入噪声水平为0．01的噪声后，反演出的分布较大的偏离真实分布．单峰分布的分布误差为0．0344 9，峰值误差为6．56%；双峰分布的分布误差为0．089 9，第一个峰的峰值误差为9．31%，第二个峰的峰值误差为2．8%．虽然加入噪声后，分布误差和峰值误差加大，但均在可接受范围内．所以非负TV正则化具有一定的抗噪声能力．

3 实验结果

实验温度为25℃．光电倍增管在90接收散射光信号．实验样品为粒径150nm（3150A）、60nm（3060A）和200nm（3200A）的聚苯乙烯乳胶颗粒．分散介质（水）的折射率为1．331．采用非负TV正则化方法反演测得的两种颗粒系的相关函数，结果如图5、图6所示．

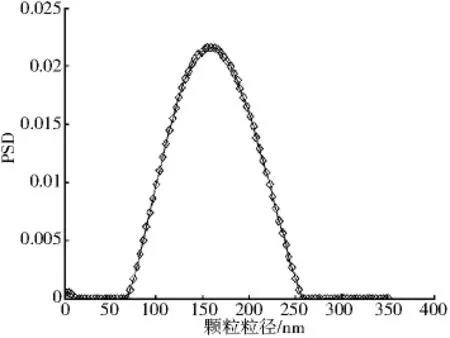
图5 150nm聚苯乙烯颗粒反演结果

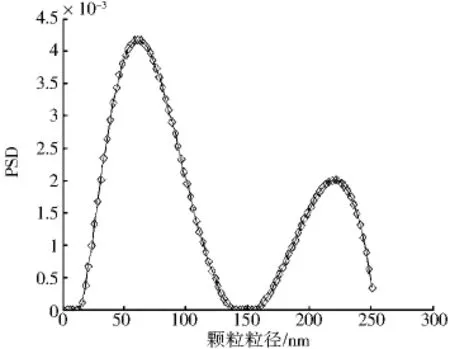
图6 60nm和200nm混合颗粒反演结果

由非负TV正则化反演的150nm聚苯乙烯乳胶颗粒系的峰值为159．3nm，误差为6．20%；反演的60nm和200nm混合颗粒的第一个峰值为61．3 nm，第二个峰值为221nm，第一个峰的峰值误差为2%，第二个峰的峰值误差为10．7%．非负TV正则化可以反演出实际的单分散和双分散颗粒系．

4 结束语

本文采用全变差正则化方法对模拟和实验数据进行了分析．结果表明，在无噪声情况下，TV正则化反演的单峰分布和双峰分布的分布误差小于0．0615，峰值误差小于4．65%．在相关函数中加入噪声水平为0．01的噪声后，分布误差小于0．089 9，峰值误差小于9．31%，所以，全变差正则化能较好地反演出单峰分布和双峰分布．通过反演150nm标准颗粒和由60nm与200nm组成的混合颗粒验证了这一结论．

［1] Pecora R．Dynamic light scattering：application of photon correlation spectroscopy［M] ．New York：Plenum Press，1985．

［2] 肖庭延，于慎根，王彦飞．反问题的数值解法［M] ．北京：科学出版社，2003：8－17．

［3] Koppel D E．Analysis of macromolecular polydispersity in intensity correlation spectroscopy：the method of cumulants［J] ．The Journal of Chemical Physics，1972，57：4 814－4 820．

［4] McWhirter J G and Pike E R．On the numerical inversion of the Laplace transform and similar Fredholm integral equations of the first kind［J] ．Phys．A Math．Theor，1978，11：1 729－1 745．

［5] Ostrowsky N，Sornette D，Pike E R．Exponential sampling method for light－scattering polydispersity analysis［J] ．Mod Opt，1981，28：1 059－1 070．

［6] Provencher S W．A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations［J] ．Computer Physics Communication，1982，27：229－242．

［7] Iqbal M．On photon correlation measurements of colloidal size distributions using bayesian strategies［J] ．J Comput Appl Math，2000，126：77－89．

［8] 李功胜，于杰．一种新的求解第一类Fredholm积分方程正则化的数值分析［J] ．山东理工大学学报：自然科学版，2003，17（2）：5－8．

［9] Ubera J V，Aguilar J F，Gale D M．Reconstruction of particlesize distribution from light－scattering patterns using three inversion methods［J] ．Appl Opt，2007，40：124－132．

［10] Frisken B J．Revisiting the method of cumulants for analysis of dynamic light－scattering data［J] ．Appl．Opt，2001，40：4 087－4 091．

［11] Zhu X J，Shen J．Nonnegative least－square truncated singular value decomposition to particle size distribution inversion from dynamic light scattering data［J] ．Appl Opt，2010，49（34）：6 591－6 596．

［12] Arias M L，Frontini G L．Particle size distribution retrieval from elastic light scattering measurement by a modified regularization method［J] ．Part．Part．Syst．Charact，2006 23：374－380．

［13] Ye M，Wang S．Inversion of particle－size distribution from angular light－scattering data with genetic algorithms［J] ．Appl Opt，1999，38（12）：2 677－2 685．

［14] Gugliotta L M，Stegmayer G S．A neural network model for estimating the particle size distribution of dilute latex from multiangle dynamic light scattering measurements［J] ．Part Part Syst Charact，2009 26：41－52．

［15] Vogel C R．Computational methods for inverse problems［M] ．Siam，Frontiers in Applied Mathematics，2002，130－136．

［16] 王彦飞．反演问题的计算方法及其应用［M] ．北京：高等教育出版社，2007，38－49．

［17] Agarwal V．Total variation regularization and L－curve method for the selection of regularization parameter［D] ．2003，4－7．

［18] 李绍新．动态光散射测量粒径分布的格雷码编码遗传算法反演运算［J] ．计算物理，2008，25（3）：323－329．