多粒度空间中的粗糙隶属度与知识粒度

杨习贝，颜 成，陈 才，於东军

(1.江苏科技大学 计算机科学与工程学院，江苏镇江 212003;2.南京理工大学计算机科学与技术学院，南京 210094;3.江苏尚博信息科技有限公司，江苏无锡 214072)

0 引言

作为粒计算的一种重要数学模型，粗糙集理论在模式识别、知识发现、决策分析、医疗诊断等众多领域已经取得了很大的进展。

传统粗糙集及其很多拓展模型是建立在一个二元关系基础上的，这个二元关系可以是不可分辨关系、相容关系、序关系甚至是没有任何约束条件的二元关系。根据某个特定二元关系，可以得到论域上的一个划分或者覆盖，这个划分或者覆盖实际上是一些信息粒的合集，因而可将这个合集视作一个粒空间。从这个角度来看，这些粗糙集方法是在一个粒空间中进行概念的近似逼近，因而是单粒度空间中的粗糙集。

然而，随着研究的不断深入以及应用需求的不断增加，单粒度粗糙集方法在很多数据处理问题上不再适用。例如，在决策分析问题中，多个决策者之间的关系有可能是相互独立的，因而需要在多个相互独立的粒空间中进行目标的近似逼近。从这个观点出发，钱宇华、梁吉业等人提出了多粒度粗糙集的概念。多粒度粗糙集与单粒度粗糙集最本质的区别是可以使用一族而非单个粒空间中的知识来进行概念的近似逼近。

在文献［5］中，钱宇华、梁吉业等人将由一族等价关系所形成的论域上的一族划分看作一个多粒度空间，在这个空间中，给出了乐观多粒度粗糙集模型。与此同时，他们将这种乐观多粒度粗糙集模型引入不完备信息系统，采用一族容差关系构建多粒度空间。在此基础上，他们又在由一族划分所构成的多粒度空间中，给出了悲观多粒度粗糙集模型。在上述这些工作中，多粒度空间是由一次性给出的一族二元关系得到的，因而可将其视作同步多粒度方法。

为了降低粗糙集理论中知识约简及规则抽取的算法复杂度，钱宇华、梁吉业等人提出了基于正向近似的通用特征选择加速算法。这种算法以核属性集为起点，根据正向近似方法逐次从论域中去掉协调部分的对象。正向近似采用一个使得多粒度空间逐渐细化的偏序关系来表述目标概念，这种方法可被视作异步多粒度方法。

1 多粒度粗糙集模型

令U为一个非空有限论域，R={R1，R2，…，Rm}为论域上一族等价关系的集合，称二元组(U，R)为一个知识基。

定义1 令(U，R)为一知识基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，对于∀X⊆U，X的乐观多粒度下近似集合(X)与上近似集合(X)分别定义为:

定义2 令(U，R)为一知识基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，对于∀X⊆U，X的乐观多粒度下近似集合RP(X)与上近似集合RP(X)分别定义为:

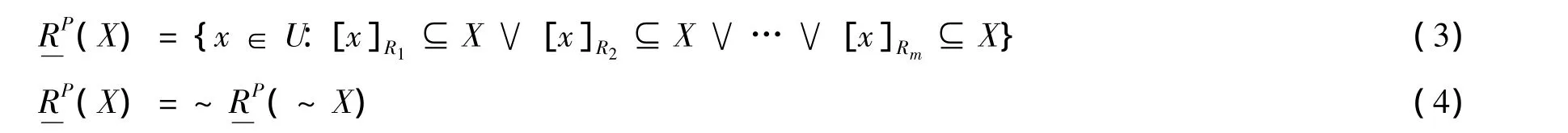
由定义1和定义2可以看出，乐观多粒度下近似要求至少有一个粒度层次上的等价类包含在目标概念中，而悲观多粒度下近似则要求所有粒度层次上的等价类都包含在目标概念中，因而悲观多粒度下近似的要求比乐观多粒度下近似的要求更严格。乐观多粒度上近似和悲观多粒度上近似都是根据其下近似的补集来定义的。据此，很容易得到如下性质。

定理1 令(U，R)为一知识基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，对于∀X⊆U，有:

定义3 令(U，R)为一知识基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，则多粒度粗糙隶属度函数有如下两种形式的定义:

很明显，多粒度空间下的粗糙隶属度依然满足性质0≤maxμRX(x)≤1，0≤minμRX(x)≤1。

定理2 令(U，R)为一知识基，其中 R1，R2…Rm∈ R，令 R={R1，R…Rm}，有

证明:仅证式(9)，其他证明过程类似。

定理3 令(U，R)为一知识基，其中R1，R2…，Rm∈R，R={R1，R2…Rm}，若R1⊆R2⊆…⊆Rm，则对于∀X⊆U，有:

定理3 在一个多粒度空间中，随着等价关系的嵌套变化，乐观多粒度下、上近似集与最粗粒度等价关系所得到的下、上近似是等价的;悲观多粒度下、上近似集与最细粒度等价关系所得到的下、上近似是等价的。

2 多粒度空间中的知识粒度

2.1 知识粒度的两种定义方式

令(U，R)为一知识基，其中R1，R2…Rn⊆R，则每个等价关系族Ri(1≤i≤n)所构成的划分就组成了一个多粒度空间。形如:

需要注意的是，多粒度空间MSi不是论域上一族子集的合集，而是由m个划分所构成的合集，所有的等价关系族R1，R2…Rm所构成的划分就组成了n个多粒度空间。形如:

定义4 令(U，R)为一知识基，其中R1，R2…Rm∈R，令R={R1，R2…Rm}，则多粒度空间中的知识粒度有如下两种形式的定义:

由于本文是基于划分的多粒度空间进行讨论的，所以定义4中的知识粒度有如下等价的形式:

类似于经典粗糙集理论，多粒度空间中的知识粒度也表示了一族等价关系的分辨能力。若知识粒度越大，则表示多粒度空间的分辨能力越弱;若知识粒度越小，则表示多粒度空间的分辨能力越强。当等价关系族R中只有一个等价关系时，多粒度空间中的知识粒度GK∩(R)和GK∪(R)就退化为经典粗糙集理论中知识粒度的定义。根据上述讨论，显然有:

(1)若∃Ri∈R使得U/Ri={x:x∈U}，则知识粒度GK∩(R)达到最小值;

(2)若∀Ri∈R使得U/Ri={x:x∈U}，则知识粒度GK∪(R)达到最大值;

(3)若∀Ri∈R使得U/Ri={U}，则知识粒度GK∩(R)达到最大值 1;(4)若∃Ri∈R使得U/Ri={U}，则知识粒度GK∪(R)达到最大值1。

2.2 基于知识粒度的多粒度空间约简

根据定义4中所示的两种知识粒度的定义，下面讨论如何对多粒度空间进行约简。多粒度空间的约简就是在多粒度空间中根据一定的约束条件，删除一些冗余的粒空间。由于在多粒度空间中，知识粒度有“交”和“并”两种形式，所以可以分别将这两种知识粒度作为启发式函数来对多粒度空间进行约简。

定义5 令(U，R)为一知识基，其中 R1，R2…Rm∈ R，令 R={R1，R2…Rm}，∀R＇⊆ R。

(1)若GK∩(R＇)=GK∩(R)，则称R＇是R的一个“交”协调集;

(2)若 R＇是R的一个“交”协调集且对于∀R＇＇⊆R＇，R＇＇都不是R的“交”协调集，则称R＇是R的一个“交”约简;

(3)若GK∪(R＇)=GK∪(R)，则称R＇是R的一个“并”协调集;

(4)若 R＇是R的一个“交”协调集且对于∀R＇＇⊆R＇，R＇＇都不是R的“并”协调集，则称R＇是R的一个“并”约简。

根据定义5可知，R的“交”约简是保持多粒度空间中知识粒度GK∩(R)不变的最小等价关系子集;而R的“并”约简则是保持多粒度空间中知识粒度GK∪(R)不变的最小等价关系子集。这两种约简的概念都可以在等价关系族R中约去一些冗余的等价关系，从而简化由等价关系族R所形成的多粒度空间。

类似于粗糙集理论中的启发式约简算法，以下给出定义5中约简算法的一般步骤。

2.2.1 求多粒度R的一个“交”约简

输入:等价关系族R={R1，R2…Rm}，输出:R的一个“交”约简R＇。步骤如下:

第1步，令R＇= Ø;

第2步，判断GK∩(R＇)=GK∩(R)是否成立，若成立，转第6步，否则转第3步;

第3步，对于 ∀Ri∈ R-R＇，计算 GK∩(Ri∪ R＇);

第4步，取一个等价关系 Rj∈ R-R＇满足 GK∩(Rj∪ R＇)=min{GK∩(Ri):Ri∈ R-R＇};

第5步，令R＇=Rj∪R＇，判断GK∩(R＇)=GK∩(R)是否成立，若成立，转第6步，否则转第3步;

第6步，输出“交”约简R＇。

让我们回到“der Morgenstern ist die Venus”这个句子上来。此处“ist”的确不是传统意义上的系词，而是一个类似于“killed”的关系词，即带有两个空位的概念词，它本身作为质料的一部分构成了对无序的相等关系的表达：“( ) ist ( )”，此时它的前后只能填入专名。

2.2.2 求多粒度R的一个“并”约简

输入:等价关系族R={R1，R2…Rm}，输出:R的一个“并”约简R＇。

步骤如下:

第1步，令R＇= Ø;

第2步，判断GK∪(R＇)=GK∪(R)是否成立，若成立，转第6步，否则转第3步;

第4步，取一个等价关系 Rj∈ R-R＇满足 GK∪(Rj∪ R＇)=min{GK∪(Ri):Ri∈ R-R＇};

第5步，令R＇=Rj∪R＇，判断GK∪(R＇)=GK∪(R)是否成立，若成立，转第6步，否则转第3步;

第6步，输出“并”约简R＇。

上述两种算法的复杂度是O(m2)，其中m表示等价关系族R中等价关系的数目。

3 结论

本文以多粒度空间为研究对象，针对多粒度粗糙集模型和多粒度空间约简问题进行了讨论，提出了两种形式的多粒度粗糙隶属度函数，这两种多粒度粗糙隶属度函数是经典粗糙集理论中粗糙隶属度函数的拓展形式。在多粒度粗糙隶属度函数的基础上，重构了乐观和悲观多粒度粗糙集。以多粒度空间中多个等价关系的交、和、并为基础，定义了多粒度空间中两种知识粒度的度量方式，并以这两种度量为函数，给出了多粒度空间约简的概念及启发式算法。

［1］Z.Pawlak.Rough sets-theoretical aspects of reasoning about data［M］.Netherland:Kluwer Academic Publishers，1991.

［2］Y.H.Qian，J.Y.Liang，Y.Y.Yao，et al.MGRS:a multi-granulation rough set［J］.Information Sciences，2010，180:949-970.

［3］Y.H.Qian，J.Y.Liang，C.Y.Dang.Incomplete multigranulation rough set［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A，2010，20:420-431.

［4］Y.H.Qian，J.Y.Liang，W.Wei.Pessimistic rough decision［J］.Journal of Zhejiang Ocean University:Natural Science，2010，29(5):440-449.

［5］钱宇华.复杂数据的粒化机理与数据建模［D］.太原:山西大学，2011.

［6］Y.H.Qian，J.Y.Liang，W.Pedrycz et al.Positive approximation:An accelerator for attribute reduction in rough set theory［J］.Artificial Intelligence，2010，174(9):597-618.

［7］钱宇华，梁吉业，王锋.面向非完备决策表的正向近似特征选择加速算法［J］.计算机学报，2011，34(3):435-443.