我国工业行业二氧化碳排放绩效—基于Luenberger生产率指数分析
刘金萍
(淮安市淮阴区王营镇财政所,江苏淮安 223300)
0 引言
近年来,二氧化碳排放引起国际社会的高度重视。尽管二氧化碳是大气的重要成分,而且在自然界二氧化碳保证了绿色植物进行光合作用和海洋浮游植物呼吸的需要,但它是引起温室效应的主要成分。因此,减少二氧化碳等温室气体排放是全球共同的责任。1992年,联合国通过了《联合国气候变化框架公约》,《公约》的目标是“将大气中温室气体的浓度稳定在防止气候系统受到危险的人为干扰的水平上”,同时明确规定发达国家与发展中国家之间负有“共同但有区别的责任”。1997年,公约第三次缔约方会议在日本京都举行,并制定了《京都议定书》。《京都议定书》签署目的在于要求发达国家减少和控制温室气体排放至少比1990年水平下降5%。中国作为发展中国家在《京都议定书》框架下尽管没有减排任务,但作为一个负责任的大国提出中国自己减排目标,即争取到2020年实现单位GDP的二氧化碳排放量比2005年水平下降40% ~45%的目标。然而,我国正处于工业化时期,化石能源需求将会不断增加,同时我国又是发展中国家,摆脱贫困,提高收入水平仍是一项历史使命。所以,加快经济发展同时又要达到碳减排行动目标是一对矛盾,而解决这一矛盾的关键是提高能源和原材料的使用效率。
事实上,二氧化碳排放主要由化石能源、原材料消耗和经济活动所决定,其中我国工业能源消耗占总能源消耗80%以上。为了分析在碳排放约束条件下能源和原材料使用效率,我们必须使用新的方法。传统有关生产效率测度仅考虑市场性的合意的产出,没有考虑生产过程中产生的非市场性非合意的产出,例如CO2的排放。这主要是由于研究者无法得到非合意产出的价格信息,传统生产率的测度方法使得生产率增长的测算出现了偏差。为了分析在碳排放约束条件下能源和原材料消耗的生产率的变化,我们采用非参数数据包络分析方法,这种方法仅需要投入、产出和污染排放的数据可以估计方向性距离函数,这个函数主要用来测量全要素生产率的Luenberger生产率指数,这个指数同时考虑了合意产出的提高和非合意产出的减少。它已被广泛地使用在工业部门(Fare et al.2001)、地区(Hailu,et al.2001)和国家(Lindenberg,2004Domazlick and Weber, 2004;Yoruk and Zaim, 2005;Kumar,2009)。
本文的目的是运用我国投入产出表的相关数据评价我国工业环境绩效,并对我国工业行业在碳排放约束条件下和传统的Luenberger生产率指数进行对比,分析Luenberger生产率指数变化的原因。
1 研究方法
传统测量TFP的方法通常忽略非合意的产出,但是Farr.ed al.(2001)认为忽略非合意产出来评估全要素生产率是不准确的。由Caves et al.(1982)提出的 Malmquist生产率指数被 Farr.ed al.(1994)更进一步发展了,他们使用 Shepherd’s距离函数和非参数线性规划方法来测量OCED生产率的变化。Malmquist生产率指数对于我们研究有许多优点,它是一个全要素生产率指数,可以分解成效率变化指数和技术变化指数,既能够反映环境规制条件下静态效率又能够反映动态效率。
但是,值得注意的是合意的产出伴随着非合意的产出。将非合意产出纳入到传统Malmquist生产率指数会产生一些问题。在计算包含非合意产出Malmquist生产率指数时,假如合意产出增加,那么非合意产出也随之增加(Farere和Grosskopf,2000),这时依靠传统距离函数的Malmquist生产率指数便无法计算全要素生产率,计算结果会发生偏差。因此,我们必须使用方向距离函数,这种方法能够分拆成合意产出和非合意产出,并且能够增加合意的产出,同时减少非合意的产出。本文应用以方向距离函数为基础发展而来Luenberger生产率指数,这个方法不仅具有方向距离函数的优点,同时避开Malmquist-Luenberger生产率指数需要投入或者产出径向的缺点。
1.1 生产集
假设每一个产业使用N种投入x=(x1,x2,…,xN)∈得到M种合意产出y=(y1,y2,…,yM)∈,以及I种非合意产出b=(b1,b2,…,bt)∈,用P(x)表示生产可行性集:

我们假设生产可行性集是一个闭集和有界集,合意的产出和投入是自由处置的。我们有三个假设:
假设1:如果(y,b)及0≤θ≤1,则(θy,θb)∈P(x)。
假设1叫做产出弱可处置性假定,即合意产出和非合意产出同比例减少,这个假定意味着,若要减少非合意产出就必须减少合意产出,表明为了减少产业二氧化碳排放,就将一定比例的合意产出。
假设2:如果(y,b)∈P(x)及b=0,则y=0。
假设2叫做零结合假定,这个假定意味着一个国家如果没有非合意产出,就没有合意产出,或者说,有合意产出就一定有非合意产出,这个零结合假定是Shepherd和Fatere(1974)提出。
假设3:如果(y,b)∈ P(x)及 y'≤ y,则(y',b)∈P(x)。
这个假定意味着,合意的产出在没有减少非合意的情况下可以较少,合意的产出和投入是自由处置的和具有强可处置性。
假定合意的产出与非合意是零结合和产出弱可处置,在满足假定条件下,Fare et al(1994)构建如下DEA模型:

模型中t表示时期,K表示地区,z'k表示每一个横截面观察值的权重,非负的权重变量表示生产技术是规模报酬不变的。在模型中,合意产出和投入变量的不等式约束意味着合意产出和投入是自由可处置的。加上非合意产出的等式约束后,则表示合意产出和非合意产出是联合起来是弱可处置的。此外,为了表示产出的相互独立,需要对DEA模型强调下面两个条件:
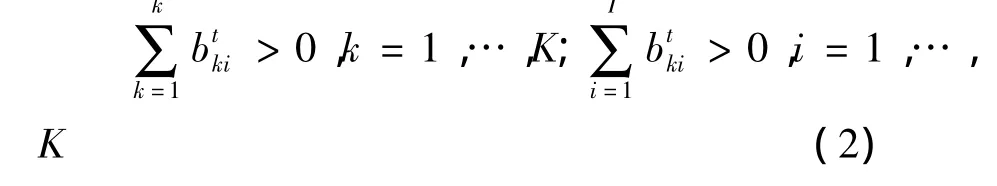
这两个条件分别表示每一种非合意产出至少有一个国家或地区生产、每一个国家或地区至少生产一种非合意产出。
尽管技术的构造有利于概念的解释,但是却无助于计算,为了计算碳排放管制下的全要素生产率,下面我们介绍方向性距离函数。
1.2 方向性距离函数
就像上文所提及,方向性距离函数主要目的是增加合意的产出,同时减少非合意的产出。方向性距离函数可以用下式表述:
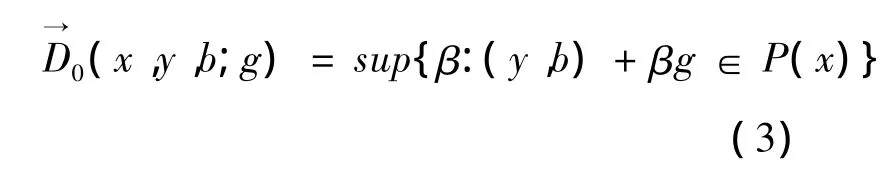
这里g是产出扩张的方向向量。按照Chung et al(1997),方向g=(y,-b)表示合意的产出增加,非合意的产出将会减少。传统的距离函数和方向距离函数的区别可以用图1表示。
在传统距离函数中,A点向前沿面C点移动时,合意产出和非合意产出同时增加,而在方向性距离函数中,A点向前沿面B点移动时,合意产出在增加而非合意产出在减少。在B点产出向量是(yt+ β*gy,bt- β*gb),在这里β*gy已加到合意的产出,而在非合意产出减去β*gy。
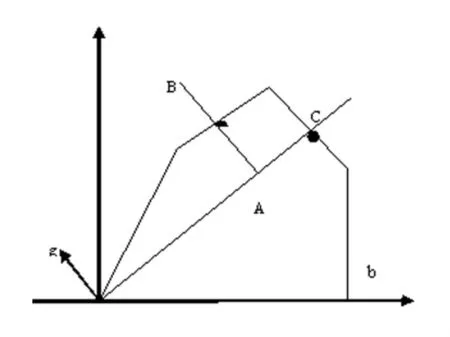
图1 传统产出距离函数和方向距离函数
1.3 Luenberger生产率指数(LPI)
LPI指数可以表示为:

Chambers et al.(1996)把LPI分解成效率变化指数(LEFFCH)和技术变化指数(LTECHCH),,这两个指数之和即为LPI指数。即:

1.4 DDF 的计算
假如要计算任意相邻两阶段方向距离函数和LPI指数,就要计算四个不同的距离函数,它们分别 是(xt,yt,bt;yt, - bt);D0t+1(xt+1,yt+1,bt+1;yt+1,- bt+1);D0t(xt+1,yt+1,bt+1;yt+1, - bt+1);(xt,yt,bt;yt,-bt)。以上四个方向距离函数分别用以下四个DEA模型来计算:


2 数据来源与说明
按照上述理论方法,我们需要中国工业内部各个行业1992年~2007年的合意产出、非合意产出和投入数。所需要的数据均来自1992、1997、2002、2007年中国投入产出表和中国能源年鉴,经过计算得到。首先,把1992年~2007年投入产出表转换为可比价的投入产出表。各个行业总产出为合意产出;非合意产出为各个行业二氧化碳的排放;二氧化碳的测算是根据中国能源统计年鉴工业各行业消耗各种能源分别乘以二氧化碳排放系数综合而来;投入分别为中间原材料和能源投入以及劳动力报酬。
表1描述了1992年~2007年期间二氧化碳排放和能源原材料消耗增长情况。从时间段来看,二氧化碳排放在2002年~2007年期间总体增长幅度较大,在这期间增长幅度最大的是电子及通讯设备制造业,增长幅度达到149.51%,其次是金属冶炼及压延加工业,增长139.58%,最低的是其他工业,增长仅为0.64%;在1992年~1997年期间二氧化碳排放增长幅度最小,而在1997年~ 2002年期间在不同行业波动较大,增长最高的金属冶炼及压延加工业,达到233.51%,而最低的是食品制造业,其二氧化碳排放下降幅度达到28.43%。从行业来看,二氧化碳排放增长幅度较大的是金属冶炼及压延加工业、电子及通信设备制造业、电气机械及器材制造业,增长幅度较小的行业有石油和天然气开采业、金属矿采选业、造纸及文教用品制造业等行业。能源与原材料消耗增长幅度最大的是在2002年~2007年期间,每个行业增长幅度均超过100%,在这期间增长幅度最大的是建筑材料及非金属矿物制品业,增长幅度达到271.99%,其他两个时间段增长幅度在行业间差异较大,增长最高的是电子及通信设备制造业,达到150%,最低的是建筑材料及非金属矿物制品业,下降34%。

表1 二氧化碳排放、能源原材料投入增长率的变化
3 模拟结果
影响二氧化碳排放的因素主要有技术进步、能源和原材料使用效率和经济增长。技术进步能够直接减少排放或者通过增加合意的产出对非合意产出比率间接较少二氧化碳排放。一般来说,在没有技术进步的情况下,经济增长会导致合意的产出和非合意的产出增加。相反,在经济下滑情况下,合意的产出和非合意产出均在下降。表2估算了在碳排放约束和传统的两种情况下,1992年~2007年期间工业各个行业的LPI指数的结果。
结果发现,在碳排放约束条件下,LPI指数在工业行业间差异较大,LPI指数增长最高的是其他工业达到6%,有三个行业LPI指数下降,分别是建筑材料及非金属矿物制品业、金属冶炼及压延加工业和金属制品业,其中下降幅度最大的是金属制品业,下降1.48%。如果不考虑二氧化碳排放的情况下,LPI指数增长最高的是缝纫及皮革制品业,增长幅度达到7.75%,有四个行业LPI指数下降,分别是建筑材料及非金属矿物制品业、金属冶炼及压延加工业、金属制品业和电气机械及器材制造业,其中下降幅度最大的是金属冶炼及压延加工业,达到4.3%。在结果中还可以发现,在二十一个行业样本中,有十一个行业考虑二氧化碳排放的LPI指数高于没考虑二氧化碳排放的LPI指数,有十个行业低于没考虑二氧化碳排放的LPI指数。
在分析碳排放约束下生产率变化原因时,我们把LPI分解成技术效率变化(LEFFCH)和技术变化(LTECHCH)。结果见表2。技术效率变化(LEFFCH)主要是在二氧化碳排放最小时工业技术扩散,这是由于使用较少的原材料,降低了燃料和能源利用、技术的改进以及管理和组织的结果。而技术变化(LTECHCH)主要是指使用创新的生产方法和吸收新技术,从而使生产前沿面外移。从表2的结果可知,在二十一个行业中,在考虑二氧化碳排放情况下,技术效率和技术进步均有改善的行业有九个,分别是煤炭采选业、石油和天然气开采业、金属矿采选业、其他非金属矿采选业、石油加工业、炼焦、煤制品业、化学工业、金属制品业和电力及蒸汽、热水生产和供应业。技术效率没有变化,而存在技术进步的行业有四个,分别是食品制造业、缝纫及皮革制品业、电气机械及器材制造业和仪器仪表及计量器具制造业。有一个行业技术效率没有变化,而存在技术退步,这个行业是建筑材料及非金属矿物制品业。有四个行业技术效率下降,而存在技术进步,这些行业分别是纺织业、机械工业、电子及通信设备制造业和其他工业。技术效率和技术进步均在恶化的行业是金属冶炼及压延加工业。
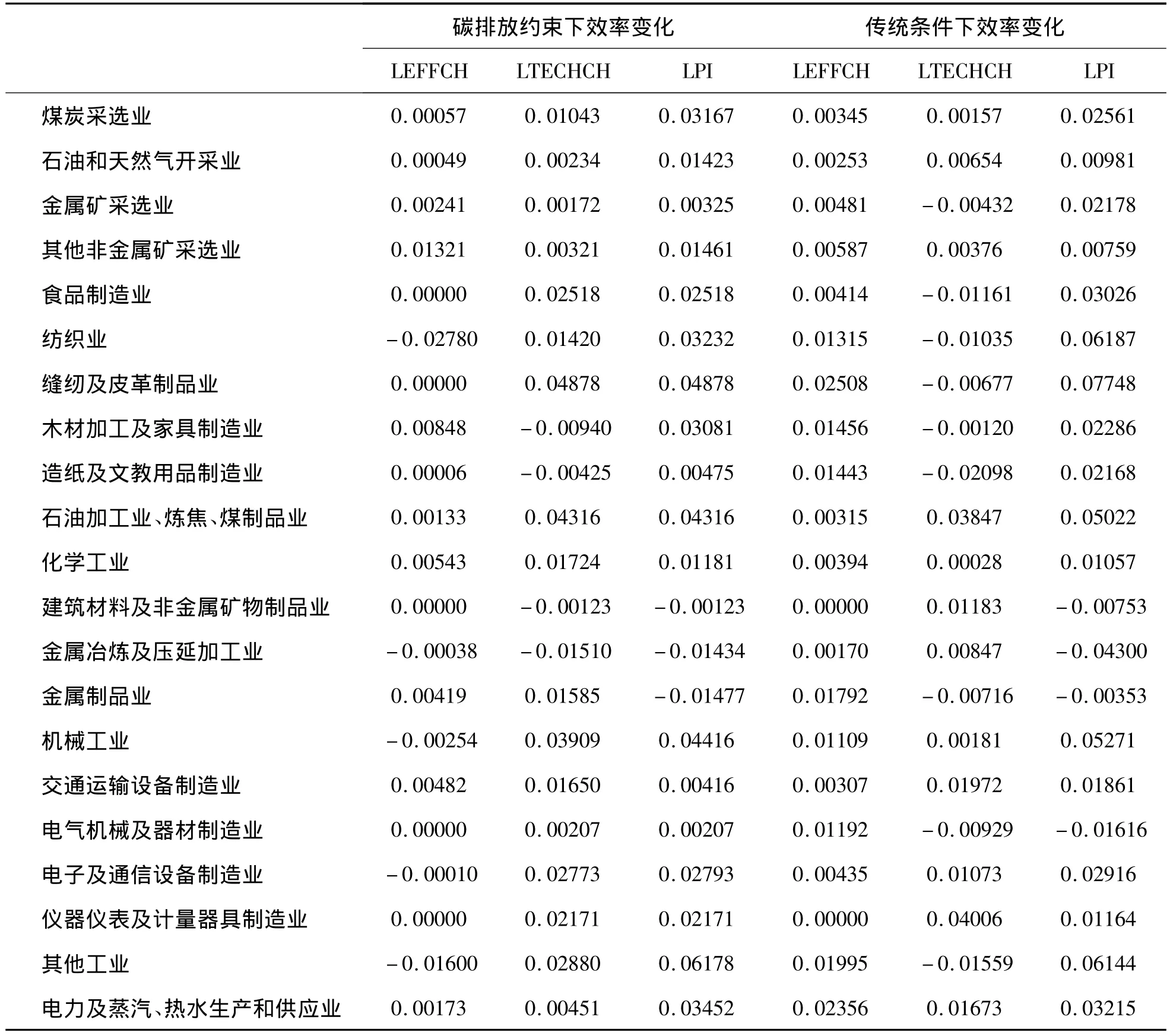
表2 1992年~2007年我国工业各行业效率分解
4 结论和政策建议
本文比较了在考虑二氧化碳排放和不考虑二氧化碳排放两种情况下,我国工业部门生产率增长,使用综合的方法把LPI分解成技术效率和技术进步增长来分析当二氧化碳排放达到最小时,全要素生产率增长。在1992年~2007年期间对二十一个工业行业使用非参数方向函数计算LPI,分析表明二十一个行业中有十一个行业考虑碳排放时LPI高于传统的LPI。研究发现,TFP的增长主要来源于技术创新,而不是效率的改进。结果表明,几乎所有的能源密集和原材料密集型的行业,不包括金属制品制造,具有更高效率和LPI指数。当考虑碳排放时,能源密集和原材料密集型的行业的全要素生产率主要是由于技术变革。
上述结论对于制定工业行业实现碳排放目标政策具有深刻的意义。首先运用碳排放约束下全要素生产率有效评估工业部门二氧化碳排放绩效,为工业部门建立节能减排监控体系提供依据;其次,研究表明,工业行业全要素生产率增长主要依靠技术创新,技术效率有待于改进,说明在实施节能减排过程中,不仅仅需要在节能减排“硬”技术方面进行创新、引进和吸收新技术,同时还需要提高管理水平和制度创新;最后,要实现经济又好又快发展,必须转变经济增长方式,促进工业结构调整,特别是降低原材料、能源部门的能源强度,提高能源消费效率。
[1]R,Grosskopf,s,Noh,D.Characteristics of a polluting technology:theory and practice[J].Journal of Econometrics,2005,126:469-492.
[2]Hailu,A.Veeman.Non-parametric Productivity Analysis with Undesirable Outputs:An Application to the Canadian Pulp and Paper industry[J].American Journal of Agricultural Economics,2001,83:605-616.
[3]Lindenberger,D.Measuring the Economic and Ecological Performance of OECD Countries[R].EWI Working Paper,2004.
[4]Domazlicky.B.Weber,W.Does Environmental Protection Lead to Slower Productivity Growth in the Chemical Industry[J].Environmental and Resource Economics,2004(25):301-324.
[5]Yoruk,B.K.,Zaim,O.Productivity growth in OEDE countries:a comparison with Malmquist productivity indexes[J].Journal of Comparative Economics,2005(40):401-420.
[6]Kumar,S.Environmentally Sensitive Productivity Growth:A Global Analysis Using Malmquis-Luenberger Index[J].Ecological Economics,2006(125):280-293.
[7]Caves,D.,Christensen,L.,and Diewert,W.The Economic Theory of Index Numbers and the Measurement of Inputs[J].Outputs and Productivity. Econometrica,1982,50(6):1393-414.
[8]Farre,R.,Grosskopf,S.Theory and Application of Directional Distance Functions.Journal of Productivity A-nalysis[J].2000(30):93-103.

