一种基于3-UPS并联机构的六维控制器运动学分析
肖 霄,宫金良,张彦斐
(山东理工大学机械工程学院,山东淄博255091)
在用户与计算机的交互过程中,鼠标是典型的二维控制器,通过它可以实现对计算机系统的各种操作,但是对于三维空间来说,它们并不太合适,因为三维空间中物体具有6个自由度,目前很难找出比较直观的办法把鼠标的平面运动映射成三维空间运动[1-3].然而随着科学技术的迅猛发展,对能够实现多自由度移动或转动控制的多维控制器需求越来越广泛,如虚拟现实技术、遥操作技术、计算机辅助设计、计算机三维动画设计以及数据可视化等,这些领域都需要一个多维控制设备来有效实现三维空间中物体的多自由度控制[4-5].基于文献[6] 提出的六维控制器设计方案,本文着重对其机械本体3-UPS并联机构进行运动学分析,从而为该六维控制器结构参数优化设计以及控制电路设计提供必要的理论依据.图1所示为3-UPS并联机构三维模型,它由动平台、静平台以及3个相同的UPS支链构成,其中虎克铰U由绕垂直于静平台平面的轴线和平行于静平台平面的轴线转动的两个转动副构成,且两轴线交于一点.图2给出了3-UPS并联机构的结构简图.
3-UPS并联机构的运动学分析包括两个方面:一方面是在已知机构几何参数和关节变量的情况下求解动平台相对于参考坐标系的位置和姿态,称为3-UPS并联机构的运动学正解;另一方面是在已知机构几何参数以及动平台相对于参考坐标系位置和姿态的情况下求解达到该位置和姿态时所需的关节变量,称为3-UPS并联机构的运动学反解[7].动平台的位置求解较为简单,而姿态求解较为复杂.通常用旋转矩阵、RPY角和欧拉角等来描述机器人末端姿态,由于采用旋转矩阵描述动平台姿态时需要9个参数,而采用RPY角和欧拉角描述只需要3个参数,同时欧拉角的所有转动都是相对于动坐标系描述的[8],这在计算机编程实现六维控制器虚拟控制时极为方便,因此本文将采用欧拉角来描述动平台相对于参考坐标系的姿态.
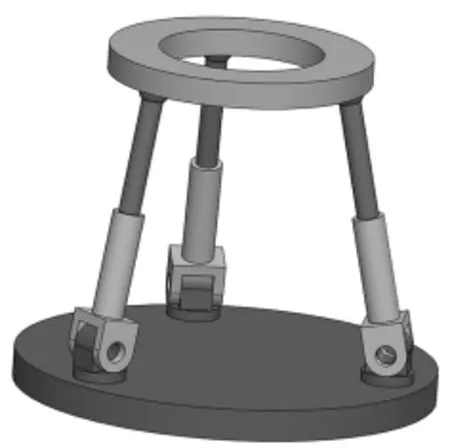
图1 3-UPS并联机构三维模型
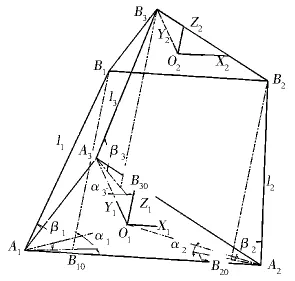
图2 3-UPS并联机构结构简图
1 3-UPS并联机构运动学正解
如图2机构简图所示,其中Ai(i=1,2,3)为构成虎克铰U两转动副中心轴线的交点,Bi(i=1,2,3)为球铰S的中心点,且A1、A2、A3及B1、B2、B3所围成的三角形均为等边三角形,设两等边三角形中心点分别为O1和O2,Bi0(i=1,2,3)为Bi在A1、A2、A3所确定平面上投影,li(i=1,2,3)为Ai、Bi两点间距离,αi(i=1,2,3)为AiBi在A1、A2、A3所确定平面上投影与AiO1所夹锐角,βi(i=1,2,3)为AiBi与A1、A2、A3所确定平面的夹角.为了便于分析计算,分别建立了如图2所示静坐标系O1X1Y1Z1及动坐标系O2X2Y2Z2,其中确立O1、O2分别为静、动坐标系原点,沿A1A2、B1B2方向为X轴方向,沿O1A3、O2B3方向为Y轴方向,过平台中心点且垂直于平台平面方向为Z轴方向.设Bi(i=1,2,3)在静坐标系中坐标为(xi,yi,zi),O2点坐标为(x,y,z).
设等边三角形A1A2A3边长为a,则A1、A2、A3在坐标系O1X1Y1Z1中坐标分别为:(-a/2,/6,0),(a/2,-/6,0),(0/3,0).又AiBi(i=1,2,3)在A1、A2、A3所确定平面上投影为AiBi0,且有‖AiBi0‖=licosβi,则由O1Bi0=(O1Ai+AiBi0)(i=1,2,3)可知B10、B20、B30在坐标系OX1Y1Z1中坐标分别为
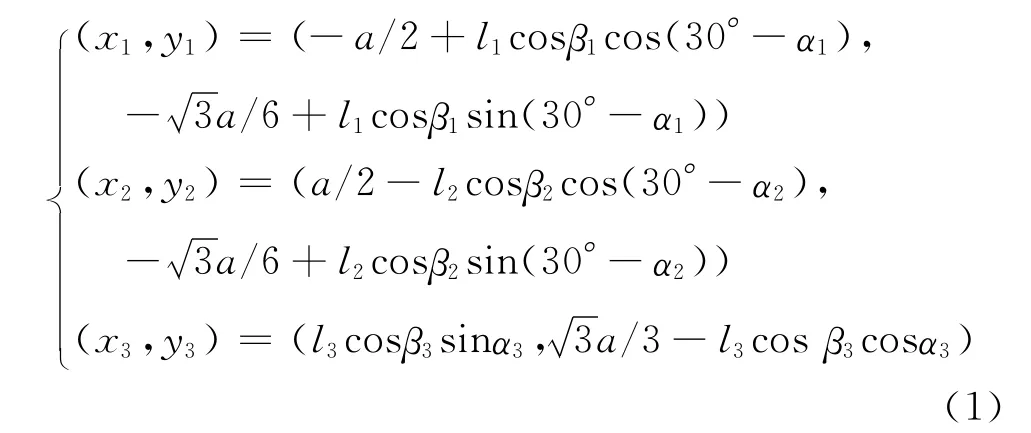
因为‖BiBi0‖=lisinβi(i=1,2,3),即zi=lisinβi,则O2点坐标为
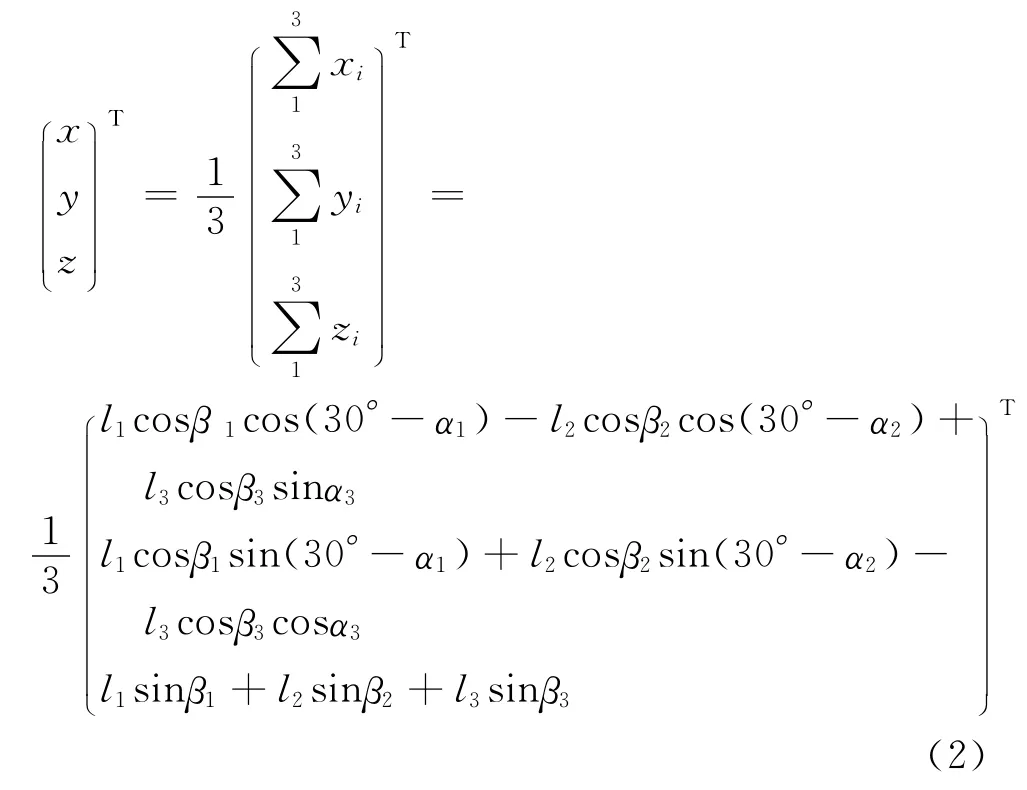
由机器人运动学知识可知,当用Z-Y-X欧拉角描述动坐标系时有

进一步,由式(3)可以逆解得到α、β、γ为

其中:

式(2)和式(4)即为3-UPS并联机构运动学正解.显然,当已知机构结构参数和关节变量时便可确定动平台的位置和姿态,当给定各关节变量变化范围时,便可求得动平台相对于参考坐标系的运动范围,也即六维控制器的工作空间,它是六维控制器操作性能评价指标之一.
2 3-UPS并联机构运动学反解
在求解3-UPS并联机构运动学反解时,动平台中心点坐标(x,y,z)以及α、β、γ为已知变量,而机构关节变量αi、βi、li为待求未知量.由坐标变换公式可知静坐标系O1X1Y1Z1中点与动坐标系O2X2Y2Z2中及存在以下关系:
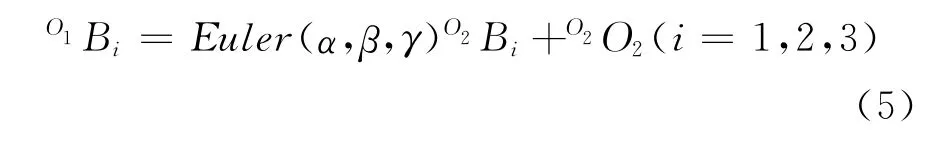
设等边三角形B1B2B3边长为b,则B1、B2、B3在动坐标系O2X2Y2Z2中坐标分别为:(-b/2,-,(b/2,-,(0
将坐标代入(5)式可得B1、B2、B3在静坐标系O1X1Y1Z1中坐标(xi,yi,zi)(i=1,2,3).
因为li=‖AiBi‖(i=1,2,3),则

进一步,由zi=lisinβi可得
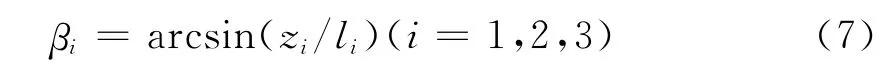
又由AiBi0(i=1,2,3)与X1轴夹角与其在X1轴上投影关系可以求解得到:
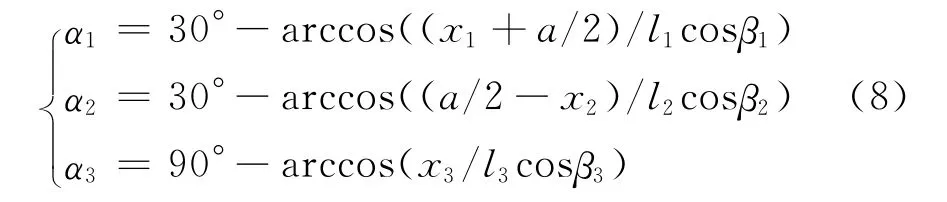
(6)、(7)、(8)三式即为3-UPS并联机构运动学反解,当已知动平台相对于参考坐标系的位姿时,便可确定各个运动关节的变量大小.由于六维控制器各关节变量通过安装在虎克铰U两转动副和移动副P处的传感器获得,因此3-UPS并联机构运动学反解对传感器量程及分辨率的选择具有很大的指导意义.
3 MATLAB仿真实例
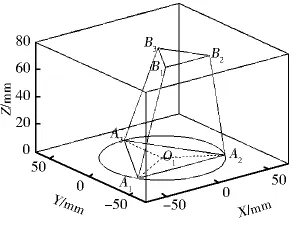
图3 沿X轴移动15mm
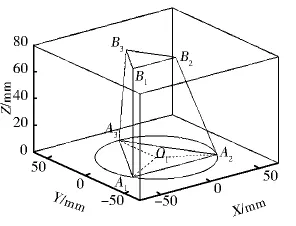
图4 沿Y轴移动15mm

图5 沿Z轴移动15mm
表1给出了3种不同机构位形时,根据运动学反解计算的对应关节变量.将关节变量重新代入正解计算公式,得到表2的位形参数.结果表明:与已知位形参数相比,误差均小于10-5,验证了机构正反解的正确性.
表1 a=时机构反解

表1 a=时机构反解
[x,y,z;α,β,γ] [α1,α2,α3,β1,β2,β3,l1,l2,l3] [0,0,70;0,0,0] [0.000,0.000,0.000,71.075,71.075,71.075,74.000,74.000,74.000] [15,0,70;0,0,0] [11.462,-34.264,32.005,61.667,79.225,67.986,79.527,71.256,75.505] [0,15,70;0,0,0] [-22.411,-22.411,0.000,64.045,64.045,82.674,77.852,77.852,70.576]
表2 a=时机构正解及误差

表2 a=时机构正解及误差
[__________________________________x,y,z;α,β,γ] δ_______[0.000,-1.184×10-15,70.000;0.000,0.000,0.000] ≤10-15[15.000,-2.768×10-5,70.000;-1.936×10-5,7.298×10-6,-7.093×10-6] ≤10-15[____________________0.000,15.000,70.000;0.000,-4.505×10-6] ≤10-6

图6 绕X轴转动15°

图7 绕Y轴转动15°

图8 绕Z轴转动15°
4 结束语
本文对六维控制器主体机构3-UPS并联机构进行了运动学分析,求出了其运动学正反解.通过运动学正解一方面可以求解机构工作空间,进而确定六维控制器可操作范围及操作灵活性,另一方面可以用于上位机虚拟环境中物体的控制,因此运动学正解的正确性尤为重要.为了验证正解的可靠性,本文采用MATLAB软件对机构进行了运动学仿真,仿真结果显示所求正反解是完全正确的.3-UPS并联机构的运动学分析为六维控制器结构参数优化设计以及控制电路的设计提供了理论依据.
[1] 梁秀波,张顺,李启雷,等.运动传感驱动的3D直观手势交互[J] .计算机辅助设计与图形学学报,2010,22(3):521-526.
[2] Huang C R,Chen C S,Chung P C.Tangible photorealistic virtual museum[J] .IEEE Computer Graphics and Applications,2005,25(1):15-17.
[3] 刘春,徐菁.一种数据手套交互控制模块的设计与应用[J] .计算机仿真,2009,26(3):251-255.
[4] 宫金良,张彦斐,周玉林,等.一种新型六维鼠标在虚拟现实技术中的应用[J] .传感器技术,2005,24(9):82-84.
[5] 赵现朝,高峰.并联机构的六维鼠标研制开发[J] .机械设计,2003,20(6):15-17.
[6] 宫金良,张彦斐,魏修亭.六维位置姿态传感器:中国,ZL200710114742.7[P] .2009-8-19.
[7] Hunt K H.Kinematic geometry of mechanisms[M] .New York:Oxford University Press,1978.
[8] 刘辛军,吴超,汪劲松,等.[PP] S类并联机器人机构姿态描述方法[J] .机械工程学报,2008,44(10):19-23.

