基于帕累托分布的洪水贝叶斯分析

黎协锐

（梧州学院数理系，广西 梧州 543002）

0 引言

研究汛期洪水水位的变化规律是应用水文学的一个重要内容，对洪水作出及时准确的预报预警是防洪减灾工作的关键，作为防汛斗争的“耳目”和“参谋”，为各级防汛抗旱部门正确作出防汛决策提供科学依据。洪水预报预警是预测江河未来洪水要素及其特征值的一门应用技术科学，是根据洪水形成和运动的规律，利用水文气象数据资料，对未来一定时段内的洪水发展情况进行预测预报分析，是防洪抗灾决策的重要依据，是一项重要的防洪非工程措施。根据洪水预报，可以事先对防洪工程(水库、闸坝)进行合理调度，及时拦洪、泄洪、削减洪峰，与下游区间洪水错峰，有效控制洪水。根据洪水预报，可以有计划地运用分蓄洪区拦蓄超额洪水，牺牲局部，保护全局，减少洪灾损失。根据洪水预报，可以事先组织群众进行防洪抢险，加高加固堤防，组织分洪区群众转移，保障人民生命财产的安全。一般的洪水分析模型往往注重现有的水文数据，对以往的水文统计资料利用得不够充分。运用贝叶斯分析方法不但可以充分利用现有数据信息，同时能有效应用以往的水文数据和结论，对洪水的变化规律作出更实时有效的预测预报。

1 基于帕累托分布的洪水贝叶斯分析

构建预报模型是洪水预报系统的核心，预报系统各模块均是围绕预报模型而开发的。因此根据不同情况研究各种洪水的预报模型，建立预报模型库，是进行洪水预报的最关键部分。目前在实时洪水预报方面，比较实用的是确定性概念模型。按照模拟的对象不同可分为河道汇流模型、流域产流模型、流域汇流模型、经验模型等。构建洪水预报模型的基本出发点是致力于提高洪水预报的精度，增长洪水预报的有效预见期，扩大预报范围，提高预报作业速度，为各级防汛抗旱部门提供预报精度和预见期均满足防洪调度决策要求的洪水预报成果。根据对我国重点防洪流域——珠江流域西江干流梧州水文站1949～2010年历次洪水洪峰水位数据的分析表明（如图1，其中18米为梧州水文站的洪水警戒水位，超过这个水位就会就成洪灾），洪水洪峰水位的分布可以看作是近似于右倾斜的分布，适合于用帕累托（Pareto）分布进行描述。帕累托分布最早是作为研究超过某一已知值λ的收入分布问题引进的，后来在研究城市人口分布，股票价格的起伏等问题中得到广泛应用。

图1 1949～2010年西江干流梧州文化站历次洪水水位排列

在防洪研究中，假设有n个独立的洪水洪峰水位观测值x=(x1,x2,…,xn)，他们来自帕累托分布

其中λ为尺度参数，θ为形状参数。在这里λ为成灾洪水水位值（超过这个值才会造成灾害，称为灾害洪水），θ为未知参数，研究洪水水位大于λ的问题。假定我们开始时对参数θ的信息是分散的或不明确的，采用Jeffrey先验分布来表示这种状况的先验信息，即

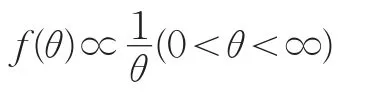
似然函数为：

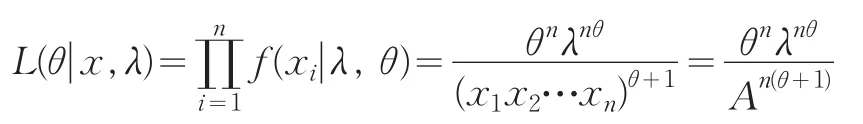
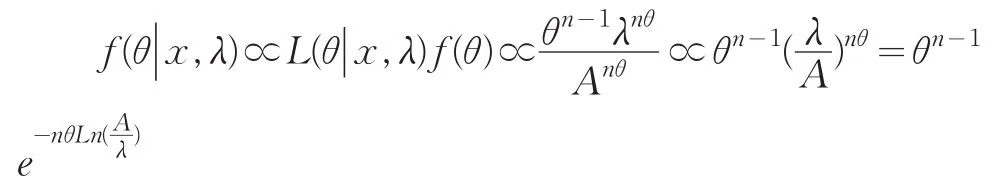
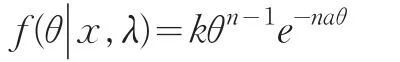
对后验分布密度正则化

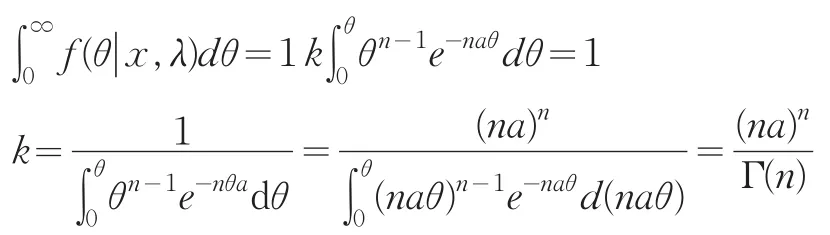
从而得到参数θ的后验密度为

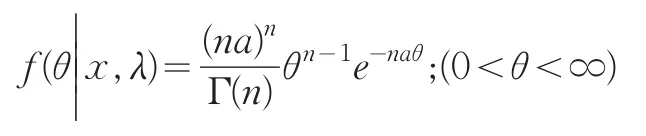
这个基于样本观测值x1,x2,…,xn和Jeffrey先验分布的θ的后验分布代表了对有关θ的认识，我们可以计算c1＜θ＜c2的后验概率

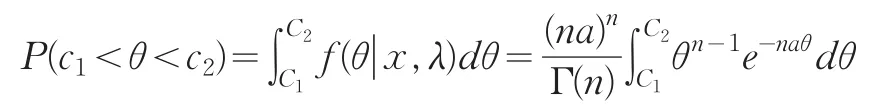
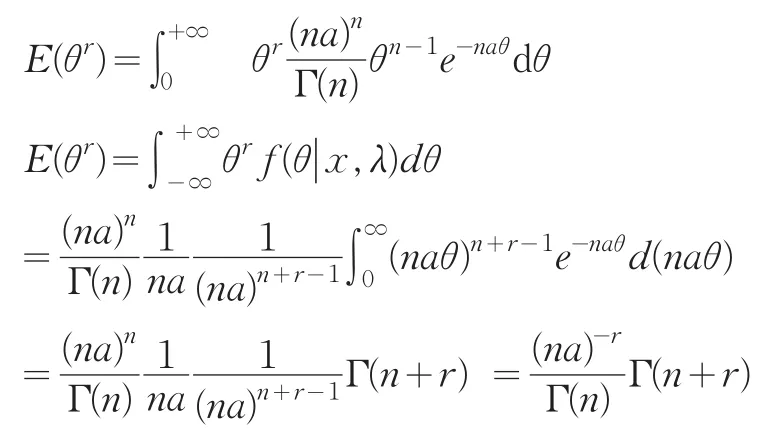
特别地

可以用这个作为参数θ的最优估计点。而洪水水位x落入某区间λ＜a＜x＜b的概率为

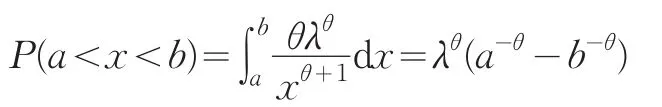
如果我们另有m个独立观测值的新样本x*=(x*1,x*2,…,x*m)，它们也都来自帕累托分布

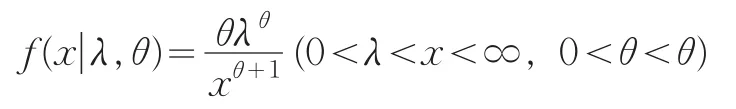
其中A*为m个新观测值的几何平均。利用贝叶斯定理将上面的先验分布和似然函数合并，基于两组数据的后验分布为

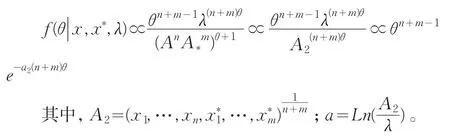
这同样是Γ分布的形式。依次类推，这样不断地根据最新的观测数据利用贝叶斯定理对历史数据进行修正，从而得到实时的预测结果。

2 实际问题中的处理

在实际研究中，利用帕累托分布进行分析时,一般不是直接利用个别的观测值x1,x2,…,xn,更多的是利用频率n0,n1,…nt,nt+1,…,nT，如历年洪水水位落入特定区间xt到xt+1的频数nt，这里x0=λ;t=0, 1, …,T。洪水水位x落入某区间xt＜x＜xt+1的概率为

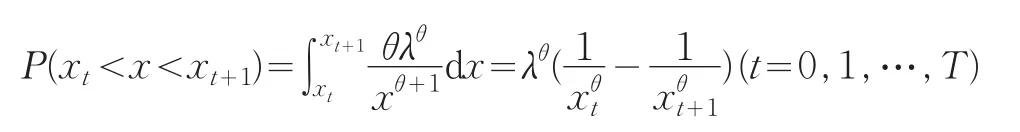
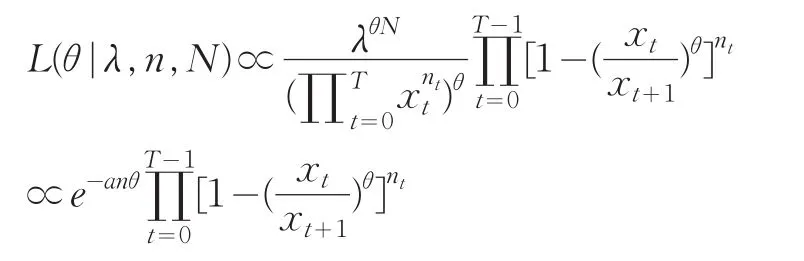
给定θ的先验分布f(θ)，利用贝叶斯定理与似然函数合并得后验密度

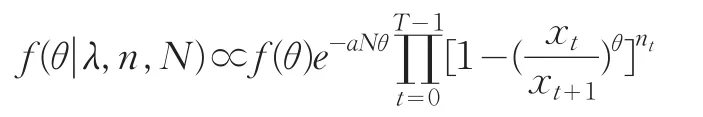
如果没有太多的信息可用，先验分布f(θ)同样可采用Jeffrey先验分布的形式，即

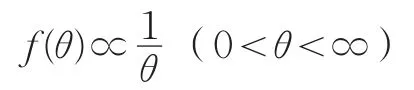
这时θ的后验密度为

其中，k为正则化常数；

如果有足够多的先验信息可用，f(θ)就采用可代表它的形式，同样对后验密度正则化即可计算出有关参数和进行需要的计算。

表1、表2给出了我国主要的防洪区域之一西江流域梧州水文站1949～2010年的汛期（6～8月）水文数据进行分析，这里共收集了122次洪水的数据，即有122次洪水的水位大于成灾水位λ=18米。

表1 1949～2010年西江干流梧州水文站历次洪水水位频率分布

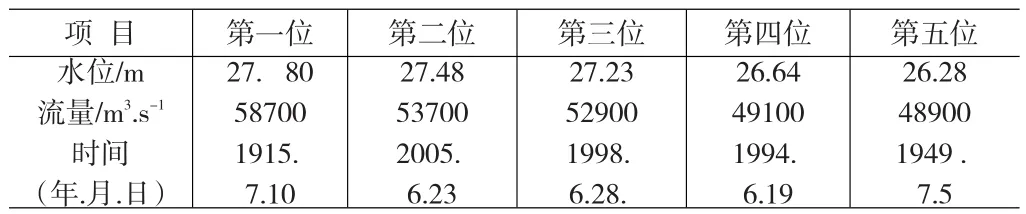
表2 洪水排序表

3 结论与对策

虽然洪水预报在防洪减灾中发挥着重要作用，但现有的预报模型距离防洪减灾的高要求仍有差距，主要表现在预见期较短、部分项目精度不高、预报范围较少等方面。

一是洪水预报预见期较短。较长的洪水预见期是做好防洪调度决策、生命财产安全转移的前提。目前，我国大部分洪水预报预见期小于2天，有的甚至只有几个小时，致使防洪调度决策仓促，生命财产转移不及时。如长江荆江分洪区的运用需要24小时的决策、转移时间，而目前做出其调度依据沙市站的洪水预报预见期只有9个小时左右，远远满足不了分洪调度要求。

二是有些预报项目精度有待提高。预报精度是做好防洪调度决策的另一重要因素，而尤以水位预报精度最为重要。特别是防洪重点地区的大江大河中下游水位预报精度，表现在流量精度较高，而通过水位流量转换后的水位预报却满足不了要求。如2003年淮河洪水期间，王家坝闸是否分洪需要高精度的洪水预报，为使蓄滞洪区人员和财产安全转移需要更长时间的预见期；在1998年长江、松花江、嫩江大洪水期间，各级领导和防汛部门需要高精度的干流水位预报来组织抗洪抢险，甚至要求误差在0.05m范围内，大大高于水文情报预报规范的要求。

三是预报范围满足不了防汛抗旱的要求。目前，开展的预报范围较少，一般只注重大江大河、重要防洪地区的洪水预报，而随着国民经济的发展，防汛抗旱工作的拓展，大江大河的支流、非重点防洪地区的防洪任务日益繁重，迫切需要开展洪水预报工作；同时开展的预报项目较少，注重洪水预报，而对径流、旱情、山洪、水环境预报关注不够。

在洪水预报的实践中，由于预报对象所处的河段、流域和洪水千差万别，根据站点类别、信息种类不同，造成预报模型因预报对象不同而不同，因此根据具体情况构建不同的预报模型并建立足够的模型库是解决问题的关键。如美国天气局河流预报系统（NWSRFS）具有包含28个常用的预报模型的预报模型库，用户可任意选择所需模型用于构建预报方案。

[1]朱慧明，韩玉启.贝叶斯多元统计推断理论[M].北京：科学出版社,2006.

[2]茆诗松.贝叶斯统计学[M].北京：科学出版社,1999.

[3]马超群，罗劲虎,杨艳.Gamma分布参数多个转变点的Bayes推断[J].湖南大学学报（自然科学版）,1999,（3）.

[4]黎协锐.一个概率变点问题的Bayes估计[J].梧州学院学报,2007,（6）.

[5]高延红.基于实测年最高洪水位的现有堤防加高设计的洪水位分析[J].中国农村水利水电,2006,（9）.

[6]黎协锐.基于Bayes估计理论的洪水水位概率变点研究[J].统计与决策,2009,（21）.