液压缸用带锁口杆端关节轴承瞬态动力学分析

苏高峰，薄玉成，王惠源，孔静静 ，徐煜星

(1.中北大学 机电工程学院，太原 030051；2.台州科锦轴承有限公司，浙江 台州 317000)

关节轴承属于球面滑动轴承，其旋转轴线可绕球面的中心作大空间大范围摆动。按关节轴承承受的载荷方向、公称接触角和结构形式的不同，可分为向心关节轴承、角接触关节轴承和推力关节轴承；按是否附有杆端或装于杆端上，分为一般关节轴承和杆端关节轴承；按工作时是否需补充润滑剂，分为自润滑型关节轴承和润滑型关节轴承[1]。关节轴承作为通用机械零件，由于能满足重载荷、长寿命、转动灵活、可调心、少维护、结构紧凑及易于装拆等特点，已被广泛地用于矿山、冶金、电力、交通、水利电力、航天航空和纺织等领域中。带锁口杆端关节轴承主要用于机械同心度要求不高，工作表面压力较大且又要做低速摆动、倾斜(即调心运动)或回转的机械机构中。本例以QG325 型切管机液压缸用带锁口杆端关节轴承为研究对象，通过三维软件Solidworks建立简化的带锁口杆端关节轴承模型，利用有限元分析软件ANSYS Workbench对其进行结构瞬态动力学分析，分析结果表明带锁口杆端关节轴承最薄弱的部位与以往的经验相一致，为改进该轴承的结构设计、调整装配布局提供了理论依据。

1 结构特征和受力分析

某公司生产的内螺纹带锁口GIHN-K32LO型杆端关节轴承可用于QG235型切管机液压缸的摆动支承中。轴承由外圈、内圈和杆端体组成。外圈装在杆端体中，内圈与轴颈相配，轴颈摆动带动内圈在球面上摆动。轴承基本参数[2]：内圈宽度32 mm，内圈直径32 mm，外圈宽度18 mm，调心角4°；径向游隙0.05～0.10 mm；聚四氟乙烯润滑脂；额定动载荷67 kN。滑动摩擦副为钢/钢。

在切管机工作的过程中，安装在液压缸顶端的带锁口杆端关节轴承通过轴颈承受径向载荷Fr和轴向载荷Fa。由轴颈带动轴承内圈上下摆动，使切管机的切刀盘上下移动切割钢管。杆端关节轴承主要受径向载荷Fr=50 kN，也受一定的轴向载荷Fa=6 kN,其当量径向载荷[2-3]

Q=Fr+yFa

(1)

式中：y为轴向载荷系数。由Fa/Fr=6/50=0.12，查表[3]得y=0.8，则得Q=54.8 kN。

2 瞬态动力学分析基本算法

ANSYS Workbench中有两种求解运动学方程的方法，即模态叠加法和直接积分法，具体如图1所示。

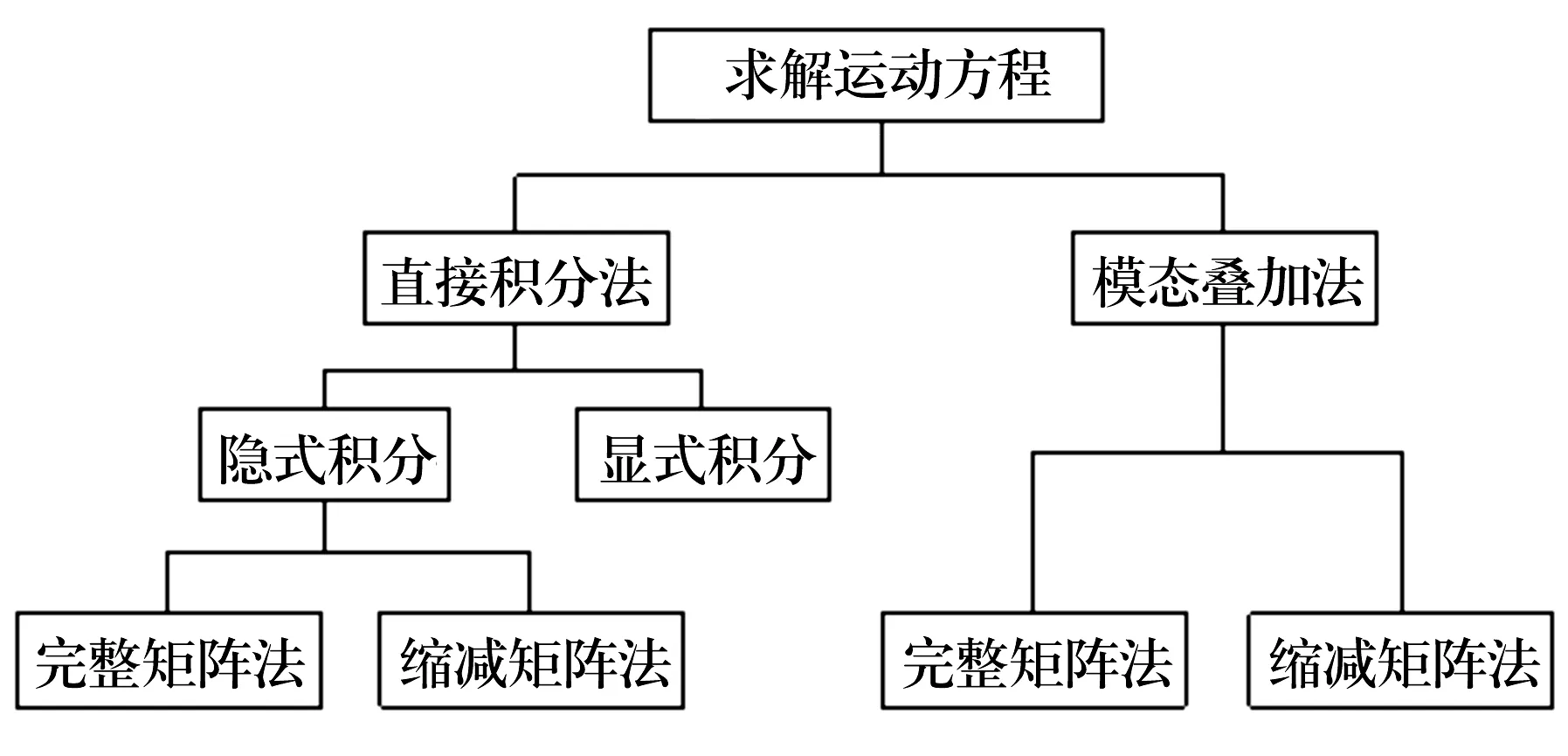
图1 运动学方程求解方法流程图

瞬态动力学分析(也叫时间历程分析)是用于确定结构承受任意随时间变化载荷的结构动力学响应。可以用瞬态动力学分析确定结构在稳态载荷、瞬态载荷和简谐载荷的随意组合下随时间变化的位移、应变、应力及力。载荷和时间的相关性使得惯性力和阻尼作用比较重要。如果惯性力和阻尼作用不重要，就可以用静力学分析代替瞬态分析[4]。输入数据的一般形式是载荷为时间的任意函数；输出数据为随时间变化的位移和其他的导出量，如应力和应变。ANSYS Workbench允许在瞬态动力分析中包括各种类型的非线性-大变形、接触和塑性等等。其基本运动方程为

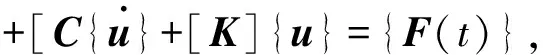
(2)

3 有限元仿真模型

3.1 几何模型的建立

首先根据二维图纸用三维造型软件Solidworks建立带锁口杆端关节轴承的三维实体模型。鉴于杆端体几何形状的复杂性， 为了有效地进行有限元结构建模， 根据圣维南局部作用的原理，对一些圆角、倒角等细部特征进行了删除或抑制工作； 而对远离主要受力部位杆端体圆角区域的几何特征, 在保留整体刚度基本不变的条件下, 对结构进行了适当简化， 简化后的带锁口杆端关节轴承结构如图2所示。 对于关键部位，尤其是严重影响受力状态的部位，则保留其结构上的倒角及圆角等，以保证瞬态动力学分析结果的真实性。

图2 带锁口杆端关节轴承简化的三维模型

3.2 材料模型

由于轴承塑性变形很小，因此将轴承内、外圈和杆端体均设为线弹性材料。在仿真模型中，假设内、外圈材料均为GCr15钢，密度为7 830 kg/m3，弹性模量为206 GPa，泊松比为0.3；锻件杆端体材料为45#优质碳素结构钢，密度为 7 850 kg/m3，弹性模量为196 GPa，泊松比为0.24。

3.3 网格划分[5]

根据模型的特点，采用扫略分网与3D几何网格相结合的方式划分网格。带锁口杆端关节轴承内、外圈采用六面体单元，杆端体采用四面体单元；假设轴承工作时内圈连接在刚性很大的轴上，外圈固定在杆端体上，因此将内圈内表面和外圈外表面设置为固定约束；模拟轴承的边界条件， 内、外圈和杆端体均设置为柔性体，以便施加摆动运动副和载荷。 轴承有限元模型如图3所示，共有65 650个单元，111 880个节点。

图3 带锁口杆端关节轴承网格图

3.4 边界条件和载荷的设置

杆端体与大地、关节轴承外圈和杆端体均设置为固定副，内、外圈之间设置为转动副，动摩擦因数0.04，外圈外表面设为全约束，假设轴承在工作中承受54.8 kN的载荷，通过ANSYS Workbench13.0的新增功能创建表面印记。表面印记仅用来分割体上的面，但不创建新几何体，这样就可以把轴承内圈分为上下4个各为1/4内圈面积的区域。压力简化为均布施加的力，参照文献[6]，可以设置时间历程为40.0 s，0～20.0 s假设为向下摆动轴承的工作行程，在内圈下半面的前半部分上均布施加F1=54.8 kN的力，在上半面的后半部分均布施加F2=54.8 kN的力；20.001～40.0 s假设为向上摆动轴承的工作回程，在内圈下半面的后半部分均布施加F3=54.8 kN的力，在上半面的前半部分也均布施加F4=54.8 kN的力。载荷-时间变化方案如图4所示，图中x为轴向，y为垂直径向，z为水平径向。

图4 载荷-时间变化方案图

4 仿真结果分析

4.1 三维应力分析

根据上述有限元模型和边界载荷条件，得到带锁口杆端关节轴承最终仿真结果和最大应力时程曲线图如图5、图6所示。从图5可以看出，轴承较大的Von Mises应力出现在内圈边缘凹槽处、外圈油孔附近和单开缝处、杆端体与外圈接触的下半圈内侧区域。

轴承上、下摆动过程中随着承载区的变化最大应力值及最大应力位置都将发生变化。如图6所示，带锁口杆端关节轴承的最大应力值并不是时刻不变的，由于各种复杂的原因，最大应力在工作行程和回程刚开始的一段时间内存在稍许波动，然后才趋于稳定，其中内圈边缘凹槽是轴颈作用在内圈上的应力集中部位，其应力变化最为剧烈。因此，仅仅从应力方面看，内圈是带锁口杆端关节轴承中受应力冲击最大和最容易受损的零件。应力最大值出现在轴颈与内圈接触表面以下一定深度区域，并逐渐向外衰减。Hertz接触理论认为，在带锁口杆端关节轴承这样的圆接触区内将形成压应力，压应力值沿曲面的轴向和法向变化，并且应力最大值出现在一定深度(20 .7 μm)上的仿真计算结果与Hertz理论分析结果一致。

图5 三维Von Mises应力分布云图

时间/s

4.2 位移和速度变化分析

ANSYS Workbench窗口中能清楚地表征带锁口杆端关节轴承各物理量在时间域上的变化过程，图7所示为带锁口杆端关节轴承上下摆动的X方向的位移和速度时程曲线图。

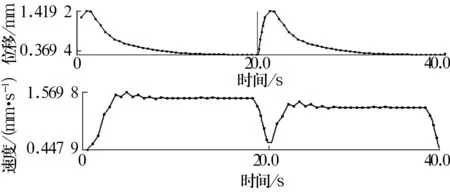
图7 X方向的位移和速度时程曲线图

从图中可以看出，轴承位移和速度时程曲线具有明显的周期性，周期的长短和载荷的大小与作用时间密切相关。从速度时程曲线可知，由于径向游隙的存在，使内、外圈并不是时时刻刻紧靠在一起，存在速度的微小波动，这也是带锁口杆端关节轴承在工作过程中内、外圈多次相接触而产生磨损，使径向游隙变大而影响运动精度及产生噪声的主要原因。可以通过位移和速度时程曲线图判断结构设计和装配布局的合理程度，为改进提供参考。

5 结论

(1)带锁口杆端关节轴承内部的最大应力出现在轴颈与内圈接触表面以下一定深度区域，并逐渐向外衰减，仿真计算结果与Hertz理论分析结果一致。

(2)在带锁口杆端关节轴承各零件中，内圈边缘凹槽为应力最大处，其次为外圈油孔和单开缝附近及杆端体与外圈接触的下半圈内侧区域。

通过对QG325型切管机液压缸带锁口杆端关节轴承进行瞬态动力学分析, 得到了实际工况下带锁口杆端关节轴承的受力云图。通过分析受力云图可知, 最大应力离材料的屈服极限还有一定的盈余, 说明材料没有发生屈服, 但经过多次循环工作容易出现疲劳破坏和磨损。最大应力出现的部位和以往的经验相一致, 说明所建立的有限元分析模型能够较真实地反映该轴承的受力状态。采用有限元仿真的方法可以模拟带锁口杆端关节轴承在实际工况下的应力分布状态, 可为改进带锁口杆端关节轴承的设计和/或调整装配布局提供理论依据。