高速铁路轴箱轴承载荷分布分析
颜家森,朱龙泉,赵三星,宋世勇,王凤才,,3
(1.武汉科技大学 机械自动化学院,武汉 430081;2.瓦房店轴承集团有限责任公司 国家大型轴承工程技术研究中心,大连 116300;3.西安交通大学,西安 710049)
伴随着高速铁路的快速发展,对高速铁路列车的性能要求愈来愈高。轴箱轴承作为高速铁路列车最重要、最关键的核心部件,其关键技术的研究有着重大的意义[1-2]。目前,高速铁路列车轴箱轴承多为双列圆锥滚子轴承。这种双列圆锥滚子轴承的工况与技术要求较一般同类型轴承有着明显的不同,它不仅需要承受较大的径向载荷,还要承受一定的轴向载荷;更重要的是能够运行在较高的速度水平上,并有较高的可靠性,避免任何因素导致的失效[3]。文中基于高速铁路轴箱用双列圆锥滚子轴承的实际工况,建立拟动力学模型,分析工作状态下轴承的载荷分布及外部载荷和列车运行速度等对轴承载荷分布的影响。
1 轴承的力学模型
双列圆锥滚子轴承的具体参数见表1,轴承中滚子素线为对数曲线。

表1 轴承的几何参数
轴承中的滚子处在承载区时,滚子推动保持架旋转;滚子处在非承载区时,保持架推动滚子旋转,运动情况较复杂。这里的分析暂不考虑保持架的影响,单个滚子与套圈的运动学关系如图1所示。
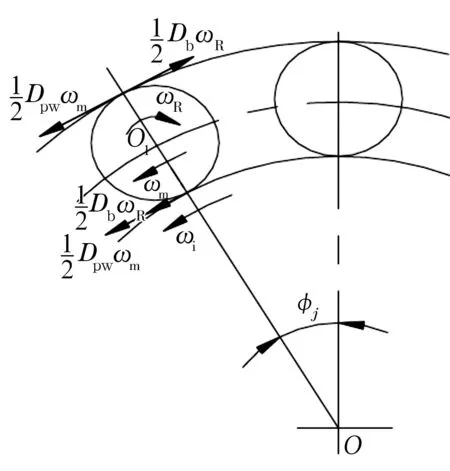
图1 滚子与内、外圈的运动关系图
在轴承旋转过程中,外圈与车箱箱体配合,外圈的绝对转速可设置为零,而内圈与传动轴转速相同。设列车运行速度为v0,车轮直径为Dr,轴的转速为n0,φj为滚子的方位角,根据滚子内部运动关系有
(1)
(2)
式中:ωi为内圈转动角速度,ωi=2πn0=2v0/Dr;ωm为滚子公转角速度;ωR为滚子自转角速度。由(1)和(2)式可以求得滚子的公转角速度和自转角速度,为分析滚子的动力学提供参考。
轴承在稳定运转时,可以认为滚子是平衡的(忽略滚子的歪斜情况)。利用拟动力学方法分析滚子受力平衡时,考虑滚子的离心力和陀螺力矩作用,单个滚子受力分析如图2所示。

图2 双列圆锥滚子轴承的滚子受力分析
滚子的力和力矩的平衡方程为
Qmfjsinαf+Qmijsinαi-Qmejsinαe=0,
(3)
Qmejcosαe+Qmfjcosαf-Fcj-Qmijcosαi+
Fmc2j-Fmc1j=0,
(4)
Mj-Qmfjs=0,
(5)
(6)
(7)
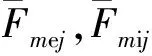
Fmc1j和Fmc2j相对于滚子与套圈的接触力极小,可以忽略不计。对(3)~(4)式进行求解,得Qmij=CiQmej,Ci=λsin(αe+αf)/sin(αi+αf),λ为修正系数,与Fcj和Qmej的值有关。这样得出滚子与内、外圈的接触载荷之间的关系。
对于对数曲线修形的圆锥滚子,当其锥角不大时,由经典Hertz接触理论可推导出滚子与外圈间接触载荷和变形之间的关系[4]
(8)
式中:K为滚子与外圈接触的总刚度系数;δmnj为滚子与外圈间的接触变形量;下标n表示滚子接触线法线方向。
由于内、外滚道的接触角不同,圆锥滚子轴承中滚子与内、外圈间的接触变形不同,因此滚子总的接触变形不能由以上两个变形简单相加而得到[5]。故以滚子与外圈间的接触变形为参照,将滚子与内圈间的接触变形向与外圈接触的法线方向投影,将该投影与滚子和外圈间的接触变形相加,即可得到滚子总的接触变形。对于双列圆锥滚子轴承,外圈为一个整体,两个内圈与外圈配合成为一个轴承整体系统,将两个内圈视为一个整体,这样内圈相对于外圈的整体位移仍定义为径向位移δr和轴向位移δa。考虑初始径向游隙Gr,以图3中的载荷和位移方向为参照,定义每一列滚子φj=0的位置,使滚子接触变形量增加的位移为正位移,反之则为负位移。不考虑套圈的弯曲变形时,在方位角为φj的滚子处,沿外滚道接触法线方向的总位移为
δ1nj=[δrcosφ1j-0.5Gr(1-cosφ1j)]cosαe+δasinαe,
(10)
δ2nj=[δrcosφ2j-0.5Gr(1-cosφ2j)]cosαe-δasinαe。
(11)
实际计算滚子与外圈之间接触载荷时,不一定每个滚子都受载,没有受载的滚子与外圈的接触载荷为零,那么在计算前必须首先做出判定,如果δmnj≤0,则这些不受载的滚子与套圈的接触载荷为零,即Qmej=0。
Qmej在Fr和Fa方向上的分量分别为
Qmerj=Qmejcosαecosφmj,
(12)
Qmeaj=Qmejsinαe。
(13)
在考虑整套轴承受力平衡时,以内圈-滚子为受力对象进行分析,暂不考虑整套轴承承受的弯矩,其受力如图3所示。

图3 轴承内圈-滚子受力示意图
整套轴承的受力平衡方程为
(14)
式中:Fr,Fa分别为轴承承受的径向力和轴向力。这样就建立起了高速铁路轴箱轴承的拟动力学模型。
2 数值模拟方法
双列圆锥滚子轴承滚子载荷分布受径向力、轴向力、轴承转速、温升、润滑和轴承几何精度等因素的影响。联立上述方程可以解得双列圆锥滚子轴承的径向位移δr和轴向位移δa,采用Newton-Raphson法来求解,可以得到轴承的载荷分布,进而分析外部载荷和列车运行速度对轴承载荷分布的影响。
3 分析及讨论
高速铁路每节列车车厢空载为12 t,满载重量为17 t,每节车厢由4根轴传动,8套轴承支承。在列车转弯时,取一定的运行速度和轨道半径可计算其承受的离心力为重力的0.2~0.3倍,此离心力为轴承所受的轴向力。该双列圆锥滚子轴承安装后有初始径向游隙0.065 mm。图4为列车运行速度300 km/h,轴承承受径向力21 kN,轴向力4 kN时,第1列滚子分别与外圈、内圈和内圈挡边的接触载荷Qe,Qi和Qf的分布图;图5为第2列滚子分别与外圈、内圈和内圈挡边的接触载荷Qe,Qi和Qf的分布图。外部载荷对滚子受载情况的影响如图6~图8所示。

图4 第1列滚子的受载情况

图5 第2列滚子的受载情况
由图4和图5可以看出,所有滚子的接触载荷对称分布。对比图4和图5可以发现,第1列滚子有15个滚子受载,第2列只有7个滚子受载,第1列滚子的最大接触载荷为第2列滚子最大接触载荷的3.8倍,其他相对应位置第1列滚子的接触载荷比第2列的都大。由于轴向力的存在,整套轴承主要由第1列滚子承受载荷,大约承受90%的载荷。对于第1列滚子,当滚子处在方位角φ=0处时,滚子与外圈的接触载荷最大为3.23 kN,与内圈的接触载荷值为3.1 kN,两者相差2.8%。当滚子所处方位角大于130°时,滚子与外圈的接触载荷为零,此时滚子进入非受载区;滚子方位角在0~130°时,接触载荷随方位角的增大而减小,表明滚子在旋转过程中承受交变应力。对于第2列滚子,受载区范围要比第1列小53.3%。两列滚子与内圈挡边存在接触压力,分布情况与Qe相同,最大值为Qe的4%,尽管数值不大,但会使滚子与内圈挡边之间产生摩擦。
图6为列车从空载到满载,轴向力4 kN,列车运行速度300 km/h时,该轴承第1列滚子与外圈的接触载荷变化图。图6a表明,随着径向力的增大,滚子最大接触载荷线性增大;从图6b可以看出,φ=0处滚子的接触载荷随径向力的增大而增大,从2.6 kN增加到3.2 kN。但随着径向力的增大,不是每个滚子的接触载荷都增大,方位角在90°~120°的滚子的接触载荷反而变小;同时,随着径向力的增大,承载的滚子数将减少,从15粒减少为13粒,滚子承受的载荷向上半圈集中。这是因为下半圈滚子与外滚道的接触载荷的方向与径向力方向相反,当径向力增大时,由于径向载荷的作用会使上半圈滚子的变形加大,而下半圈滚子与外滚道的接触变形会减小,接触载荷也减小。因此,最大接触载荷随着径向力的增大而增大,承载区反而随径向力的增大而减小。
轴承承受轴向力0~6 kN,径向力20 kN,列车运行速度300 km/h时,第1列滚子与外滚道的接触载荷如图7所示。由图7a可以看出,滚子的最大接触载荷随轴向力的增大而线性增大。图7b表明,随着轴向力的增大,受载滚子的数目从9粒增加到了15粒,承载区明显变大。方位角φ=0处滚子的接触载荷从1.9 kN增大到了3.6 kN;方位角φ=51.42°处滚子的接触载荷随轴向载荷的增大率为0.277 0;方位角φ=85.7°处滚子的接触载荷随轴向载荷的增大率为0.261 3,3个数值基本接近,可见轴向载荷线性增大时,所有滚子的接触载荷也基本为线性增大。
列车运行速度直接决定轴承的转速,轴承的转速又决定滚子的离心力和陀螺力矩。图8给出了列车运行速度0~300 km/h,径向力20 kN,轴向力4kN时,第1列滚子与外滚道的接触载荷。由图8a可知,列车运行速度从0提高到300 km/h,最大接触载荷只增大了25 N,增幅为0.8%;图8b显示,随着列车运行速度的提高,其余方位角不为零的滚子的接触载荷基本保持不变,即列车运行速度对此种载荷下轴承的载荷分布影响不大。这是因为轴承在承受重载时,由于旋转产生的离心力与外部载荷相比很小,所以其对滚子的受载影响很小。

图6 径向力影响载荷图
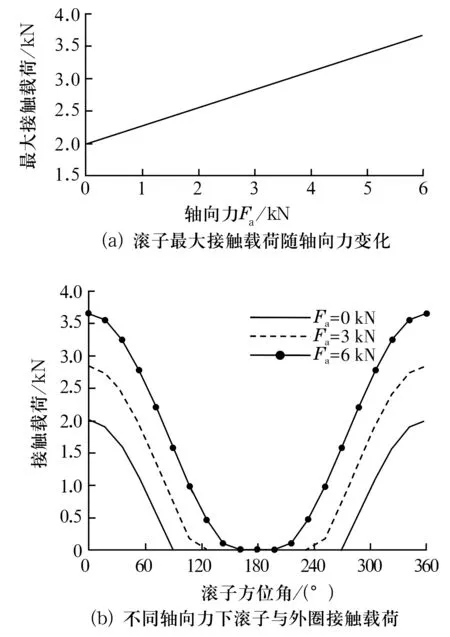
图7 轴向力影响载荷图
由于列车运行速度对此类轴承的载荷分布影响不大,那么在考虑轴承受力时可以忽略动载荷的影响,用静力学分析的方法即可。
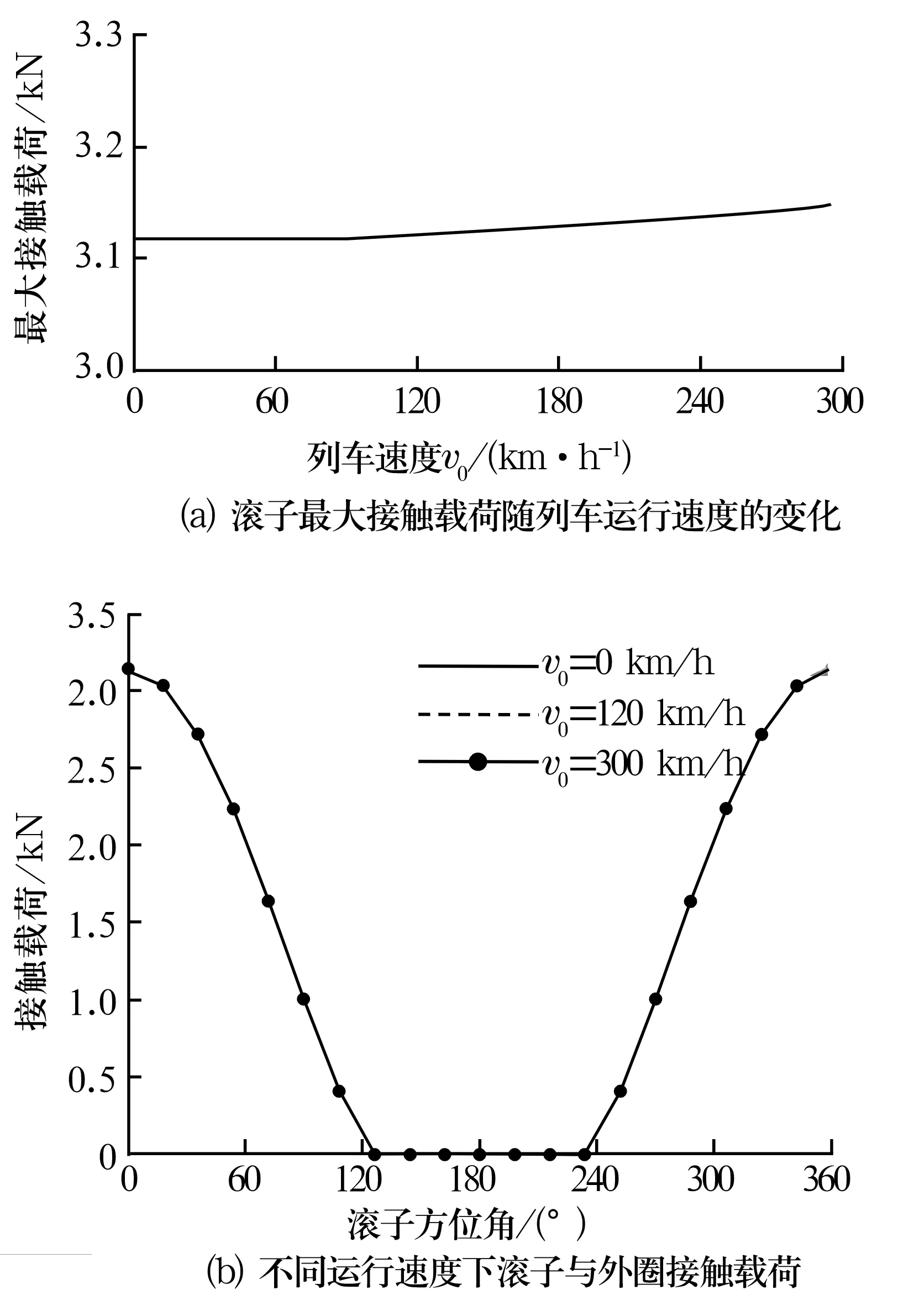
图8 列车运行速度影响载荷图
4 结束语
建立了双列圆锥滚子轴承的拟动力学分析模型,求解了稳态下轴承的载荷分布,分析了外部载荷和列车运行速度对载荷分布的影响。当轴承承受混合载荷时,受压列的滚子承受绝大部分载荷,第2列承受小部分载荷。滚子方位角越大所受接触载荷越小,各滚子在旋转过程中承受交变应力,这对于研究其疲劳特性和寿命有很大帮助。最大接触载荷随径向力和轴向力线性增大,所有滚子的接触载荷与轴向力基本呈线性关系,受载区域随轴向力的增大而增大,随径向力的增大而减小。轴承在承受较大载荷时,列车运行速度对滚子接触载荷的大小和分布影响不大。对于此类高速铁路轴承采用静力学分析即可。

