滚动轴承-转子系统动力学特性分析
魏彬,李建华,邓四二
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳轴研科技股份有限公司,河南 洛阳 471039)
作为转子的重要支承部件,滚动轴承的动态特性直接影响转子系统的动态性能。国、内外学者在转子系统的研究方面做了大量研究工作。文献[1-2]研究了滚动轴承支承的平衡转子和不平衡转子的动力学行为,并给出了轴承径向游隙对转子系统动力学行为的影响规律。文献[3-4]从轴承的游隙、波纹度及不平衡力等因素对转子系统动力学进行研究,指出轴承的变刚度频率特性对系统动力学特性有着显著的影响,当轴承变刚度频率与转子固有频率相等或外圈波纹度阶数与滚动体数目相等时都会引起转子系统的共振。文献[5]分析了转速和轴承游隙对不平衡弹性转子动力学响应的影响。文献[6]基于ADAMS研究了变载荷作用下计入轴承游隙时弹性转子-滚动轴承系统的动力学问题,结果表明:转子的弹性和轴承游隙对转子系统的动力学特性影响很大。上述研究均是基于将支承轴承简化为弹簧和阻尼的滚动轴承-转子动力学研究,没有考虑滚动轴承动力学特性和转子动力学特性的耦合问题。鉴于此,文中在滚动轴承动力学[7]和转子动力学[8]基础上,建立滚动轴承-转子系统非线性动力学微分方程,采用Newmark-β积分法和Newton- Raphson迭代法对轴承-转子非线性动力学微分方程进行求解,就轴承结构参数和工况参数与轴承-转子系统的动力学特性关系进行理论分析。
1 动力学分析模型
轴承-转子系统简图如图1所示。支承轴承B1,B2为角接触球轴承,外圈固定不动,内圈旋转,内圈与转子紧配合。轴承承受的预紧力为Fa;转子系统承受径向载荷Fr作用,其作用点在转子质心位置。系统坐标系坐标原点位于转子质心,x向为轴向,y向为垂直方向,z向为水平方向。
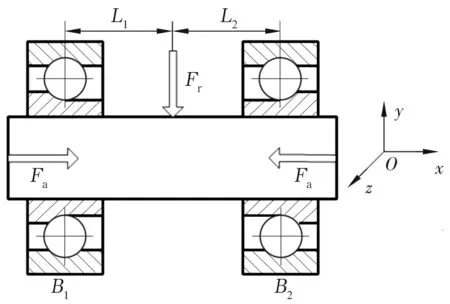
图1 轴承-转子系统示意图
1.1 轴承动力学模型
角接触球轴承在使用时为了提高其支承刚度,一般对其进行轴向预紧。角接触球轴承在轴向预紧力Fa作用下,钢球与沟道间的接触角变化示意图如图2所示。预紧力与接触角的关系为
(1)
式中:α0为轴承原始接触角;α为预紧后的轴承接触角;Kn为载荷-变形常数;Z为钢球个数;BDw为内、外沟曲率中心的原始距离。
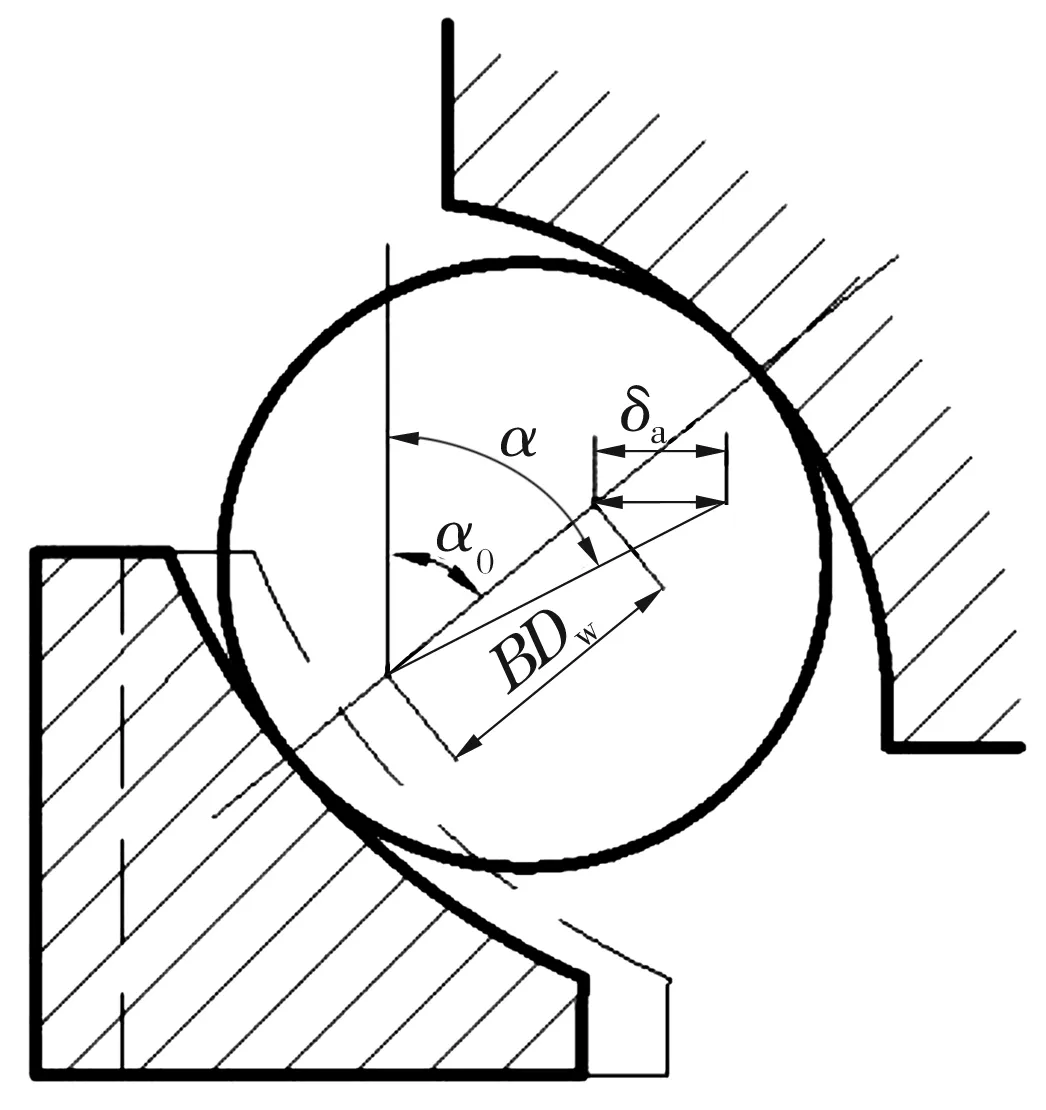
图2 预紧力作用下轴承接触角变化示意图
预紧后钢球和轴承内、外圈间的接触变形与接触角之间的关系为
δ=BDw(cosα0/cosα-1) ,
(2)
联立 (1)和(2)式即可求得在预紧力作用下轴承的接触角。
角接触球轴承所受载荷为通过转子作用于内圈上的外力,即轴承对转子支承力{Fx,Fy,Fz,My,Mz}的反力以及轴向预紧力。图3为角接触球轴承在所受载荷作用下钢球和套圈间的接触角、变形与位移几何关系图。设轴承内圈位移为{Δx,Δy,Δz,θy,θz}。图3中x向表示轴承轴向方向;r向表示轴承径向方向;Ob为位移后钢球中心;O1为外沟道沟曲率中心;O20为位移前内沟道沟曲率中心;O2为位移后内沟道沟曲率中心;Dw为钢球直径;φj为第j个钢球的方位角;R1(2)为沟道曲率中心到轴承轴线的径向距离;f1(2)为沟道沟曲率半径系数;α1(2)j为钢球与沟道的工作接触角,下标1表示外沟道,下标2表示内沟道。
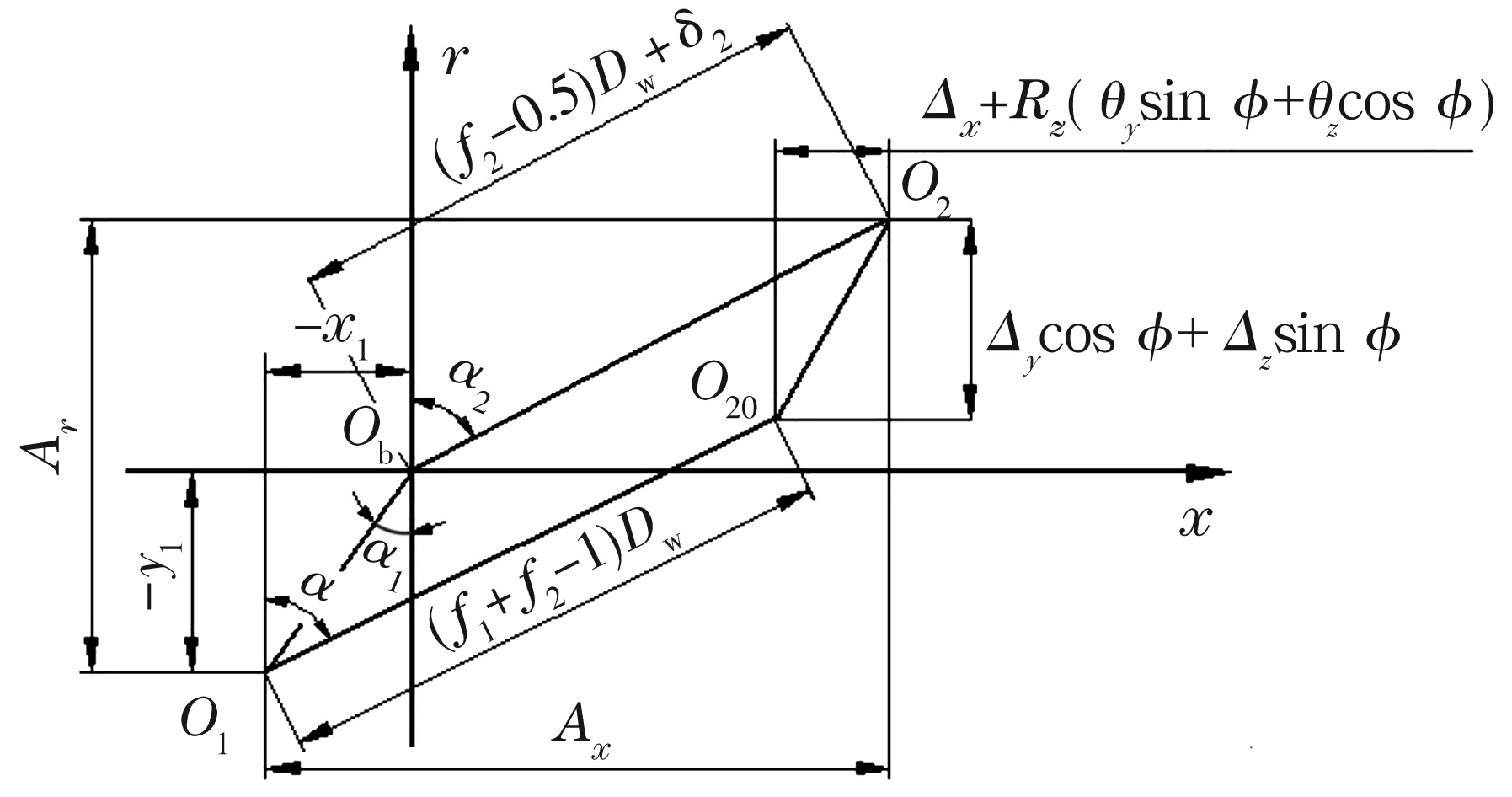
图3 接触角、变形和位移几何图
由图3几何关系可得
Axj=[(f1+f2-1)Dw]sinα+[Δx+R2(θy·
sinφj+θzcosφj)]=[(f1-0.5)Dw+δ1j]sinα1j+[(f2-0.5)Dw+δ2j]sinα2j,
(3)
Arj=[(f1+f2-1)Dw]cosα+(Δycosφj+Δzsinφj)=[(f1-0.5)Dw+δ1j]cosα1j+
[(f2-0.5)Dw+δ2j]cosα2j。
(4)
由(3)和 (4) 式可得钢球与内、外圈的接触变形量和工作接触角为
(5)
α1j=arctan(x1/r1)j,
(6)
(7)
α2j=arctan[(Ax-x1)/(Ar-r1)]j。
(8)
1.1.1 钢球动力学微分方程
第j个钢球的受力情况如图4所示。具体求解公式见文献[9]。根据Newton运动定律及Euler运动方程,第j个钢球的动力学微分方程组如下
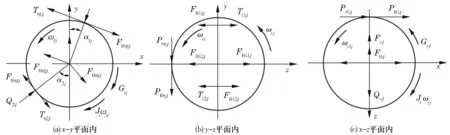
图4 钢球受力图

,(9)
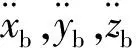
1.1.2 内圈动力学微分方程
轴承内圈的动力学微分方程组为
,(10)
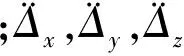
1.1.3 保持架动力学微分方程
图5为保持架的受力图。保持架的动力学微分方程组为
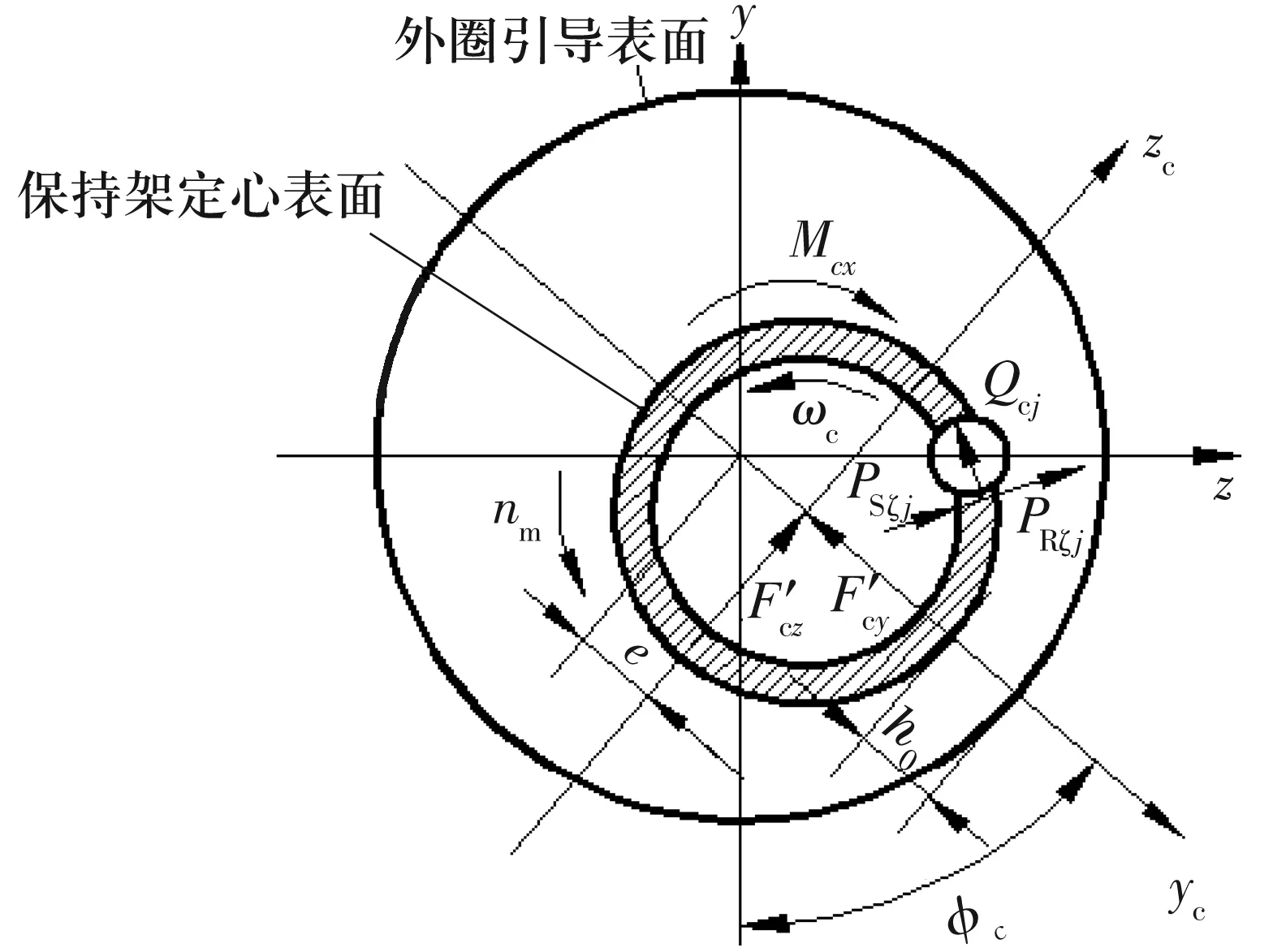
图5 保持架受力图
(11)
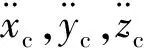
1.2 转子动力学微分方程
假设转子转速不随时间变化,根据Newton运动定律及Euler运动方程,转子的动力学微分方程组为
(12)
式中:m为转子质量;Fr为作用于y方向的径向力;Δx,Δy,Δz为转子质心位移;Fx,Fy,Fz为轴承对转子的支承力;下标1,2分别代表轴承B1,B2;Ix,Iy,Iz为转子转动惯量;θy,θz为转子角位移;My,Mz为轴承对转子的支承力矩。
1.3 系统中存在的振动频率
系统中包括两个不同的振动频率,一个是转子的转动频率,可表示为
(11)
另一个是支承轴承的变刚度频率[10],这是由于钢球依次通过承载区,轴承径向刚度不相等产生的,可表示为
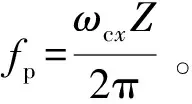
(12)
2 动力学特性分析
以某动量轮轴承组件中的轴承-转子系统为例进行计算。由于轴承内圈与转子紧配合,假设内圈位移和转子位移一致,以转子的振动位移作为初始条件,采用Newmark-β积分法和Newton-Raphson迭代法对轴承-转子非线性动力学微分方程进行求解。转子直径为10 mm,L1=L2=11.5 mm。轴承主要参数为:外径26 mm,内径10 mm,宽度8 mm,初始接触角15°,钢球直径4 mm。
2.1 轴承参数对系统动力学特性的影响
在支承轴承预紧力80 N,转子径向载荷200 N,转速4 000 r/min的工况下,分析轴承结构参数对系统动力学特性的影响。
2.1.1 内、外沟曲率半径系数的影响
图6、图7分别为不同内、外沟曲率半径系数时转子质心的振动频率响应。从图中可以看出:转子质心的振动频率响应由一个主峰和若干个次峰组成,说明转子系统是非线性系统。其频率响应仅有转子的转动频率及其倍频与亚频,转子的转动频率对应的幅值最大,说明转子的转动频率在系统的振动中占主导地位。内、外沟曲率半径系数的变化对转子振动特性的影响很小。
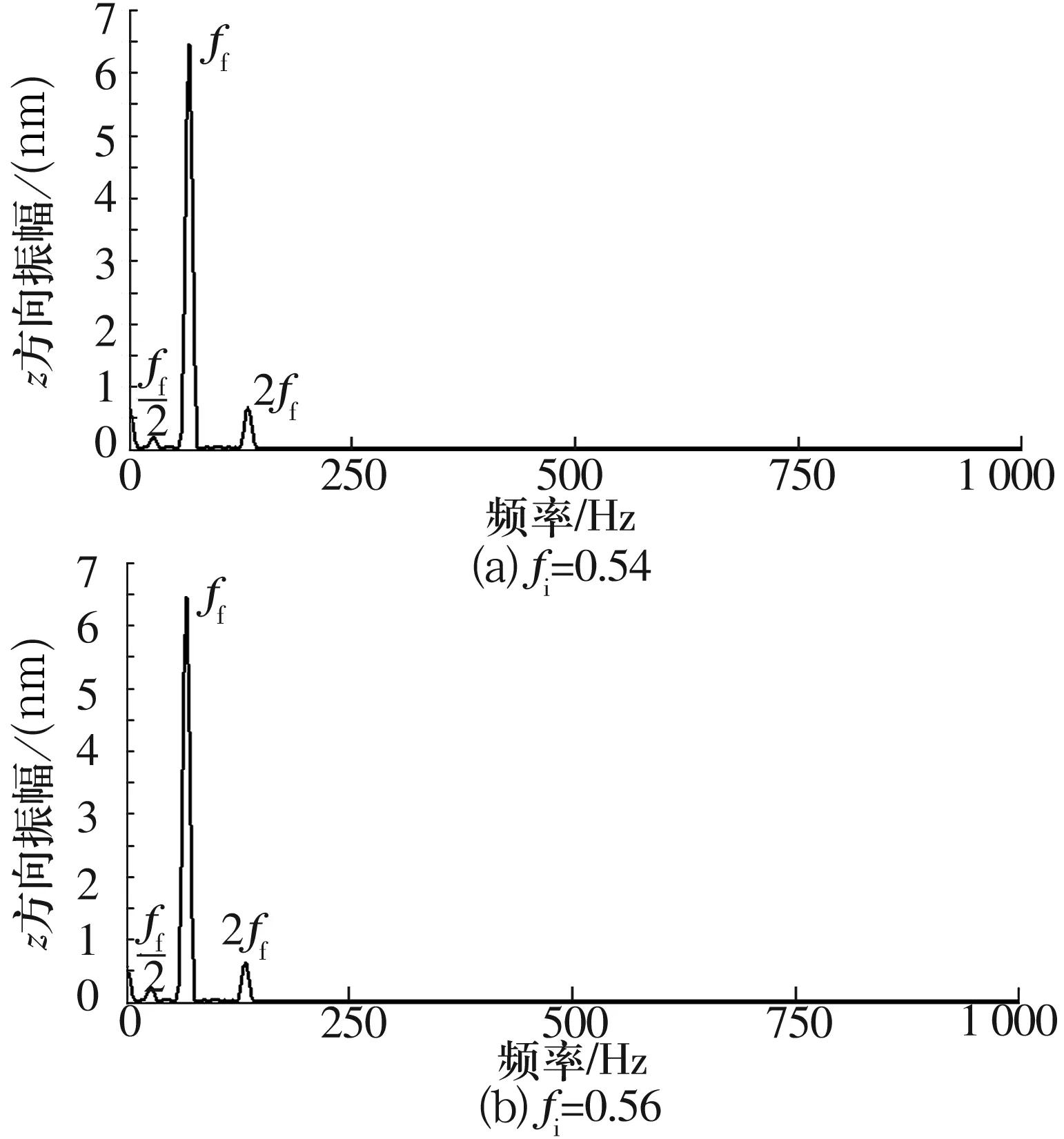
图6 不同内沟曲率系数时转子质心的振动频率响应
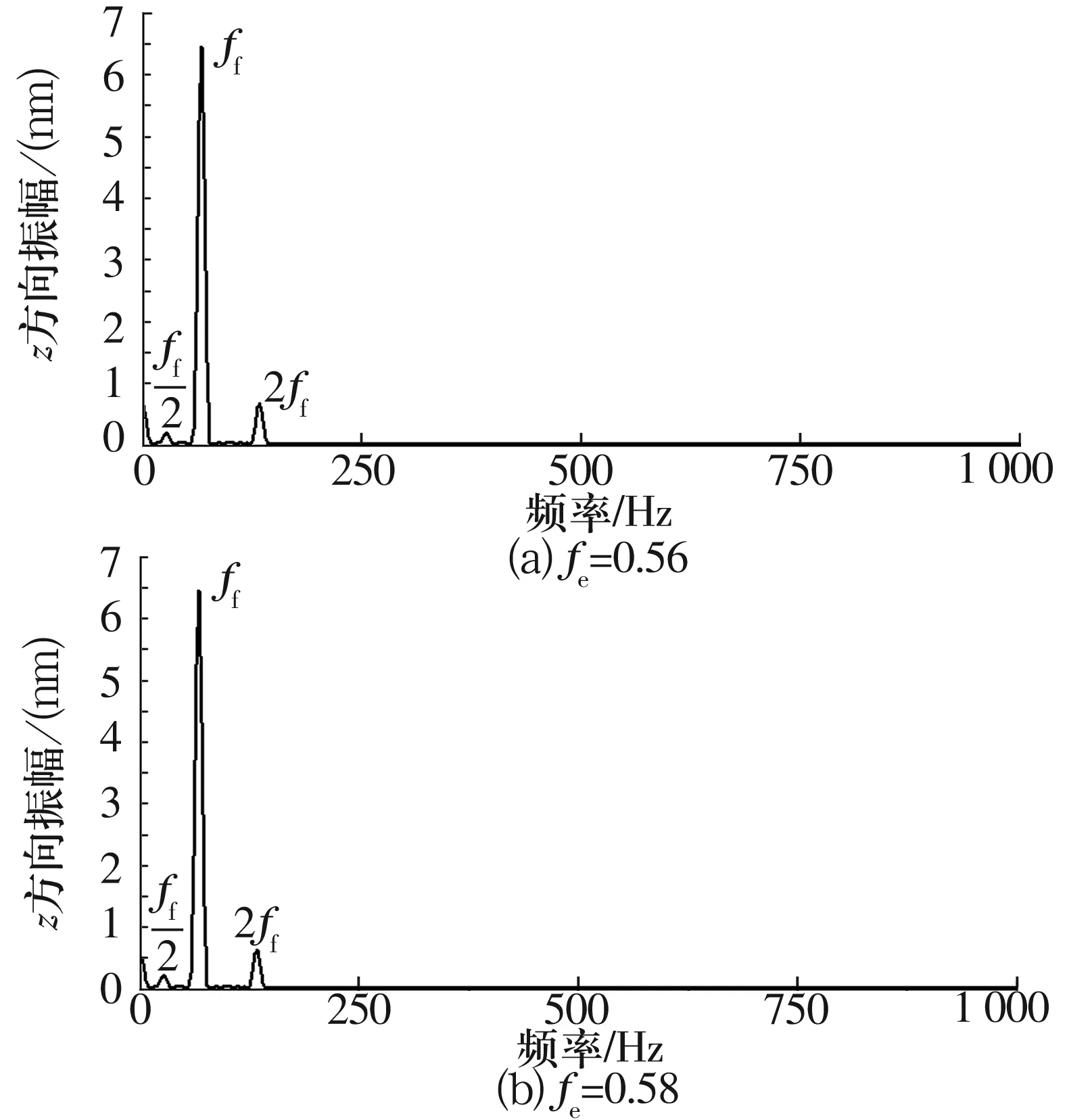
图7 不同外沟曲率系数时转子质心的振动频率响应
2.1.2 钢球个数的影响
图8所示为支承轴承不同钢球个数时转子质心的振动频率响应。由图8可以看出:钢球个数较少时,转子质心的振动频率响应中不仅存在转子的转动频率及其倍频与亚频,还存在支承轴承的变刚度频率及其倍频,转子的转动频率和轴承的变刚度频率同时起主导作用。随着钢球个数的增加,虽然轴承的变刚度频率增大,但在转子质心的振动频率响应中轴承的变刚度频率及其倍频逐渐消失,且变刚度频率及其倍频对应的幅值减小,说明系统的非线性特性减弱。但增加钢球数,就要相应增加保持架的兜孔个数,这会使保持架梁变薄,导致保持架早期失效。故须在保证保持架刚度的前提下,选取较多的钢球数,以减弱转子系统的非线性。
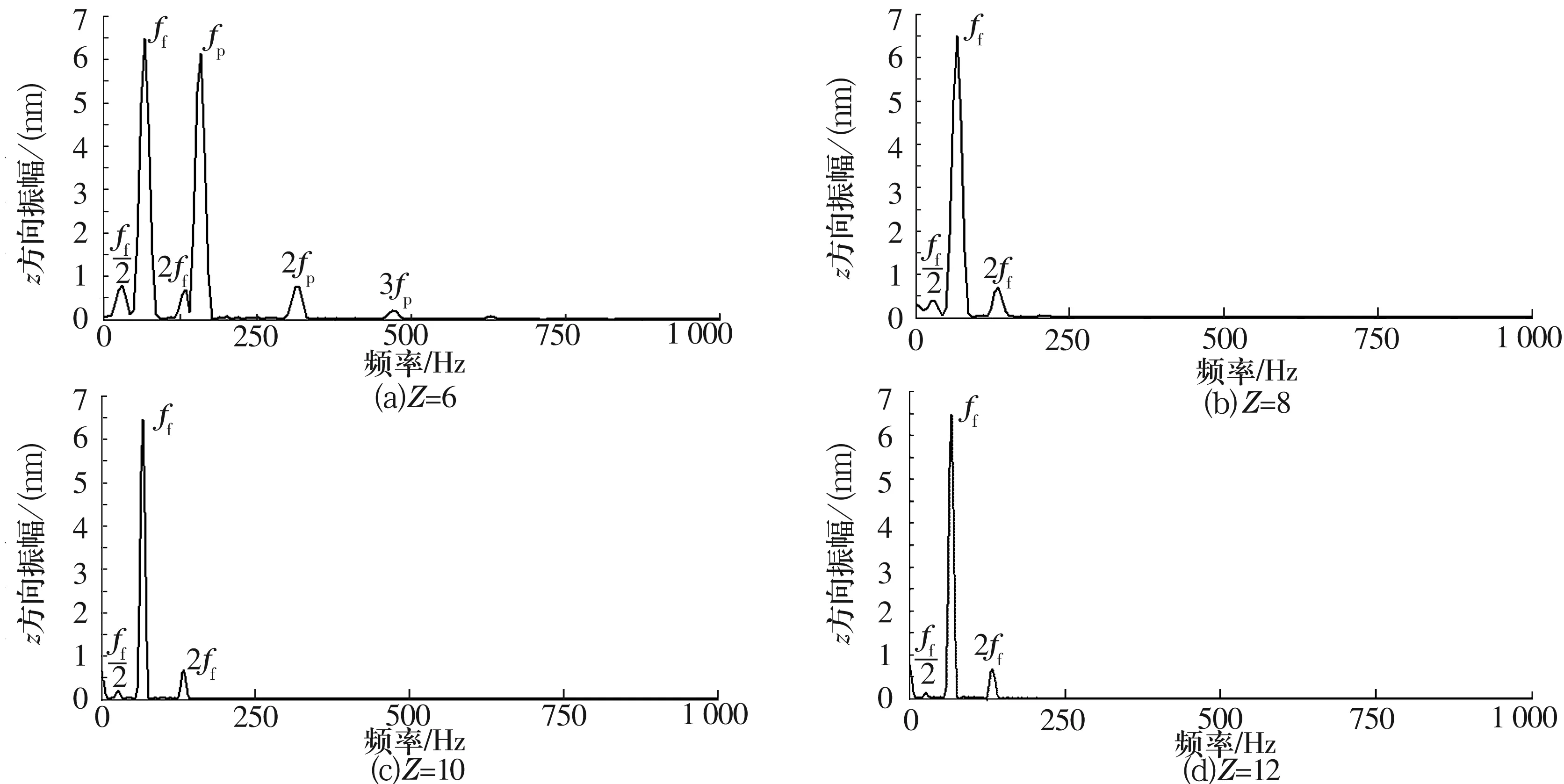
图8 不同钢球个数时转子质心的振动频率响应
2.2 工况参数对系统动力学特性的影响
2.2.1 预紧力
图9为不同预紧力时转子质心处的振动频率响应。可以看出:轴承的轴向预紧力对系统的动力学特性有重要影响,预紧力较小时,系统中存在的频率成分较多,有转子的转动频率及其倍频和亚频、支承轴承的变刚度频率及其倍频,系统的非线性较强。随着预紧力的增大,轴承的变刚度频率及其倍频消失,其所对应的幅值减小,系统的非线性特性减弱。应当注意的是,轴承预紧力不可过大,否则将使轴承摩擦加剧,温度升高,影响轴承的使用寿命。因此,在实际使用过程中,应根据情况,对轴承施加合适的预紧力。
2.2.2 径向力的影响
图10是改变径向载荷时转子质心处的振动频率响应。径向载荷较小时,转子质心处的振动频率响应中仅存在转子的转动频率及其倍频和亚频,且其倍频和亚频对应的幅值较小。当径向载荷增大时,转子质心处的振动频率响应中出现轴承的变刚度频率及其倍频,转子转动频率倍频和亚频、轴承变刚度频率及其倍频所对应的幅值也随之增大,加剧了转子系统的振动。
2.2.3 转速的影响
在300 N径向力作用下,不同转速时转子质心的振动频率响应如图11所示。在低速时,系统中的振动频率成分不仅包括转子的转动频率及其亚频和倍频,还有轴承的变刚度频率;随着转速的升高,轴承的变刚度频率消失,系统的非线性特性减弱;转速继续升高,轴承的变刚度频率又重新出现。因此,存在一个最佳转速区间,在此区间内,既可减弱系统的非线性特性,又能降低转子的振动位移。
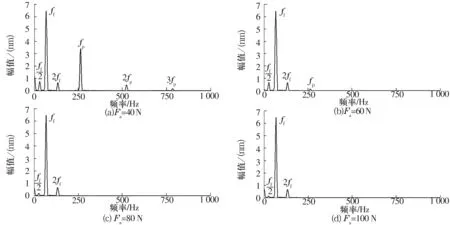
图9 不同预紧力时转子质心的振动频率响应
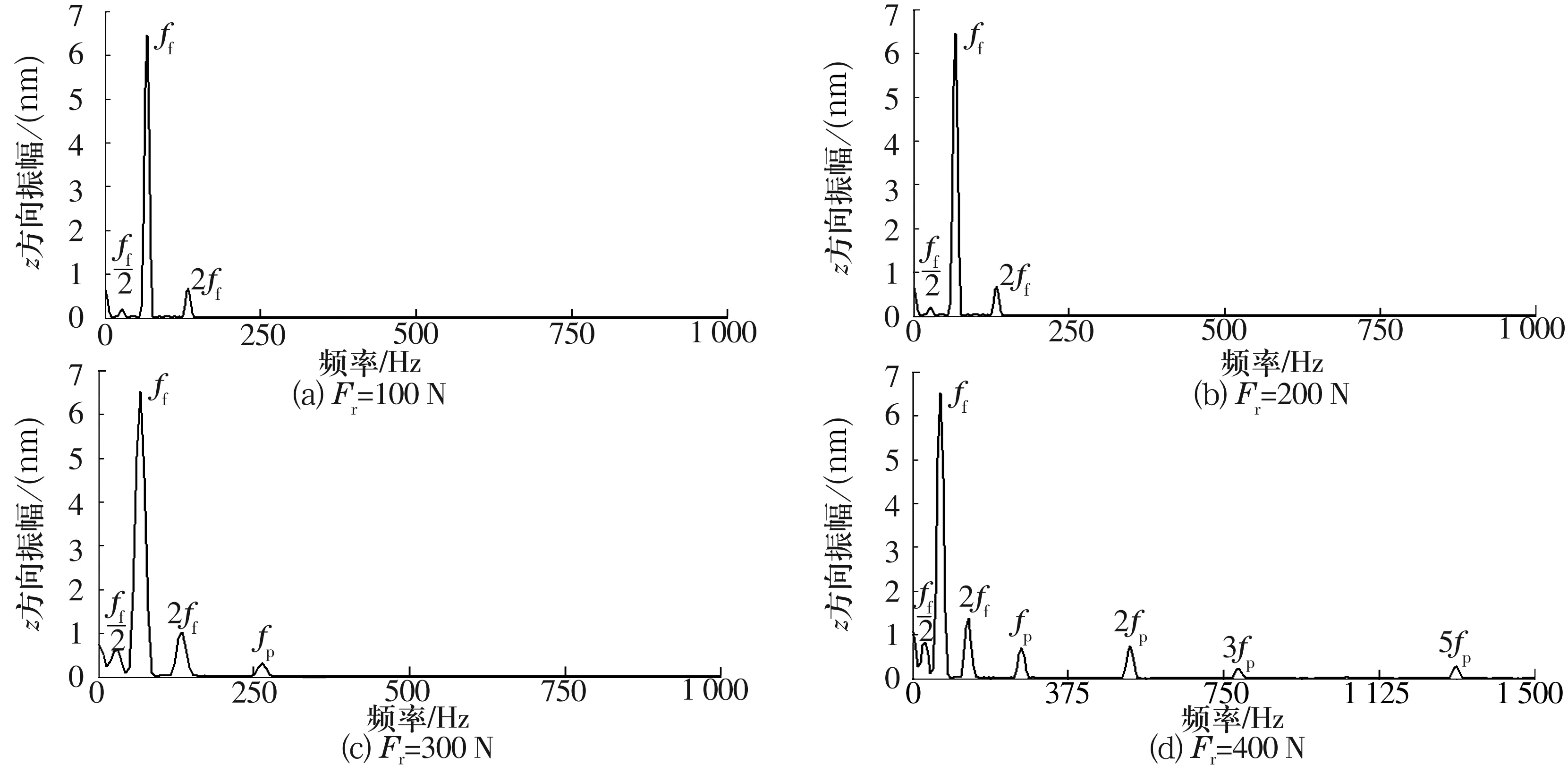
图10 不同径向力时转子质心的振动频率响应
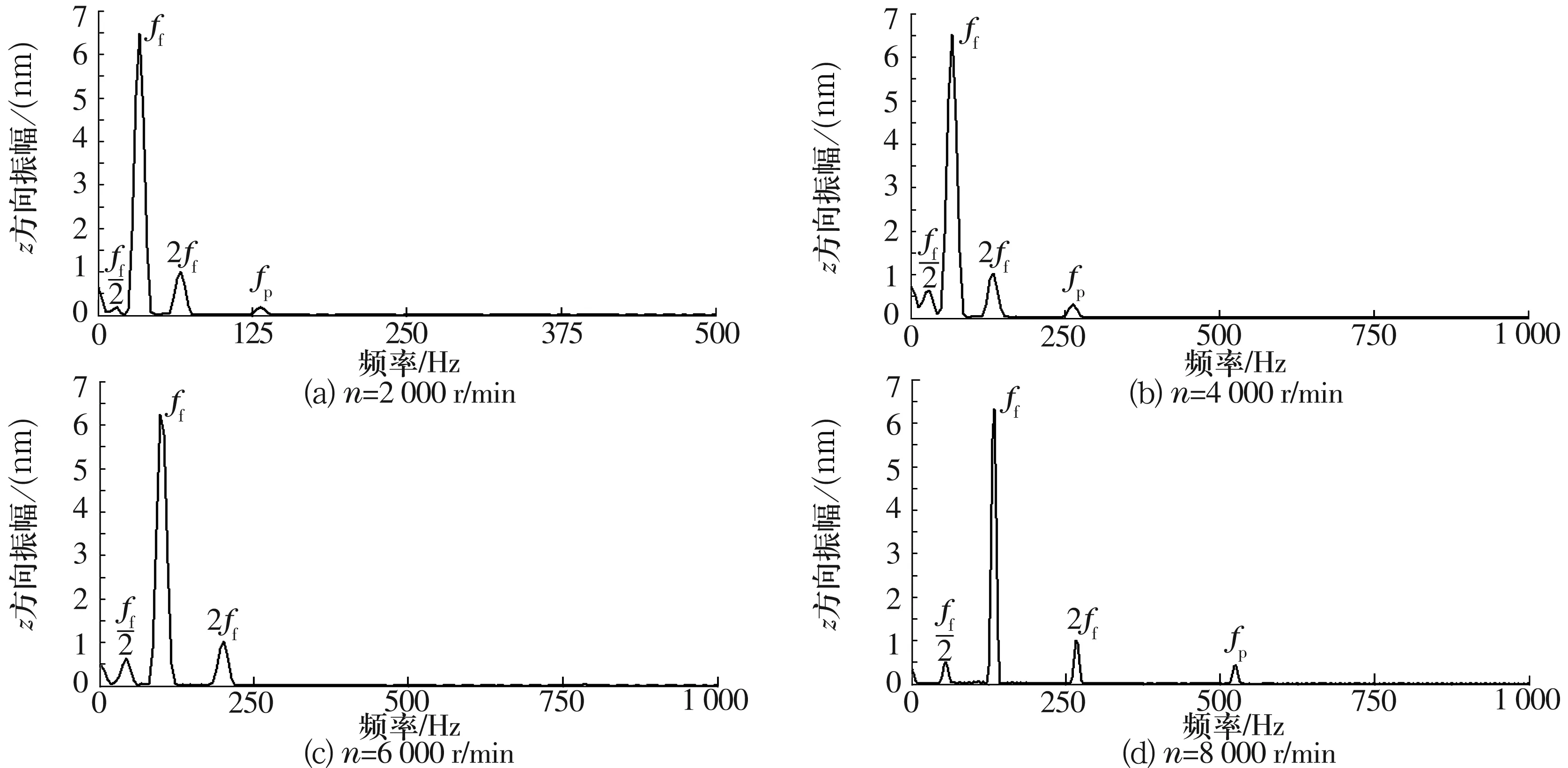
图11 不同转速时转子质心的振动频率响应
3 结论
(1)系统中转子的转动频率始终存在,支承轴承的变刚度频率随着轴承结构参数和系统工况参数的不同而出现或消失。
(2)轴承内、外沟曲率半径系数的变化不改变系统中已存在的振动频率成分。
(3)系统的非线性特性随支承轴承钢球个数、轴向预紧力的增加而减弱,随径向载荷的增大而增强。
(4)存在一个最佳转速区间,在此区间内,系统的非线性特性较弱。

