一种新型趋近率的无刷直流电动机伺服系统变结构控制

刘保连，丁祖军，金德飞

(淮阴工学院，江苏淮安223003)

0 引 言

无刷直流电动机具有体积小、重量轻、维护方便、高效节能以及易于控制等一系列优点而广泛运用于航空航天、工业自动化、医疗器械、计算机外围设备等方面［1］。无刷直流电动机是一种多变量、变参数、强耦合的非线性系统，当系统负载或参数发生变化时，传统控制器控制难以实现对电机进行精确控制。一些研究将极点配置和最优控制、神经网络控制、模型参考自适应控制等引入电机控制技术中，有效提高了无刷直流电动机的运行性能，但这些控制仍依赖于电机精确的数学模型，系统性能易受参数变化及各种扰动的影响，鲁棒性差。

变结构控制作为一种特殊的非线性控制，由于滑动模态对内部参数摄动和外部扰动具有良好的鲁棒性，引起了人们的关注并取得了不少成果。

文献［2］用RBF神经网络为滑模动态补偿器对不确定系统进行控制，系统抗参数摄动、抗干扰性能较好，有效地减弱了单纯滑模变结构控制所带来的“抖振”现象，但算法复杂，难以实现。

文献［3］结合幂次趋近率能够使系统平滑的进入滑动模态的特点，得到一种新型趋近率，提高了传统变结构控制的性能，但滑模到达时间是不确定的。

而单纯的指数趋近律及组合趋近律在滑模面附近减速防抖的性能会因控制器切换功率的不同而参差不齐，到达时间也不是最短。本文提出了一种基于PID趋近率的变结构控制策略，以PID控制规律来控制到达滑模面的速率，其达到滑模面的时间是有限的，且确定的。仿真结果表明本文所提出的变结构控制策略具有较高的动态性能和鲁棒性。

1 无刷直流电动机数学模型

在分析和仿真计算中直接采用相变量法，根据转子位置用分段线性表示感应电动势。由于稀土永磁材料的磁导率很低，转子的磁阻很高，其影响可忽略不计。此时，无刷直流电动机的三相定子电压的平衡方程式可用下列状态方程表达:

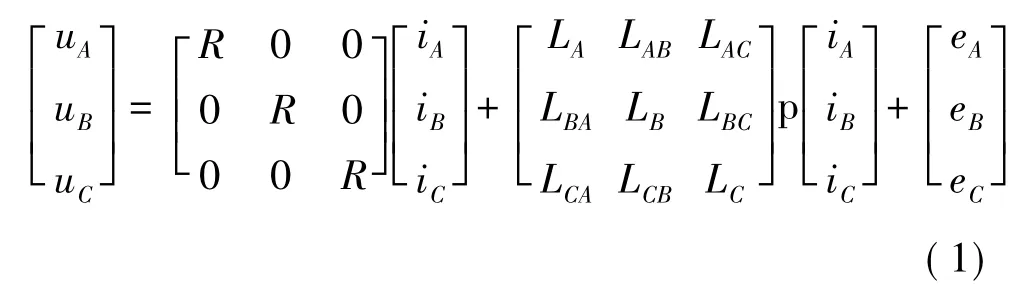
式中:uA、uB、uC为三相定子电压;eA、eB、eC为三相定子反电动势;LAB、LAC、LBA、LBC、LCA、LCB为三相定子间互感;p为微分算子。

由电动机结构决定了在一个360°电角度内(机械上为一对磁极距)，转子的磁阻不随转子位置变化而变化，并假定三相对称，则有:

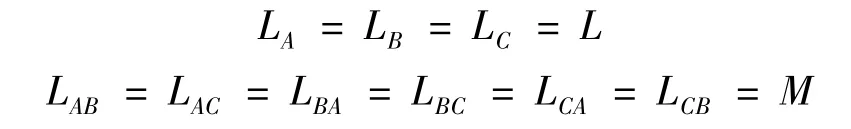
所以式(1)可改写:

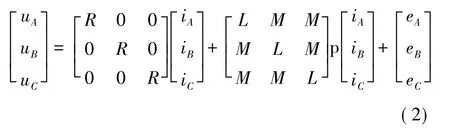
又因为三相对称电机中存在iA+iB+iC=0，所以MiA+MiB+MiC=0，故式(2)整理:

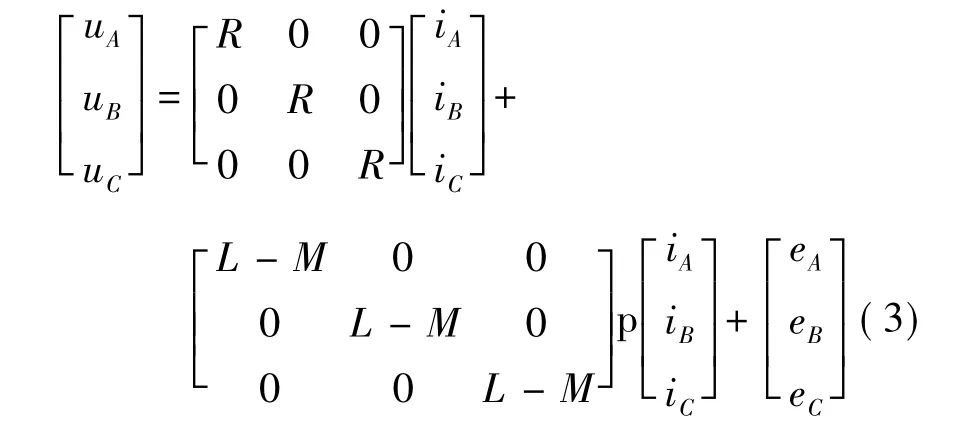
其等效电路如图1所示。

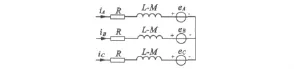
图1 无刷直流电动机等效电路图

电磁转矩方程:

式中:ω为电机转子的角速度。

为了产生恒定的电磁转矩，在每个半周期内，方波电流的持续时间为120°电角度，梯形波反电势的平顶部分要120°电角度以上，两者应严格同步。理想情况下，任何时刻定子绕组只有两相导通，设每相感应电动势为e，则电磁转矩:

式中:e为定子绕组各相反电势;i为定子绕组各相电流。

又因为:

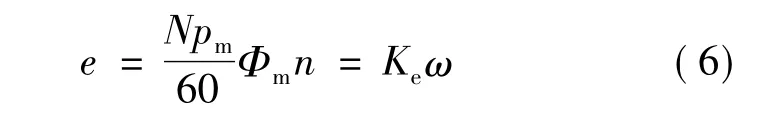
可以看出无刷直流电动机的感应电动势与转速成正比。式(6)代入式(5)，电磁转矩表达式可化为:

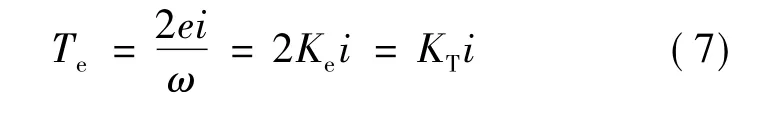
由式(7)可以看出，电磁转矩大小与电流幅值大小成正比，所以控制逆变器输出方波电流的幅值即可控制无刷直流电动机的转矩。

把整个电机当作一个整体，则有:

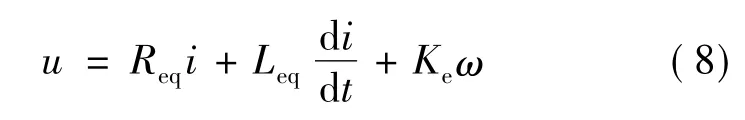
式中:u为电机电压，Req=2R，Leq=2(L－M)。

转子运动方程:

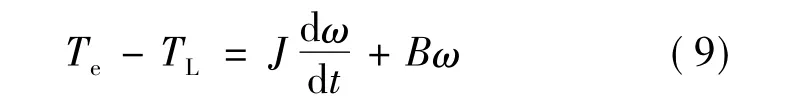
式中:TL为负载转矩;B为粘滞阻尼系数;J为转子及负载的转动惯量。

2 变结构控制器设计

无刷直流电动机伺服系统一般采用电流环、速度环和位置环三环控制结构。速度环用来控制速度，其输出为电机相电流给定值，采用本文所提出的变结构控制器;电流环用来控制电机的电流，提高电机转矩响应性能，防止电机过流;位置环主要是实时采样转子位置信号，为电机换相提供依据，同时可以计算得到电机转速。

无刷直流电动机伺服系统控制原理结构框图如图2所示。

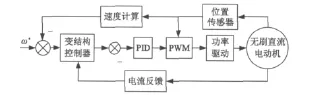
图2 控制原理框图

2.1 PID趋近率设计

变结构控制就是当系统状态穿越状态空间不同连续曲面时，控制器将按一定规律发生变化，使得控制系统对被控对象的内在参数变化和外部扰动具有一定适应能力，从而保证系统性能达到期望指标要求，其实质是一种非线性鲁棒控制。

滑模变结构控制器的设计主要包括两个方面的内容:(1)根据对动态特性的要求，选取合适的滑模面;(2)设计确定的控制率，使滑动运动渐近稳定并具有良好的动态品质。

变结构控制虽然对系统参数及扰动不敏感，具有很强的鲁棒性，但其存在抖振问题，解决这一问题关键在于在到达滑动模态之前所采用的趋近率。本文采用一种PID趋近率来减小变结构控制的抖振及到达滑模面时间。

设滑模面:

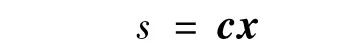
式中:c=［c1，c2，…，cn－1，1］，x=［x1，x2，…，xn］T，为系统状态变量。稳态时我们期望s为0，即s*=0。同一般反馈控制一样，设误差es=s*－s=－s，则滑模面PID趋近率:

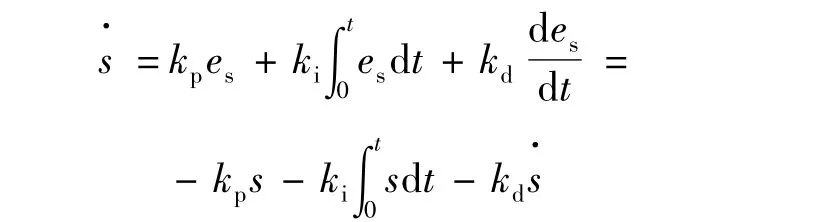
即:

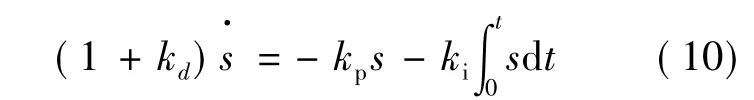
对式(11)两边求导得:

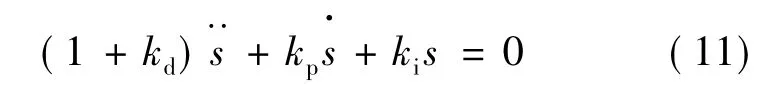
式(11)是一个二阶微分方程，其特征方程:

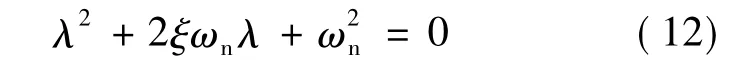
式(12)有一对共轭复根，则式(12)的解:

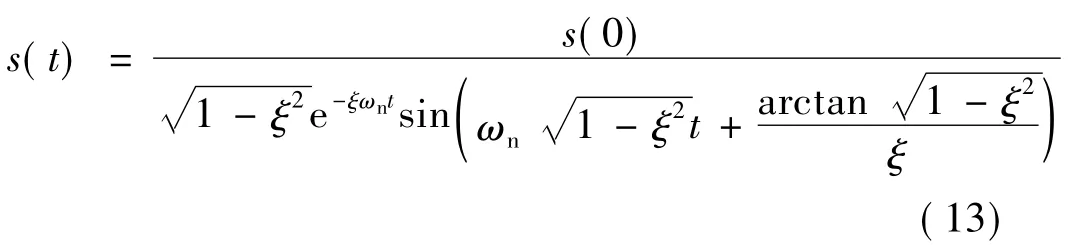
式中:s(0)为初始状态，由式(13)可以看出，系统状态按指数衰减振荡规律趋近滑模面。令式(13)等于0，则可得第一次到达滑模面的时间:

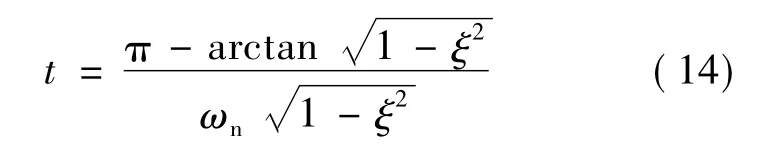
由式(14)可以看出，只要PID参数确定，其到达滑模面的时间也是确定的。

2.2 变结构控制器设计

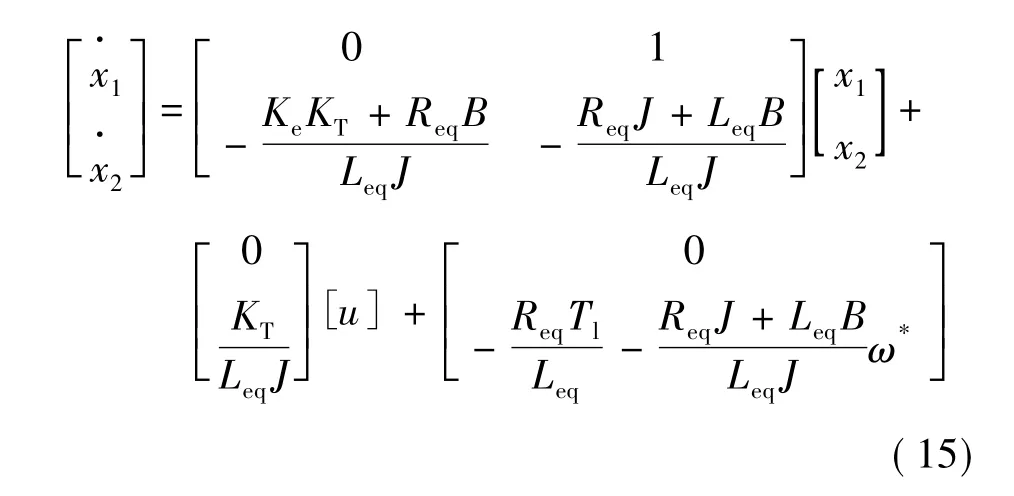
即:

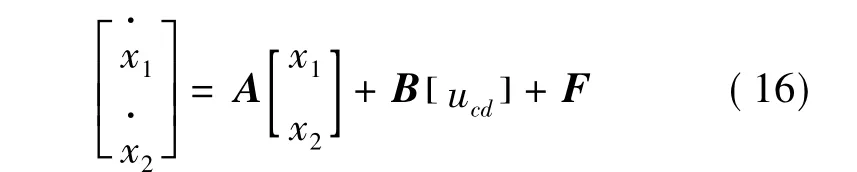
设切换函数:

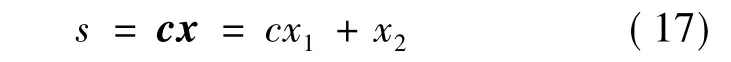
系统为进入滑模面之前，按前面所提出的PID趋近率来设计切换控制量。由式(10)和式(17)可得:

式中:ueq为系统进入滑模面后的等效控制量。

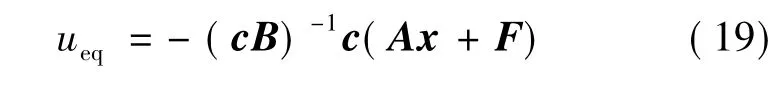
3 仿真及实验结果

为了验证控制策略的可行性及其性能，对系统进行了仿真及实验，图2为在MATLAB/Simulink中搭建了无刷直流电动机伺服控制系统仿真模型。仿真参数:无刷直流电动机额定电压36 V，额定转速nN=3 600 r/min，反电动势系数 Ke=0.065 V·rad·s－1，Leq=1.336 mH，转矩系数 KT=0.071 2 N·m/A，相电阻R=0.35 Ω，忽略粘滞阻尼系数 B。转动惯量 J=1.543 ×10－5kg·m2。PWM 控制策略采用PWM_ON_PWM调制方式。PWM_ON_PWM可以完全消除非换相期间非导通相上的二极管续流现象。与采用传统PWM调制方式相比，在相同的开关频率和开关损耗下，改善电流波形，减小电磁转矩脉动，尤其在中低速区域对总的电磁转矩脉动情况具有明显的改善作用，从而增加电机运行的平稳性［4］。图3～图5给出了仿真波形，图6～图8给出了基于TMS320F2812控制平台的无刷直流电动机伺服系统实验波形。

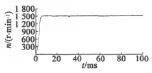
图3 转速响应曲线

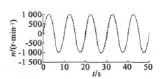
图4 速度跟踪响应曲线

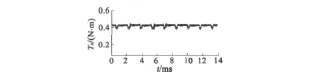
图5 电磁转矩波形

图3给出了转速响应曲线，速度给定1 500 r/min，并且在30 ms时突加扰动负载。由图可以看出，采用本文的变结构速度控制器后，系统响应速度快，基本无超调，转速平稳无静差。突加负载扰动时，系统能够快速跟踪响应，消除扰动对转速的影响。

为验证控制器的跟踪性能，将一正弦波作为速度给定信号，幅值为±1 000 r/min，频率为0.1 Hz，且在20 s时将电枢电阻R突然增大到0.4 Ω。图4给出了跟踪响应曲线，其中实线部分是速度指令，虚线部分是实际跟踪的速度。由跟踪曲线可以看出，系统可以快速而准确地跟踪给定速度，保持相位误差接近零，同时幅值一致;系统参数变化时，系统跟踪性能基本不受影响，跟踪控制精度较高，鲁棒性较强。

图5给出了在速度指令不变的情况下，系统平稳运行时的转矩波形。由图5可以看出，在换相时及不换相期间转矩脉动都很小，保证了转速响应的平稳性。

图6给出了系统运行时电机线电压波形，波形基本呈梯形。图7给出了电机相电流波形，间隔60°呈正负交替矩形波，电流基本平稳，脉动小。无刷电动机换相过程引起电流波形中间有突变，但抖动较小。

系统通过DSP捕获单元捕获无刷直流电动机位置信号，并计算转速，通过控制板卡上的DA转换器输出与转速成正比的电压信号。图8给出了转速信号波形，由图8可以看出，正常运行时，转速平稳，基本无脉动。当突然增加转速给定时，转速跟踪速度快，超调小，整个调节过程大约6 ms，转速再次平稳，这与图3的仿真曲线是一致的。

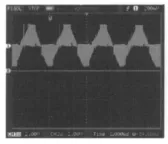
图6 线电压波形

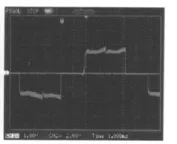
图7 电机相电流波形

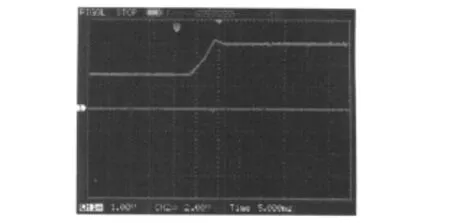
图8 电机转速信号波形

4 结 语

本文根据电路基本定律建立了无刷直流电动机基本数学模型，无刷直流电动机伺服系统参数时变及负载扰动会严重影响系统的动态跟踪性能和鲁棒性。针对这些问题，本文提出了一种PID趋近率的变结构控制策略，使得切换函数到达滑模面的时间是确定的，且该算法简单易于实现。仿真和实验结果表明，系统响应速度快，基本无超调，转速平稳无静差。在突加给定以及存在负载扰动及参数变化时，系统能够快速跟踪响应，消除扰动对转速的影响，跟踪性能基本不受影响，表明了本文所提出的方案是有效的，跟踪控制精度高、鲁棒性强。

［1］ 高宁宇，刘贤兴.滑模变结构的BLDCM直接转矩控制系统研究［J］.微计算机信息，2009，25(2－1):55 －56.

［2］ 安树.基于RBF网络的滑模变结构控制在无刷直流电机伺服系统中的应用［J］.军械工程学院学报，2010，22(2):61 －62.

［3］ 李林杰，焦振宏，时建欣.基于滑模变结构控制的对转无刷直流电机调速系统［J］.微特电机，2010，38(10):44 －47.

［4］ 韦鲲，胡长生，张仲超.一种新的消除无刷直流电机非导通相续流的PWM调制方式［J］.中国电机工程学报，2005，25(7):104－108.

［5］ 瞿少成，王永骥.BLDC位置伺服系统的离散变结构控制［J］.中国电机工程学报，2004，24(6):96 －99.

［6］ 贾洪平，魏海峰.无刷直流电机滑模变结构电流控制［J］.微电机，2010，43(2):58－61.