浅析数值仿真技术辅助《数理方程》教学与研究

◆刘今子 郭立丰 周少华

(东北石油大学数学科学与技术学院)

一、数值仿真技术是《数理方程》教学的新手段

《数理方程》作为理工专业的必修课和重要基础课，因其课程内容抽象，推导繁琐，教师感觉教的费劲，学生普遍很难学懂。MATLAB是用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，在数学类科技应用软件中在数值计算方面首屈一指。

应用MATLAB求解《数理方程》中的问题，节省计算过程的冗繁，还可以把数理方程的解和特殊函数以图形的形式表达出来，给学生以形象、直观的感受，便于理解和教学。最终，把数学的代数、几何和数值三个定量描述完整的展现给学生，加深学生的理解，也利于教师执教，可以取得良好的教学效果。

二、激发教学相长的“互动式”学习模式

1.确定主客体的主次地位。在教学过程中，应坚持以数学物理为主，MATLAB为辅;教学为主，求解为辅;学生为主，教师为辅。因此，无论是课堂演示，还是课下作业，都要针对课堂讲授内容，紧扣数学思想，突出数学求解的核心过程。

2.充分调动学生学习的积极性。通过数值演示的环节，帮助克服学生畏惧困难的心理，并且循循善诱，由浅入深，把传统的用符号及公式表达的定量描述、用几何图形表述的定量描述和用数值表达的定量描述三者结合，抓住学生的学习兴趣，结合数学思想进行教学。

3.突出学习的互动式本质。在课堂教授的同时，提出一些可以“举一反三”的问题，促进学生思考，并自己动手编写程序，进行解决。例如，特殊函数的有关章节，可以训练学生独立动手编程的能力;对于几大典型方程，可以鼓励学生尝试多种求解方法，对学生进行分队，3个人一组，进行团队合作，每人完成一种方法，然后组内进行比较，并递交最终优选方法，进行分析和说明。教师选择比较好的方法进行讲解，这极大地有助于加深学生对《数理方程》的核心求解方法的认识。

4.结合多种思维方法，促进教学效果。课堂讲授结合学生自主学习的同时，教师还可以利用当下流行的思维导图对《数理方程》进行思维分解，逐步引出格林函数方法、变分方法、积分变换方法和差分法等的思维来源，展开头脑风暴，刺激学生的创新思维方式。

三、应用数值仿真技术在数理方程中的典型范例

以有界弦振动问题为例。

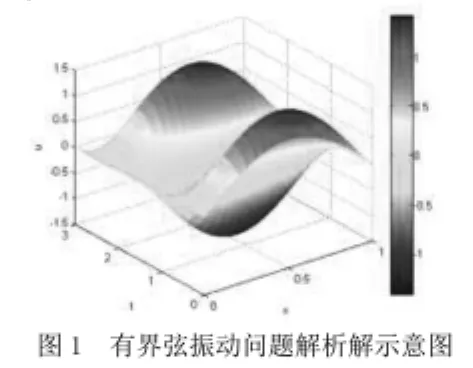
讲解时，注意三角函数的本质特点:“二阶导等于本身或本身的相反数”，这一特殊性质，由此推断出原方程的基矢组必是三角函数组(正弦函数和余弦函数族及其组合)，并通过分离变量方法，详细的叙述傅立叶级数解的求解过程，剖析推导核心思想。

四、结束语

将MATLAB应用于《数理方程》的教学改革中，坚持以数学物理为主，MATLAB为辅;教学为主，求解为辅，学生为主，教师为辅，把数学的代数、几何和数值三个定量描述完整的展现给学生，提出一些可以“举一反三”的问题，促进学生思考和理解，不但锻炼学生的数学思想，强化动手能力，而且利于教师执教，形成“互动式”教学模式，加深学生的理解，加强学生解决实际问题的能力，加快数理方程实用性教改的步伐。

［1］刘卫国.MATLAB程序设计与应用(第二版)［M］.北京:高等教育出版社，2006.

［2］求是科技.MATLAB7.0从入门到精通［M］.北京:人民邮电出版社，2006.

［3］张志涌.精通 MATLAB［M］.北京:北京航天大学出版社，2000.

［4］张元林.积分变换［M］.北京:高等教育出版社，2003.

［5］薛定宇.高等应用数学的MATLAB求解［M］.北京:清华大学出版社，2004.

［6］彭芳麟.数学物理方程的MATLAB解法与可视化［M］.北京:清华大学出版社，2004.