欠驱动航天器姿态调节滑模控制

马广富，刘 刚，黄 静

（哈尔滨工业大学航天学院，150001 哈尔滨）

欠驱动航天器姿态调节滑模控制

马广富，刘 刚，黄 静

（哈尔滨工业大学航天学院，150001 哈尔滨）

针对欠驱动航天器的姿态调节问题，设计了基于滑模变结构控制方法的控制器.给出基于四元数的三轴稳定欠驱动航天器动力学模型和运动学模型，在此基础上首先利用广义逆和二阶滑模趋近律设计了航天器欠驱动轴的姿态调节控制律，给出了欠驱动轴控制器所具有的一般形式，分析了控制器的可实现性，并引入微小摄动量以保证控制器解的存在，在保证欠驱动轴稳定的情况下，又设计了一阶滑模趋近律控制器实现可控轴的调节，最后证明了该控制方法在干扰作用下是有界稳定的，并进行了数值仿真，验证了所推导控制律对欠驱动航天器姿态调节控制的有效性.

姿态调节控制;欠驱动航天器;滑模控制;广义逆

目前所研究的航天器姿态控制系统，一般都安装有足够或冗余的执行机构，正常情况下，航天器姿态控制系统可以在滚动、俯仰和偏航三轴同时输出控制力矩，完成姿态控制，这就是所谓的全驱动航天器姿态控制系统.但在一些特殊情况下，例如某一执行机构发生故障或失效时，在某一方向上无法正常输出力矩，此时姿态控制系统仅能依靠其他两轴输出力矩以维持航天器姿态的稳定，这种情况称为欠驱动航天器姿态控制问题［1］.研究此类欠驱动航天器的姿态控制问题，可以进一步保障系统整体的正常工作，同时提高其可靠性.此外欠驱动航天器以少于标准数目的执行机构实现姿态控制的目的，与其它全驱动航天器相比，具有能耗低、重量轻和成本少等优势.因此，欠驱动航天器的姿态控制问题近年来引起了国内外学者的广泛关注.

由于欠驱动系统不满足 Brockett能稳条件［2］，将其在平衡点附近线性化会导致系统不可控，因此常规的线性控制方法不适于欠驱动航天器的稳定控制问题.在相关的研究中，Crouch［3］首次对所安装执行机构少于常规数目的航天器的可控性问题进行了研究，并设计了相应的控制算法;Morin和Samson［4］设计了指数收敛的时变状态反馈稳定控制器，并通过仿真表明该控制器可以实现欠驱动航天器的姿态稳定控制;Nadjim［5］和ka-zuo［6］等采用Lyapunov直接方法设计了两种不连续的状态反馈姿态稳定控制器.Tsiotras等［7－9］则采用(w，z)参数的描述方式建立了航天器的姿态运动学方程，并设计了多种不连续的姿态稳定控制器;Kim等［10］提出了镇定航天器欠驱动动力学子系统，事先将欠驱动轴角速度控制到零附近后，再设计运动学子系统的滑模姿态控制律以实现局部稳定的控制方法;郑敏捷等［1］同样采用类似的思想，设计反步控制方法实现了对欠驱动轴的有效控制.

近年来，滑模控制方法由于在处理具有动力学模型建模误差等不确定性因素的控制问题时具有较好的鲁棒性，在非线性控制领域吸引了很多学者的目光.Singh 和 Iyer［11］，Dwyer和 Sira －Ramirez［12］，Crassidis［13］分别以不同的姿态描述方式，如欧拉角或Rodrigues参数等设计了多种滑模变结构控制器.Vadali等［14］首先结合最优控制理论设计了一种全局变结构航天器姿态控制器，但在该控制器的设计过程中对模型进行了一定程度的简化，并没有考虑动力学模型中的非线性部分.Terui［15］在其研究基础上考虑了航天器动力学模型中的非线性部分，得到了适用性更广的变结构控制器.Boskovic［16］考虑了控制器输出受限的情况，设计了可在线调节滑模面参数的变结构姿态跟踪控制器.Nusawasrdhana等［17］则在前人基础上更深入研究和探讨了滑模控制器相比于其它一般控制器的优越性.

本文主要考虑了欠驱动航天器的姿态稳定控制问题.首先，应用滑模控制方法的思想对欠驱动轴方向进行调节控制，考虑到欠驱动轴动力学模型的相对阶为2，传统的一阶滑模趋近律无法显式的体现控制力矩与欠驱动轴之间的动力学关系，这里引入了二阶滑模趋近律设计欠驱动轴的控制器，在欠驱动轴达到稳定的基础上进一步实现对其他两轴的有效控制.所设计的控制器将运动学与动力学模型作为1个整体考虑，并且对外部干扰等不确定性因素具有一定的抑制作用，易于工程实现.

1 欠驱动航天器模型建立

本文采用利用四元数描述的刚体航天器运动学和动力学模型，定义航天器本体坐标系相对于惯性坐标系的姿态四元数为

其中q13=［q1q2q3］T为四元数的向量部分，q4为四元数标量部分.为了简化分析，取航天器转动惯量矩阵 J 为对角阵 J=diag(J11，J22，J33)，以滚动轴为欠驱动轴，根据欧拉定理可得到基于四元数的航天器运动学和动力学模型分别为［15］

其中，u=［0 u2u3］T∈R3，ud=［d1d2d3］T∈R3分别为三轴控制力矩与干扰力矩，控制力矩的第1个元素对应欠驱动轴，故恒为零.航天器本体系相对于惯性系的角速度为ω∈R3.

定义a1为

式中a1为航天器的轴不对称系数，表示欠驱动航天器的非轴对称性，其绝对值的大小代表了对欠驱动轴的控制难度，分析可知，a1的绝对值越小，则控制难度越大，a1为零时欠驱动轴将完全无法控制.

2 滑模控制器设计

定义滑动模态向量为

其中k1、k2、k3均为大于零的常数.由于欠驱动轴并不由力矩u作用于该轴的角速度而直接控制，其相对阶为2，所以按照传统的滑模控制设计思路对s求相对于时间的一阶导数无法得到s1与控制力矩u之间的关系表达式，这里对s1求一阶和二阶导数，得

为了保证s1能够渐近收敛至0，取

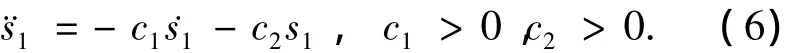
这里式(6)为滑动模态s1的趋近律，类似于传统的二阶系统，通过选择合适的c1、c2可获得不同的趋近效果.将式(4)～(5)代入式(6)可得

所有满足式(7)的控制量ua均可实现对欠驱动轴的控制.下面对ua的可实现性进行分析.

定义1 如果对于任一q∈R4×1、ω ∈R3×1，存在ua满足方程(7)，则称方程(6)通过欠驱动系统(1)、(2)在 q ∈R4×1、ω∈ R3×1可实现.如果任意q≠0、ω≠0均满足上述条件，则称方程(6)是通过欠驱动系统(1)、(2)全局可实现的.

定理1 方程(6)是全局可实现的充要条件为

证明过程详见文献［18］.

根据定理1，很显然当a1≠0时，由式(8)定义的A(q，ω)满足式(11)，所以方程(6)是通过欠驱动系统(1)、(2)全局可实现的.从式(8)还可以看出，欠驱动轴的控制难度与轴不对称系数a1绝对值的大小有关，a1的绝对值越大，控制难度越低.

取控制量ua为

其中A*(q，ω)为A(q，ω)的广义逆，这里定义为

P(q，ω)为控制量系数的零投影矩阵，定义为

其中In×n为n阶单位矩阵，根据Penrose-Moore的定义，式(13)所确定的矩阵A*(q，ω)满足

所以A*(q，ω)满足作为A(q，ω)的广义逆矩阵的条件，并且总是存在且唯一的.

很显然式(12)满足方程(7)，即如式(12)所示的控制器均可保证s1渐近收敛至0.通过选取不同的y可得到方程(7)的所有解.

下面设计y使得系统可以在s2=0、s3=0确定的滑动面上运动.对s2、s3采用舍弃符号函数的指数趋近律

其中，Γ11＞ 0，Γ22＞ 0，

根据式(3)，略去干扰影响，有

将式(12)、(15)代入式(16)可得

由式(14)可知P(q，ω)存在不满秩的情况，即P－1(q，ω)不一定存在，此时根据式(17)无法求得y.这里引入摄动量δ，得到新的控制量系数近似零投影矩阵(q，ω，δ).

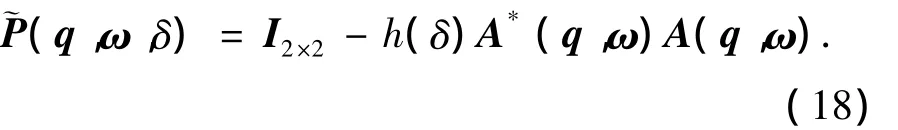
其中 h(δ)=1+ δ.

对A(q，ω)进行奇异值分解，可得

其中 U(q，ω)、N(q，ω)为规范正交矩阵.

根据广义逆的定义式(13)，还可以得到

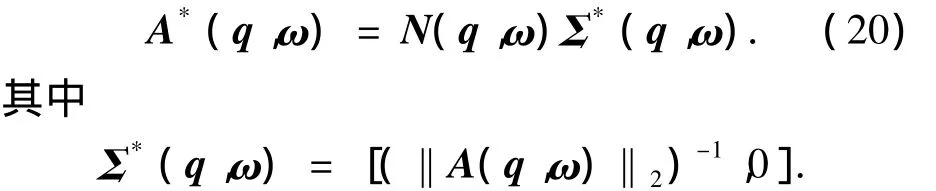
由式(19)和(20)可得

将式(21)代入式(18)中，可得

将式(22)代入式(12)中，得到所设计的滑模控制器为

3 稳定性分析

首先考虑俯仰和偏航两个可控轴的稳定性，选取Lyapunov函数为

不考虑干扰作用时，对其求导可得

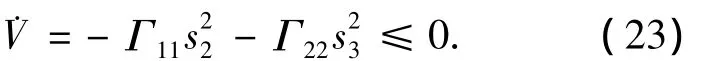
由Lyapunov稳定性定理可以得到以下结论:

由于式(23)当且仅当s2、s3均为零时才满足等于零的条件，所以当系统运动至滑模面上后会一直停留在滑模面上，即沿滑模面运动，系统是渐近稳定的.

考虑干扰的作用，式(23)变为

设干扰是有界的，取一正数η满足0＜η＜1，将式(24)变为

其中|d2|max、|d3|max为干扰幅值的上界.通过观察式(25)发现，只要选取合适的Γ11、Γ22使得

设干扰均是有界的，则式(26)也是有界的.设其绝对值上界为D，将D代入式(6)可得

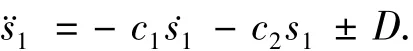
由微分方程的性质可知，D的加入不会改变方程的特征根，设s1的解将由原来的 s1= ηeλat变为 s1= ηeλat±D/c2.其中λa等于λ1或λ2.可以看出只要c2取得足够大，则s1将收敛于零的1个小临域内，从而进一步使q1、ω1收敛至零向量的1个小临域内，所以通过选择合适的c2使系统实现有界稳定.

综上可以看出，在有界干扰作用下，本文所设计的控制器可以实现系统(1)、(2)中所有状态变量的有界稳定.

4 仿真结果与分析

为验证本文所提出的控制算法的有效性，本节在Matlab/Simulink环境下进行数值仿真试验.

航天器转动惯量矩阵为

航天器外干扰力矩为

为了更明显的体现控制器的工作原理和效果，取航天器初始姿态和角速度为

对其进行姿态调节控制，目标姿态和角速度为

控制器参数为 k1=k2=k3=20，c1=4，c2=4，δ=0.001，Γ11= Γ22=0.5.

当采用实际的传感器和执行机构时，受制于执行机构能力和传感器的精度(角速度过大时精度会严重下降)，控制器很难完成上述大角度的调节，这里只是为了定性说明控制算法在理论上的有效性而不考虑角速度和控制力矩过大的情况，该控制器的主要任务还是对外界持续小干扰造成的微小姿态偏差进行调节，防止姿态误差在干扰长时间作用下累积而越来越大.

相应的仿真曲线如图1～7所示，分别为航天器姿态四元数、航天器三轴角速度、控制力矩和滑动模态向量的仿真结果以及稳态误差四元数向量部分放大曲线.

图1 四元数q时间响应曲线

图2 角速度ω时间响应曲线

图3 控制力矩u曲线

从图1～3可以看出，在航天器滚动轴控制输出失效的情况下，本文提出的滑模非线性控制器通过对俯仰和偏航轴的控制仍然可以保证闭环系统的稳定性，在70 s内实现了航天器姿态调节的控制.由于欠驱动轴是通过对其它两轴的直接控制而达到间接控制的作用，所以在稳定过程中可控轴的运动会呈现多次振荡的趋势，振荡程度不仅与控制器有关，还取决于转动惯量矩阵J对角线元素之间的关系.如以a1作为控制难易程度的指标，则a1的绝对值越小，控制难度越高.

图4 滑动模态向量s曲线

图5 误差四元数q1曲线

图6 误差四元数q2曲线

图7 误差四元数q3曲线

通过稳态误差四元数向量部分的曲线可以看出，该控制器对欠驱动轴所施加的持续干扰具有很好的抑制能力，控制误差在1个很小的范围内波动，周期与干扰力矩的周期相同.根据控制器设计的思路，两可控轴需要首先实现对欠驱动轴的控制，而欠驱动轴的控制量是通过两可控轴角速度施加的，所以在对欠驱动轴施加持续干扰的情况下可控轴的控制误差相对较大，波动的频率高于欠驱动轴，其幅值呈现为周期性变化，同欠驱动轴干扰力矩具有相同的频率.该滑模控制器相较于其它的欠驱动控制器，无需将欠驱动航天器运动学和动力学模型分开进行设计，具有较强的通用性.

5 结论

本文针对刚性航天器单轴失效情况下的姿态调节控制问题，利用滑模变结构控制理论，设计了欠驱动刚性航天器姿态滑模控制系统.首先考虑到欠驱动轴相对阶为2的情况，设计基于二阶滑模趋近律控制器对其进行姿态调节.在此基础上，设计传统一阶滑模控制器实现另外两轴的控制.为了保证整个系统的可实现性，引入微小摄动量，得到了完整的滑模控制器.最后采用数学仿真验证了所设计控制器的有效性.

［1］郑敏捷，徐世杰.欠驱动航天器姿态控制系统的退步控制设计方法［J］.宇航学报，2006，27(5):947－951.

［2］BROCKETT R W.Asymptotic stability and feedback stabilization［M］.Boston:［s.n.］，1983:181 －191.

［3］CROUCH P E.Spacecraft attitude control and stabilization:Applications of geometric control theory to rigid body models［J］.IEEE Trans on Automatic Control，1984，29(4):321－331.

［4］MORIN P，SAMSON C.Time-varying exponential stabilization of a rigid spacecraft with two control torques［J］.IEEE Trans on Automatic Control，1997，42(4):528－534.

［5］NADJIM M H，STEPHEN H.Attitude stabilization of an underactuated satellite using two wheels［C］//Proc of the 2003 IEEE Conf on Aerospace.Piscataway:IEEE Press，2003:2629 －2635.

［6］KAZUO TAKATERU U.Attitude control of a spacecraft with two reaction wheels［J］.Journal of Vibration and Control，2004，10(13):1291 －1311.

［7］TSIOTRAS P，CORLESS M，LONGUSKI J M.A novel approach to the attitude control of axis symmetric spacecraft［J］.Automatica，1995，31(8):1099 －1112.

［8］TSIOTRAS P，LUO J.Control of underactuated spacecraft with bounded inputs［J］.Automatica，2000，36(8):1153－1169.

［9］TSIOTRAS P，DOUMTCHENKO V.Control of spacecraft subject to actuator failures:state-of-the-art and open problems［J］.Journal of the Astronautical Sciences，2000，48(2):337－358.

［10］KIM S，KIM Y.Sliding mode stabilizing control law of underactuated spacecraft［C］//AIAA Guidance，Navigation and Control Conf and Exhibit.Boston:AIAA Press，2000:125.

［11］SINGH S A，IYER A.Nonlinear decoupling sliding mode control and attitude control of spacecraft［J］.IEEE Transitions on Aerospace and Electronic Systems，1989，25(5):621－633.

［12］DWYER T A W，SIRA-RAMIREZ H.Variable-structure control of spacecraft attitude maneuvers［J］.Journal of Guidance，Control，and Dynamics，1988，11(3):262－270.

［13］CRASSIDIS J L.Sliding mode control using modified rodrigues rarameters［J］.Journal of Guidance，Control，and Dynamics，1995，19(6):1381－1383.

［14］VADALI S R.Variable-structure control of spacecraft large-angle maneuvers［J］.Journal of Guidance，Control，and Dynamics，1986，9(2):235 －239.

［15］TERUI F.Position and attitude control of a spacecraft by sliding mode control［C］//Proceedings of the American Control Conference，American Automatic Control Council.Evanston，IL:［s.n.］，1998:217 －221.

［16］BOSKOVIC J D，LI S M，MEHRA R K.Robust tracking control design for spacecraft under control Input saturation［J］.Journal of Guidance，Control，and Dynamics，2004，27(4):627 －633.

［17］NUSAWARDHANA，AK S，CROSSLEY W.Nonlinear synergetic optimal control［J］.Journal of Guidance，Control，and Dynamics，2007，30(4):1134 －1147.

［18］BAJODAH A H.Asymptotic perturbed feedback linearization of underactuated Euler＇s dynamics［J］.International Journal of Control，2009，82(10):1856 －1869.

Sliding mode control for attitude regulation of underactuated spacecraft

MA Guang-fu，LIU Gang，HUANG Jing

(School of Astronautics，Harbin Institute of Technology，150001 Harbin，China)

The problem of attitude regulation control of an underactuated spacecraft is resolved by using sliding mode method.The three-axis underactuated spacecraft attitude dynamics and kinematics models are introduced.A sliding mode controller using generalized inverse and second order approaching law is designed for underactuated axis stabilization control，and the realisability of the controller is analyzed.A perturbed null-projection is constructed to guarantee the feasibility of the controller.On the basis of stabilization of the underactuated axis，a sliding mode controller is designed for another two axes as well.The proof of bounded stability is given in Lyapunov＇s sense.Simulation results demonstrate the availability of the proposed control algorithm.

attitude regulation control;underactuated spacecraft;sliding mode control;generalized inverse

V448.2

A

0367－6234(2012)09－0001－06

2011－09－01.

国家自然科学基金资助项目(61004072);中央高校基本科研业务费专项基金资助项目(HIT.KLOF.2010016);

马广富(1964—)，男，教授，博士生导师.

马广富，magf@hit.edu.cn.

(编辑 张 宏)