小卫星PD姿态控制器IP核的FPGA实现
丁玉叶,兰盛昌,华 伊,李梦立,潘 瑞,徐国栋,
(1.哈尔滨工业大学电子与信息工程学院,150001 哈尔滨;2.哈尔滨工业大学 航天学院,150080 哈尔滨)
小卫星PD姿态控制器IP核的FPGA实现
丁玉叶1,兰盛昌2,华 伊1,李梦立2,潘 瑞1,徐国栋1,2
(1.哈尔滨工业大学电子与信息工程学院,150001 哈尔滨;2.哈尔滨工业大学 航天学院,150080 哈尔滨)
针对现代小卫星在姿态控制系统中对运算速度、控制精度等方面提出的更高要求,分析了利用FPGA来实现卫星姿态PD控制器的可行性,提出用输入使能端及输出标志符号对内部各计算模块进行控制以解决数据同步问题.利用硬件描述语言进行了各模块功能的实现,并最终例化为PD控制器IP核.结果表明该设计只需34个时钟脉冲即可完成姿态控制力矩的计算,控制精度达到10-5量级,速度及精度满足现代小卫星对控制系统的要求.
卫星姿态控制;FPGA;IP核;PD控制律
卫星姿态控制系统是在轨卫星保持特定姿态完成特定功能的重要保障,因此对卫星姿态控制器输出力矩的计算速度及精度有着较高的要求.
然而小卫星在轨运行时,需要处理的数据多、任务复杂,加之中断频繁发生,使得单靠传统处理器对姿态进行控制时,控制周期受到较大限制,性能难以大幅度提高.现代小卫星体积小、重量轻、功耗低[1],如何在有限的资源及重量等方面的要求下设计出结构简单、计算速度快及可靠性高的姿态控制系统成为难点问题.利用FPGA可重构的特点及并行运算的优势解决航天问题成为研究的热点[2-4].目前,国内外已有多颗卫星成功将FPGA用于航天领域,包括澳大利亚2002年12月发射的FedSat-1卫星以及Stuttgart大学实施的一项叫做Stuttgart Small Satellite Program的小卫星计划中的第一颗小卫星Flying Laptop,这项计划主要是对未来小卫星的新技术验证.基于FPGA的星载计算机便是其中的一项创新技术[5].将FPGA应用于卫星姿态控制系统也得到了国内外航天领域的重视,相关工作已展开.文献[6-7]都对该问题进行了探讨,并取得了一定成果,但是两者接口选取的数据形式为定点数,与外部系统不宜转换,并且在计算精度方面不能满足要求,计算速度较慢.
为了更好的解决上述问题,本文所设计的小卫星PD姿态控制器IP核采用输入使能信号与输出标志符号进行内部计算控制,解决了数据不同步问题,避免了模块间数据延迟造成的处理速度的降低,可以快速计算出输出力矩,满足速度及精度要求.该IP直接采用32浮点数数据形式进行计算,精度高,同时外部计算机系统的单精度或双精度转换为浮点数较为容易.
1 姿态控制器的设计
目前,卫星上实际应用的姿态控制技术主要为PID或改进PID控制,此外最优控制方法、变结构控制方法、鲁棒控制方法、自适应控制方法、智能控制等先进控制方法等也逐渐被应用[8-9].PID控制中微分信号的引入可提高系统的通频带,加速系统的响应速度,加速消除误差,积分信号可以提高稳定精度,但会出现积分饱和现象,影响控制效果;变结构控制适合非线性系统控制,可靠性强,但是易抖动,影响姿态控制的精度;鲁棒控制适用于将稳定性和可靠性作为首选的系统,但由于一般不工作在最优状态,因此稳态精度差;全系数自适应控制方法以其控制品质好、适应性强和鲁棒性强等优点,已在实际工业控制中取得了成功的应用,但采用FPGA实现控制方法较为复杂;智能控制从提出以来已解决了一些传统控制技术难以解决的问题,而且大大提高了控制性能,受到了人们的极大关注,但缺乏经典控制和现代控制理论那些严格的理论体系和设计方法.PD控制定律形式简洁,适合硬件编程实现快速控制,稳定精度高,因此本文涉及的卫星姿态控制器主要是对常用的PD控制律利用VHDL进行设计.主要包括PD控制律的数学模型及接口设计,模块划分及设计.
1.1 PD控制律数学模型及接口设计
采用欧拉角反馈的PD控制律可以表示如式(1)所示:

其中:kp、kd为比例常数;φc、θc、ψc为3 个控制通道的标准角度;φ、θ、ψ 为3个通道的实时角度;ωx、ωy、ωz为3 个通道的实时角速度,Tcx、Tcy、Tcz为 3个输出力矩.
由上式可见PD控制律完成的是1个计算功能,因此需要综合考虑计算速度、精度及数据转换难易选取合理的数据形式.IEEE标准754有基本的单精度格式浮点数[10],但是由于规格化尾数在小数点前有隐藏的1,进行计算需要先将其移出,计算麻烦且浪费资源,同时单精度格式阶码表数在1~254(偏移127),在进行阶码计算操作时需要考虑偏移,增加运算所需时钟周期数,因此在基本单精度格式上自定义一种32位浮点数,该浮点数表示精度高、计算过程明确,并且进行单精度或双精度浮点数与32位浮点数转换非常容易,因此设计中数据均表示为32位浮点数.
32位浮点数的基本格式如图1所示.

图1 32位点数的基本格式
图中S表示符号位,0代表正数,1代表负数;E[30∶23]代表阶码,为指数项;F[22∶0]代表尾码.
阶码采用移码表示,尾码采用无符号二进制数原码表示.
数字‘0'的意思是只要尾码 F[22∶0]全为 0,则表示该浮点数大小为‘0'.其表示的实际数值为
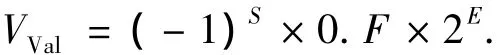
32位浮点数在作加、减法运算时,小数点必须是对齐的,所以阶码不相等的两个浮点数不能直接进行加、减运算.浮点数加减运算的步骤如下:
1)对阶.通过比较阶码大小选择较大者作为结果阶码,同时通过两者差值移动阶码较小数的尾码,使两个操作数小数点对齐.
2)尾码求和.将对阶后的两个尾数按照定点数的运算规则求和、差.
3)规格化.保证尾码的第1个有效数字是1.
4)舍入.精度要求较高时考虑.
5)溢出判断.主要表现为阶码的溢出,由于阶码最大为127,此时表示的十进制数字很大,因此可以不考虑溢出.
两个浮点数相乘,其乘积的阶码是两个数的阶码之和,尾码是两个操作数尾码之积.所以浮点数的乘法运算也要经过如下5个步骤:
1)阶码相加.求出结果的阶码.
2)尾码相乘.求出结果的尾码.
3)规格化.由于尾码相乘结果尾数较多,需要通过规格化选择23位作为结果的尾码,同时移动阶码.
4)舍入.精度要求较高时考虑.
5)溢出判断.主要表现为阶码的溢出,由于阶码最大为127,此时表示的十进制数字很大,因此可以不考虑溢出.
1.2 PD控制律的计算流程及控制设计
由于控制定律在3个方向具有相同的数学形式,因此在FPGA层次化设计中可以只设计其中1个方向,通过顶层模块的三次并行调用完成3个方向的控制功能.
由控制定律的形式可见,整个运算过程中涉及到两次加减法运算和两次乘法运算,因此中间模块包括加法器模块及乘法器模块,如图2所示.利用元件例化语句通过顶层模块按顺序依次调用加法模块和乘法模块可以完成输出力矩的计算[11].由于选取的数据形式为32位浮点数,而浮点数的加法及乘法是按照特定的步骤完成的,因此最底层模块可以按照加、乘法的运算步骤共划分7个模块.层次划分、模块划分及各模块完成功能如图2所示.

图2 层次划分、模块划分及各模块完成功能
由图2可知通过输入端口输入数据会传递给中间加法器及乘法器模块,中间加法器及乘法器模块会分别将该数据按照流程图2、3顺序或并行的传递给底层模块进行各步骤的计算,底层模块会将最终的输出结果返回给顶层模块,并最终输出.整个计算过程中各个模块设置3个输入使能信号及1个输出控制信号,其中1个输入使能端接全局复位信号,另外两个接前面模块的输出控制信号(当前面只有1个模块时,两个使能端均接该模块),上一个(多个)模块或顶层的模块的输出控制信号接下一个(多个)模块或底层模块的使能端,当各模块完成功能后将输出控制信号置高电平(及下一模块使能端置高电平),当所有使能端都为高电平时,模块才允许计算,这样可以保证各模块间的顺序或并行运算,解决了中间计算数据不同步的问题.
1.3 仿真验证
根据上面定律的数学形式、选取的数据形式以及流程和模块划分利用VHDL进行编程,所有底层模块采用进程并行语句时钟触发,首先判断使能端是否为高电平以决定是否启动该模块,其次判断时钟是否为高电平,为高电平时进行本模块计算,保证时序同步;各同级模块之间通过端口映射级联;上下级模块间通过元件例化进行调用,各模块编程设计所用时间如表1所示.

表1 底层模块设计及所用时间
加法器各模块顺序运算,所以完成一次加法需要4时钟周期;由于乘法器的阶码加与尾码乘并行运算,所以这两个模块所用时间为24时钟周期,因此完成一次乘法需要25时钟周期;由图2(a)知,在最后一次加法完成前,存在并行运算,因此之前3次计算所用时间为一次加法及一次乘法所用时间即29时钟周期,所以整个计算过程需要34时钟周期.
仿真结果如图3所示(时钟周期1 μs).由仿真结果可以看出,在第34个时钟周期到来时完成整个计算得出输出力矩.满足卫星姿态快速控制要求.
综合后得到RTL图如图4所示:RTL图表明各模块间运算关系、顶层与底层模块的接口连接符合设计的要求,形成了模块化的PD控制器.

图3 PD控制律仿真结果

图4 综合所得模块级联RTL视图
2 仿真验证及结果分析
由仿真图2可知完成计算共需34个时钟周期,计算速度快,满足卫星姿态控制器对时间的要求,但是手动输入角度及角速度效率低,并且不能输入连续的角度及角速度,导致无法全面的对该IP核计算准确度进行验证,另外需要考虑实时性问题.因此需要进行联合仿真和实时仿真对所设计IP核的稳定精度及实时计算速度进行验证.
2.1 联合仿真系统模型
利用Matlab的M文件编写的S-function和Simulink模块建立微小卫星姿态控制仿真系统,其总体框架如图5所示.该仿真系统主要包括卫星运动学模块,卫星动力学模块,PD控制定律模块.其中PD控制模块内部包括输入输出转换模块.PD控制定律模块链接到Modelsim中具体的HDL实体.
将Matlab与Modelsim连接时,Matlab作为服务器,而Modelsim作为客户端,Matlab对Modelsim仿真器发出的服务请求做出响应,建立通信连接,并调用1个具体的封装函数对在Modelsim下仿真的HDL模型进行数值计算和验证分析[12].

图5 联合仿真模型
由于外部模型数据均采用IEEE标准754中基本双精度浮点数,因此需要进行数制转换.首先需要将基本双精度与基本单精度浮点数进行转换,利用强制转换函数将基本双精度浮点数与基本单精度浮点数转换.再利用C语言编写转换函数,将基本单精度浮点数与32位浮点数进行转换.转换流程如图6.
2.2 联合仿真端口设置
联合仿真模块的参数对话框包括输入输出端口设置、时钟周期及触发方式设置、Simulink与Modelsim仿真时间的对应关系、Simulink与Modelsim的连接方式,以及仿真前后执行的TCL命令5个部分,其中连接方式采用 TCP/IP套接字(TCP/IP socket)方式,TCL命令可以不设置.本硬件姿控仿真模块其他具体参数设置如表2~4所示.
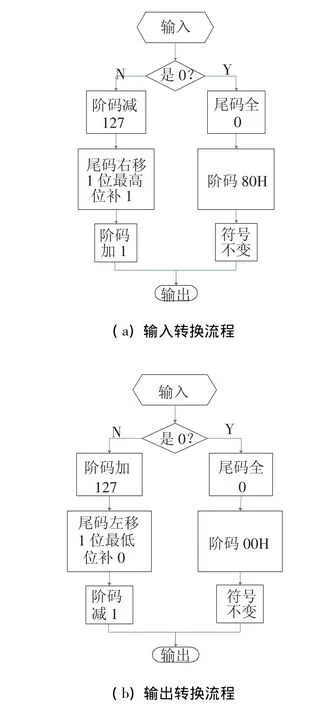
图6 输入、输出转换流程

表2 联合仿真输入输出端口设置

表3 联合仿真时钟设置

表4 联合仿真时间对应设置
2.3 联合仿真结果及分析
建立如表5所示的实时仿真参数,仿真后所得结果如图7所示.

表5 PD控制实时仿真参数

图7 三个通道控制角度仿真
可见,3个方向的姿态角度都是从0°开始,在经过50次计算后使控制角度接近于0.3°,在经过100次计算后使卫星姿态角度达到基本等于0.3°,误差如图 8.

图8 3个通道的误差
由图8可知达到稳定后实时角度与控制标准角度的绝对误差远低于10-5数量级,能够满足中高精度指向卫星的姿控要求.说明本文设计的姿控算法的FPGA实现可以在精度方面满足卫星对姿态控制的需要.
2.4 实时仿真验证
前面利用Matlab与Modelsim进行了联合仿真验证,得到较好的结果,但以上仿真均是非实时性的仿真,与实际系统的工作有一定的差别.建立基于PC/104和FPGA的实时系统仿真平台,可以很好的检验该设计的实用性.
利用CAN总线将xPC实时仿真机和基于FPGA的嵌入式处理器连接起来.并将PC机接入CAN总线,用于监视CAN总线上的数据.在PC机上利用Matlab/Simulink将卫星姿态动力学、姿态运动学模型转换成RTW代码,下载到实时仿真机中;同时在PC机上利用Xilinx FPGA EDK软件,将PD算法IP核添加到MicroBlaze嵌入式处理器中,生成姿态控制器,下载到 FPGA开发板中,进行实时仿真验证.利用CAN总线向处理器发送姿态参数,处理器调用 PD控制器进行100 000次计算,之后将结果返回给CAN总线,通过时间差可以求得实时计算所需时间,计算时间测试结果如表6所示.

表6 实时仿真计算时间
通过基于PC/104和FPGA之间的实时系统仿真可以看出实时仿真计算时间较短,说明使用FPGA进行计算速度较快.说明本文设计的姿控算法的FPGA实现可以提高计算速度以满足卫星对姿态控制的需要.
3 结论
卫星姿态控制器快速精确的进行输出力矩计算是姿态控制的关键,而利用FPGA并行运算的特点来实现卫星姿态控制定律,通过设计输入使能信号及输出标志符号解决数据同步问题,能够大大缩短运算时间,满足了高精度观测等姿态控制系统高响应速度的要求,并且所选32位浮点数精度高,计算舍入误差小,大大提高了输出力矩的计算精度.此外采用模块化实现的PD控制律IP方法可以重复利用,大大缩短了研发周期,减少了成本,有效地满足了航天器对时间成本及质量的要求.
[1]JILLA C D,MILLERR D W.Satellite design:past,present and future[J].International Journal of Small Satellite Engineering,1997,1(1):234 -240.
[2]SALCIC Z,LEE C R.FPGA-based adaptive tracking estimation computer[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):699 -706.
[3]DEUTSCHMANN J,BAR-ITZHACK I Y.Extented Kalman filter for the ocean topography experiment satellite[C]//Flight Mechanics and Estimation Theory Symposium.Washingtong,DC:NASA,1989:333-345.
[4]SHUSTER M D.Efficient estimation of attitude sensor coalignments[C]//Proceedings of the AIAA/AAS Astrodynamics Conference.Washington,DC:AIAA,1994:45-53.
[5]武文权.可重构并行小卫星星载计算机体系结构设计[D].上海:中国科学院研究生院,2004:1-9.
[6]谢祥华.微小卫星姿态控制系统研究[D].南京:南京航空航天大学,2007:64-87.
[7]戴彦.基于FPGA的卫星姿态控制系统的设计与仿真[D].哈尔滨:哈尔滨工业大学,2007:42-50.
[8]WEI X,GUO L.Composite disturbance-observer-based control and H∞control for complex continuous models[J].Int J Robust Nonlinear Control,2010,20(1):106 -118.
[9]BOLONKIN A A,KHOT N S.Optimal bounded control design for vibration suppression[J].Acta Astronaut,1996,38(10):803 -813.
[10]覃霖,曾超.基于VHDL实现单精度浮点数的加/减法运算[J].电子工程师,2008,34(7):52 -53.
[11]詹仙宁.VHDL开发精解与实例剖析[M].北京:电子工业出版社,2009:9.
[12]范静,陈文艺.基于Modelsim与Matlab/Simulink联合仿真技术的接口与应用研究[J].西安邮电学院学报,2010,15(3):73 -74.
The FPGA implementation of IP core of PD attitude controller for small satellites
DING Yu-ye1,LAN Sheng-chang2,HUA Yi1,LI Meng-li2,PAN Rui1,XU Guo-dong1,2
(1 School of Electronic And Information Engineering,Harbin Institute of Technology,150001 Harbin,China;2.School of Aerospace,Harbin Institute of Technology,150080 Harbin,China)
In the sight of the higher requirement about operation speed and control accuracy in satellite attitude control system,this paper analyzed the feasibility of PD attitude controller by using FPGA,and proposed a method using the input enable and the output control symbol to dominate the internal calculation module to figure out the problem of data synchronization.The paper used hardware description language to achieve the function of each module,and finally instantiated the IP core of PD controller.The result shows that the design is able to accomplish the calculation of attitude control torque by only using 34 clock pulses and the accuracy of control can reach 10-5magnitude.The speed and accuracy meet the needs of the modern small satellite control system and lay the foundation for using FPGA implementation in small satellite attitude control system.
satellite attitude control;FPGA;core of IP;control law of PD
TP3332
A
0367-6234(2012)09-0040-06
2011-09-15.
国家自然科学基金资助项目(60904051);中国博士后科学基金资助项目(20090450126);微小型航天器技术国防重点实验室开放基金资助项目(HIT.KLOF2009091).
丁玉叶(1988—),男,博士研究生;
徐国栋(1961—),男,教授,博士生导师.
丁玉叶,dyytianzhijiaozi@gmail.com.
(编辑 张 宏)

