漫谈一堂好课的基本特点

顾 琦

（无锡市第一中学，江苏 无锡 214000）

近日，笔者随堂听了江苏省某教授级高级教师的一节物理新授课“匀变速直线运动的位移与时间关系”，回顾整堂课的教学活动过程，十分值得好好品味消化.同时，笔者又回想起工作以来听过的其他优秀案例，发现这些优秀教师的课堂教学都具有一些共性.

1 “干净”的教学过程

首先，教师的教学思路是“干净”的.这才能让学生轻松地抓住课堂的主线.这节课的流程如图1所示：先简短回顾了匀速直线运动的位移公式、x－t图线，并利用v－t图线轻而易举的解决了匀速直线运动v－t图线中速度v与面积S的对应关系；接着又回顾了匀变速直线运动平均速度的公式和速度公式，又对匀变速直线运动的x－t图线做了简单介绍，并重点讨论了匀变速直线运动的v－t图线；然后，利用得到的v－t图线中位移x与面积S的对应关系，从几何面积的角度导出了位移随时间变化的计算式，甚至包括平均速度的计算式、速度与位移的计算式；最后通过对几个常用计算式的比较，分析各个计算式的特点并通过实例强化学生对计算公式的选择.

其次，教师的语言是“干净”的.简洁、直达要点的语言能让学生快速找到重点，不会无谓地浪费学习中的兴奋点.在该堂课中，学习内容的引出和过渡简洁而自然，比如在课堂刚开始准备研究匀速直线运动的相关知识时，教师是这样表述的：“我们最熟悉的运动是匀速直线运动”，而当课堂内容过渡到匀变速直线运动的相关知识讨论时，教师又是这样过渡的：“我们最近最关心的运动是匀变速直线运动”；而对于教学中涉及的非本次教学主干知识的内容，言简意赅地带过，又给以后学生的学习留有空间，比如在讨论匀变速直线运动的x－t图线时，该教师是这样表述的：“匀变速直线运动的x－t图线比较复杂，以后大家会知道它就是同学们在初中数学中学习过的抛物线，其中速度v的大小仍然可以用曲线上某点切线的斜率tanα来表示，这个问题我们以后再详细讲.”作为与匀速直线运动的对比教学，刻意回避匀变速直线运动的x－t图线会显得很勉强，而过多的深入讨论又会带偏课堂教学的重点，如此简单带过的处理方法既将一块完整的知识处理得滴水不漏，又留有学生自己思考的余地.

“干净”的课堂就好像电影中干净的画面，重点突出，听这样的课让人思路清晰，目的明确.

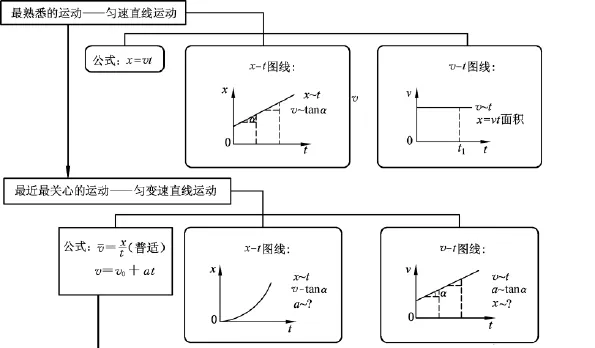
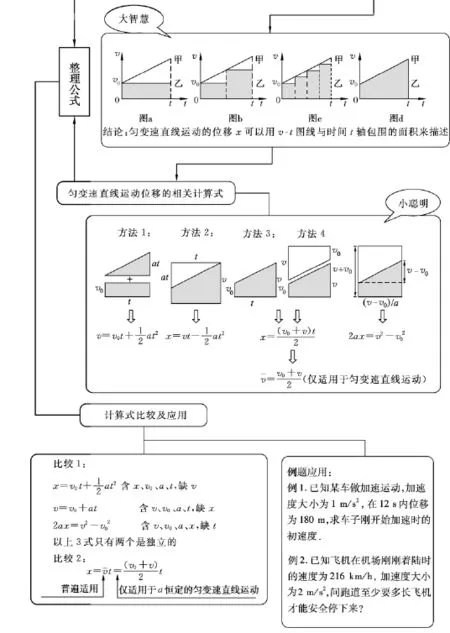
图1

2 化繁为简的教学策略

一位好的教师懂得如何把教学中出现的难点处理得深入浅出.

“化繁为简”，可以借助学生熟悉的东西，拉近学生与未知知识间的距离.在上文中提到，匀变速直线运动x－t图线的表述中，该教师“刻意”而“不经意”地用到了“它就是同学们在初中数学中学习过的抛物线”，这样的措辞让学生与完全未知的知识间产生了“可以亲近”的联系，即使不进行深入的讲解也不会让学生产生盲目的神秘感，同时也给学生课后自己思考指出了方向.

“化繁为简”，可以采用比较的手法，特别是实例比较的方法提高学生的感性认识.本节课最大的教学难点就是如何让学生理解匀变速直线运动的v－t图线和匀速直线运动的v－t图线一样，位移x可以用图线和时间轴包围的面积来表示.该教师在课堂上是这样处理的：

师：有一辆车，甲车做初速度为v0的匀变速直线运动，另有一辆乙车做速度为v0的匀速直线运动，两者的图线如图2（a）.在t时间里，乙车的位移在图中如何表示？

生：（集体回答）矩形的面积.

师：在t时间里，两辆车的位移关系如何？

生甲：甲车的位移大于乙车的位移.因为甲车的平均速度比乙车大.

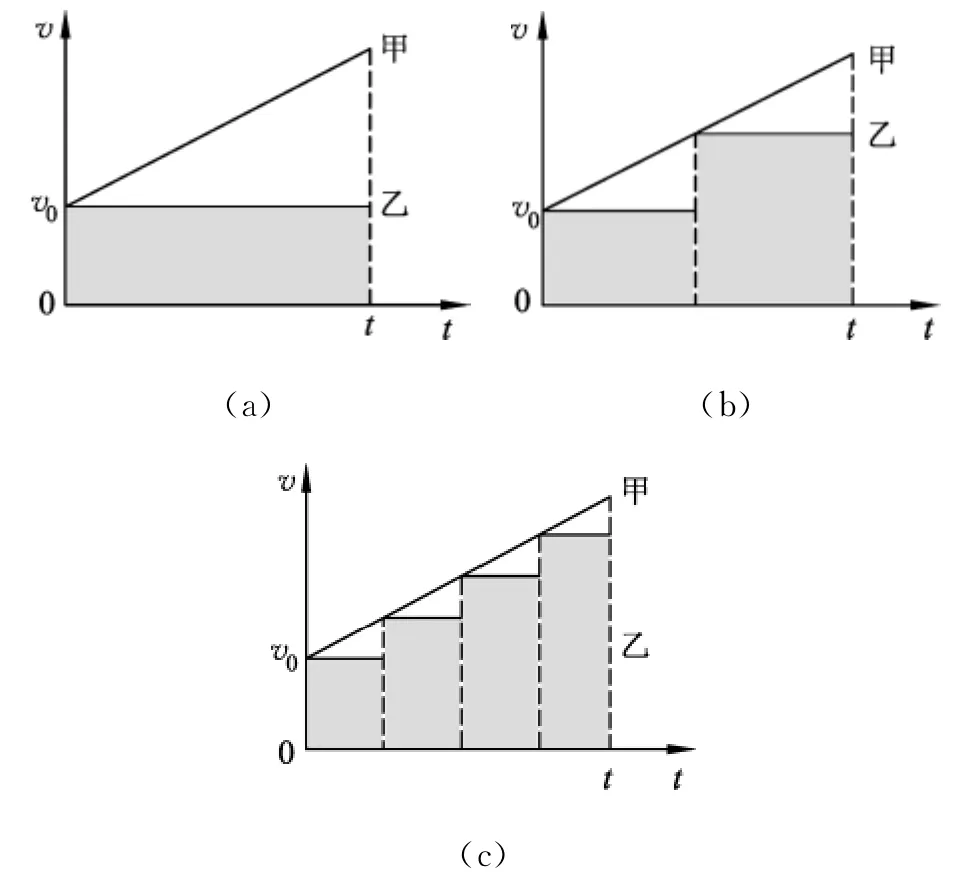
图2

师：如果乙车运动变为两段匀速直线运动，如图2（b）所示，乙车的位移怎么求？

生乙：两块矩形面积的和！

师：如果乙车的运动变成四段匀速直线运动，如图2（c）所示呢？

生：（集体回答）4块矩形面积的和.

师：乙车的运动还可以变成8段匀速直线运动.

生：（集体回答）8块矩形面积的和.

师：乙车的运动还可以变成16段、32段，甚至比可以想象的分段还要多，乙车的位移还是可以用一个个矩形的面积和来表示.

师：当分成足够多的等分时，乙车的位移可以用图线与t轴包围的面积来描述.

师：此时乙车在做什么运动？

师：乙车就是在做与甲车完全相同的匀变速运动，这才是真正的大智慧啊.

在该教师的实际教学中，特意设置了“甲车”和“乙车”两个模型，让学生有了一些“可触摸”、“可比较”的感觉；在乙车的运动变化中，特意具体讨论了从一段的匀速直线运动变化为2段的、4段的、8段的匀速直线运动，而且不厌其烦地在v－t图中画出对应的图线，就好像在学生脚下垫起一层层台阶，引导学生一步步逼近“比可以想象的分段还要多”的境界，这就是教师的“大智慧”.

“化繁为简”，要让学生学习高效率的理解和记忆.在分析匀变速直线运动的几个计算式时，除了帮助学生找到各个表达式中所包含的物理量时，更是特意强调了各个表达式中不包含的物理量.记忆“4个有关量”还是记忆“1个无关量”？无疑后者具有更大的优越性.

“化繁为简”还有一个重要的思想，即不要增加学生无谓的认知负荷.尽管所有的教师都知道在介绍v－t图线的面积对应位移x的问题上采用的是“微元法”，但是该教师在课堂教学中还是回避了“微元法”这三个字，因为这个名词本身并不是本节课的重点，新名词的出现只会增加学生的学习负担.

每个教师都希望学生轻松掌握学习中的难点，其中的技巧确实是值得好好学习和体会的.

3 因材施教的教学理念

“因材施教”是千百年来经过实践验证的经验，因此一节好课总是面对特定的教学对象来设计的.

“因材施教”，尤其要对优秀的学生重视思路的开拓.一般来讲，通常教师在讨论完匀变速直线运动v－t图线中面积S与物体位移x的对应关系后，直接利用梯形面积公式导出位移时间计算关系就可以了.但是该教师在这里独辟蹊径的拓展了学生对几何图线的分析，提供了以下4种面积的求解方法，并让学生有了更多的收获.

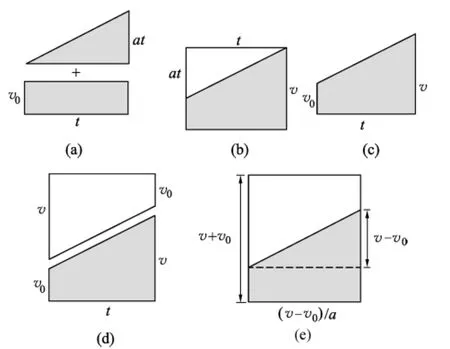
图3

方法1（如图3（a））：梯形面积可以视为矩形面积与三角形面积的和，可以推出

方法2（如图3（b））：梯形面积可以视为大的矩形面积与三角形面积的差，可以推出

方法3（如图3（c））：直接利用梯形面积公式，可以推出

同时和x＝¯vt对比，可以得到

不过（4）式这个平均速度公式仅适用于匀变速直线运动.

方法4（如图3（d）和图3（e））：利用两个梯形能拼为一个矩形，其中图3（e）可以得到

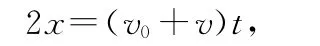
即与（3）式相同的结论.图3（e）中的面积关系为

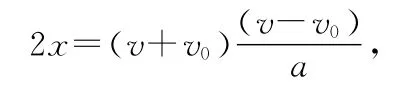
即为匀变速直线运动的重要推论

几何关系的不同运用，可以得到以上5个关系式，其中（5）式的导出更是独辟蹊径，令人叫绝.尽管该教师在课堂中诙谐地将这些结论的导出定位为“小聪明”，但无疑开拓了学生的思路，同时也潜移默化地强化了学生利用图线的意识.

通常（5）式的导出要用另一节课来完成，但是该教师面对成志班学生（一个较为优秀的学生群体），注意到学生较好的接受能力以及较充分的预习情况，大胆地在这节课中利用几何关系导出结论，保证了让优秀学生“吃饱”、“吃好”.

“因材施教”，还要视学生的水平给出学生能力范围内的独立思考空间.在该教师的课堂教学中并不是面面俱到的，比如前面提到的匀变速直线运动的x－t图线，有能力的学生会将初中所学的抛物线和后面推导出的位移时间公式（1）式相联系，从而得到验证.

一节好课不在于一个或者几个亮点，课堂的每一个环节及联系都是经过精心考虑和适时应变的.可以说，每一堂好课都是教师教学生涯积淀的结果，每一堂好课都应该有价值层面的追求.