由一道题的错解牵出对质点组动能的理解
金爱兵 董菲菲
(江苏省盱眙中学,江苏 淮安 211700; 江苏盱眙县马坝初级中学,江苏 淮安 211752)
质点组在不同参考系中的动能将会有不同的数值.而在高中物理中,利用系统动能定理或系统机械能守恒列方程时都要表示出质点组的动能.如果没有把质心动能和质点组动能分清楚,学生在以质心为研究对象列方程可能会出现错误.本文根据学生对一道练习题的错误解答和修正来加深对质心动能和质点组动能的理解.
1 提出问题
例题.质量不计的直角形支架两端分别连接质量为m和2 m的小球A和B,不考虑小球的形状.支架的两直角边长度分别为2L和L,支架可绕固定轴O在竖直平面内无摩擦转动,如图1所示.开始时OA边处于水平位置,由静止释放,求小球A在下落过程中的最大速度?
解法1:以小球A、B和支架组成的系统机械能守恒,设连接B球的杆向左偏离竖直方向θ角,此时小球A的速度为v,有

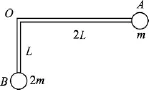
图1
由于单个小球机械能不守恒,系统机械能守恒,于是学生提出了创新解法,将两个球看成是一个球集中在某一点,也就是运用质心的知识.
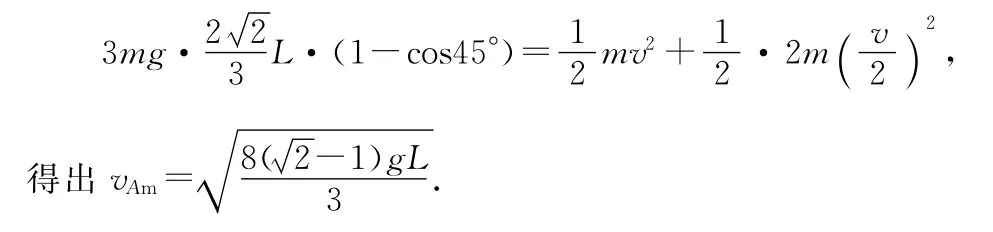
此时另一个学生提出,解法2中方程左边用的是质心势能的减少量,方程右边应该用质心的动能增加量,然后根据质心和小球A都绕O点旋转有相同角速度,找出质心的速度与小球A的速度关系,提出了另一种表达式.
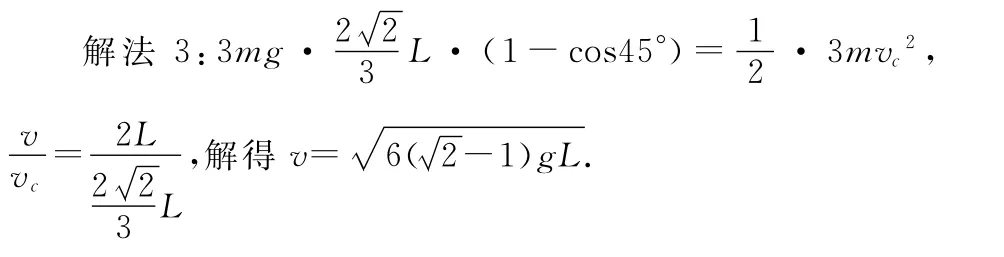
解法3与解法1和解法2的结果不同,问题出在什么地方?
解法2和解法3方程的左边都是质心势能的减少量,方程的右边却不一样,解法2是质点组的总动能,解法3是系统质心的动能,质点组的动能一定等于系统质心的动能吗?
2 分析问题
设质点组中第i个质点在S和S′系中的速度分别为vi和vi′,S′系相对S系的平动速度为u,按照伽利略速度变换有vi=vi′+u.
质点在参照系S中的动能为Ek,则

u是S′系相对S系的速度,也就是质心在S系中的速度vc,

结论:质点组在某参照系中的动能等于质点组在质心系中的动能加上随质心整体平动的动能.(表述1)
3 解决问题
将解法3重新修正:
以A球为例,如图2所示,由数学知识得

图2

当质心运动到O点正下方时,A球的速度vA=v,垂直OA,B球的速度,垂直OB,质心的速度垂直OC.将vA分解为v1沿AC方向和v2垂直AC方向,将vC分解为v3沿AC方向和v4垂直AC方向.
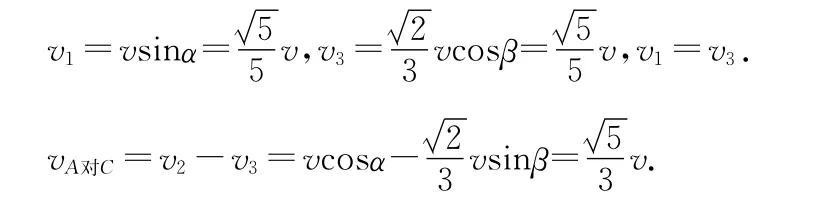
A、B两球对O点的总动能为
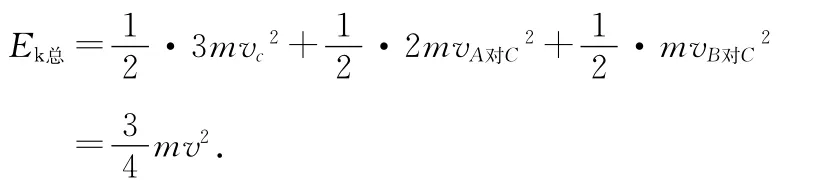
解法3中的机械能守恒方程应更正为
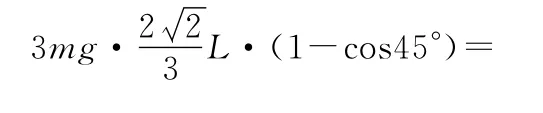
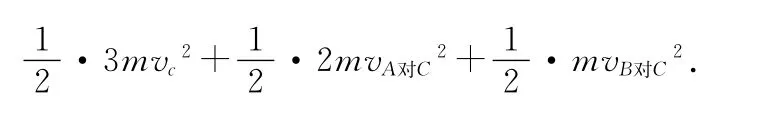
4 拓展问题
将上述结论应用于两个质点组成的质点系.
设两质点相对于参考系S和平动质心参考系S′的速度分别为v1、v2、v1′、v2′,两质点在参考系S 和平动质心参考系S′的相对速度相等为u,即
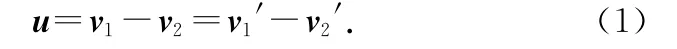
在质心参考系S′中,质点系的总动量为0,有

上述结论可表示为:两个质点构成的质点组动能等于两质点的相对动能加上质心平动的动能.(表述2)
上题可用表述2列方程:小球A和B的速度相互垂直,两者的相对速度和相对动能为
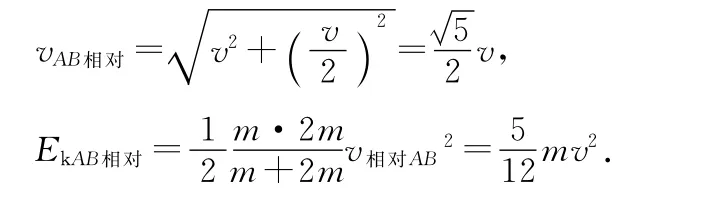
机械能守恒方程为
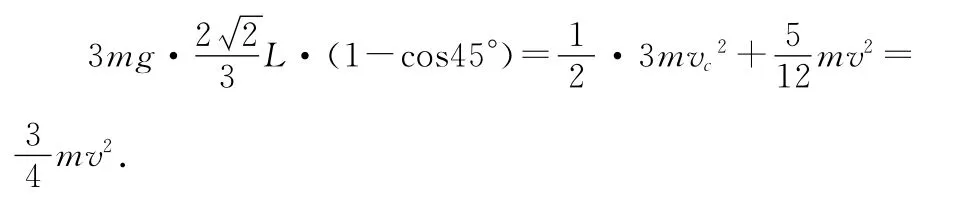
——兼谈参考系与坐标系的关联关系

