带电压反馈的ESO发电机励磁系统滑模变结构

李天云，韩昌兵，朱建华

(东北电力大学电气工程学院，吉林吉林 132012)

带电压反馈的ESO发电机励磁系统滑模变结构

李天云，韩昌兵，朱建华

(东北电力大学电气工程学院，吉林吉林 132012)

针对发电机励磁系统的非线性及易受内、外扰动等特点，应用坐标变换、ESO及滑模变结构控制理论，设计了一种新颖的提高系统动、静态特性的ESO滑模励磁控制器，并在此基础上引入了电压反馈，使其更好地稳定了机端电压，即对系统的状态方程进行坐标变换，然后通过构造扩张状态观察器(ESO)对发电机励磁系统进行动态补偿，实现线性化;采用极点配置法设计滑模切换函数，从理论上保证发电机转子方程具有期望的极点;采用指数趋近率和准滑动模态方法求取滑模控制率。仿真结果表明，该控制器在动态、静态特性上明显地提高了系统的稳定性、快速性和准确性，而且鲁棒性较好。

扩张状态观察器;励磁系统;滑模控制;线性化;鲁棒性

0 引言

在20世纪60年代，用发电机励磁控制提高电力系统稳定性就取得了巨大进步，从那时起励磁控制则成了全面提高电力系统安全稳定性的必选方式。近年来，非线性控制理论有了突破性进展，尤其在电力系统中得到了广泛的应用。基于直接反馈线性化理论、微分几何的非线性最优控制理论等方法［1－3］在励磁控制中也取得了较好的成果。而且，扩张状态观测器［4］的出现为一类不确定系统的反馈确定化提供了一条新思路。因此，基于ESO的自抗扰控制器［5］在中国电力系统多个领域得到推广应用［6－8］。大量实践表明［9－10］:扩张状态观测器在低阶情况下可以有效地估计出较高不确定性非线性系统的内、外扰动。若将被估计出的扰动总和补偿到控制规律中，即可实现动态补偿线性化的目的。

滑模变结构控制［11］是变结构控制系统的一种控制策略，这种控制策略的滑动模态是可以按需要设计的，而且系统的滑模运动与控制对像的参数变化及扰动无关。滑模变结构控制系统的鲁棒性要比一般常规的连续系统强，而且具有响应快速、无需系统在线辨识、物理实现简单等优点。因此，本文在对系统状态方程进行坐标变换的基础上，通过ESO再对系统进行线性化，结合滑模变结构控制理论来设计励磁控制器，将电压反馈引入其中，更好地稳定了机端电压，而且得到的控制规律简洁。单机无穷大系统的仿真实验表明，设计的电压反馈ESO滑模控制器与传统的控制器相比，在响应时间以及鲁棒性方面均有很大改善，提高了系统动态、静态的稳定性、快速性和准确性。

1 励磁系统的数学模型及变换

1.1 数学模型

单机无穷大励磁系统三阶模型为［12］

式中:H为转动惯量;pe与pm分别为电磁功率、机械功率;δ为发电机功角;ω为发电机转速;D为阻尼系数;E'q为q轴暂态电势;Eq为q轴电势;Ef为励磁的控制输入;Td0为发电机定子开路时励磁绕组的时间常数;VS为无穷大母线电压;Xd与X'd分别为发电机的d轴同步电抗和暂态电抗;Xd∑及X'd∑分别为计入了输电系统总电抗后的d轴总同步总电抗与暂态总电抗。

1.2 坐标变换

对单机无穷大励磁系统模型可以写成标准仿射非线性形式:

由于整个系统的非线性主要由变量pe引起，故引入新的状态变量Δpe=pe－pe0，根据非线性系统的状态反馈线性化理论选取坐标变换为

由坐标变换的系统方程不难看出，系统的非线性因素都集中到含有控制输入的方程中。所以直接反馈线性化会让控制器的设计变得复杂，本文采用扩张状态观测器观测该部分。

2 扩张状态观测器

ESO是利用非线性函数fhan来设计比系统多一维的状态观测器，以此估计扰动量及系统的非线性动态。对于如下系统 :x(n)=f(x，…，x(n－1))+w(t)+b(x)u，构造扩张状态观测器为

经过扩张状态观测器反馈之后，系统变成线性系统，可以按照线性系统来设计，本文采用的是滑模设计。

3 电压反馈ESO滑模控制器的设计

3.1 滑模变结构控制原理

通过对书签标记方法的应用，设定高中学业水平考试等级，可以有效提高等级标准的科学性与合理性，可行性显著。

3.2 电压反馈的ESO励磁滑模控制器的设计

由于原有非线性系统经过反馈线性化变成式(10)，取切换函数为

系统到达滑模面上时，由s=0得:

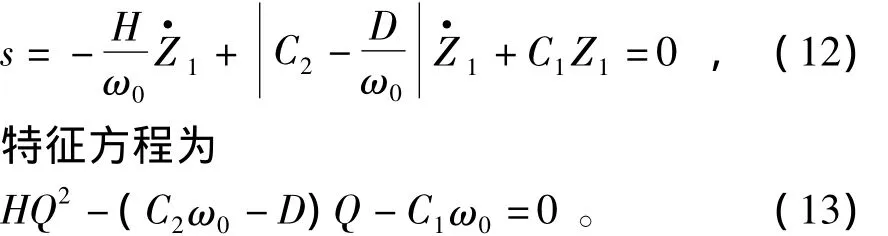
由于Z1=Δδ，设γ1和γ2为发电机转子运动方程的期望极点，则由极点配置法可得:

式中，C1和C2为常数。

采用指数趋近率的控制方式得到滑模控制律V，即

用准滑动模态控制原理，即用饱和函数sat(s)替代符号函数sgn(s)，这样可以更好地减少滑模控制的抖振。sat(s)的表达式为

式中，Δ为边界层。

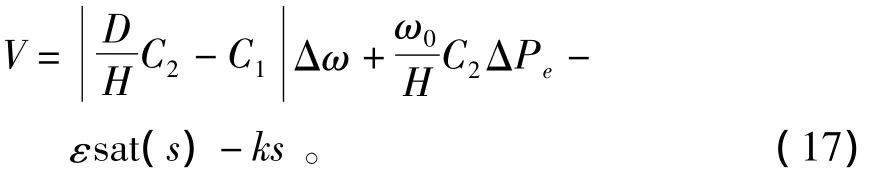
4 仿真研究

本文利用Matlab/Smulink环境对单机无穷大系统进行数字仿真，系统的参数选取:

对该系统进行仿真，假设系统在0.1 s时发电机升压变压器出口高压侧母线的单回路发生三相短路故障，0.2 s时故障清除，带电压反馈ESO滑模控制器(实线)和常规AVR+PSS控制器(点线)2种情况下发电机功角、机端电压、和发电机电磁功率的的响应曲线如图1所示。

从仿真图1可以看出，在常规AVR+PSS的控制器作用下，系统经过较长时间才能平息振荡;而在本文的控制器作用下，系统很快地恢复到平稳状态。显然，说明了该控制器具有明显改善系统动态、静态特征的性能。

系统在小扰动的情况下，本文也做了仿真试验进行比较，在0.1 s时给机械功率施加一个幅值为0.2的阶跃信号。本文设计的控制器(实线)和常规AVR+PSS控制器(点线)2种情况下发电机功角、发电机机端电压与电磁功率的响应曲线如图2所示。

由图2 a可以明显的看出:系统在小扰动情况下，传统的AVR+PSS控制器使发电机功角偏离扰动前的状态，而本文设计的控制器可以快速地使功角恢复到初始稳态值。从图2的其它两个子图中也明显看出带电压反馈的ESO滑模控制器更好地维持了系统的动态、静态特性，再次验证了本文所设计的控制器优越性。

5 结论

通过ESO结合滑模变结构控制设计的控制器无需系统在线辨识、响应快速，实现了系统的线性化，提高了对发电机励磁系统模型的刻画能力。仿真结果表明，在系统遭受不同的扰动下，该控制器仍能保证系统良好的动态、静态性能。

有必要指出，该控制器趋近律参数选取关系着系统到达滑模面的抖振程度，因而对系统的动、静态特性也具有一定的影响。

［1］GALAZ M，ORTEGA R，BAZANELLA A S，et al.An energyshaping approach to the design of excitation control of synchronous generators［J］.Automatica，2003，39(1):111 －119.

［2］李文磊，井元伟，王明顺，等.电力系统稳定控制综述［J］.控制与决策，2002，17(6):833 －838.

［3］GORDON M，HILL D J.Flexible nonlinear voltage control design for power systems［C］//Control Applications，2007.CCA 2007.IEEE International Conference on，2007:1097－1102.

［4］韩京清.一类不确定对象的扩张状态观测器［J］.控制与决策，1995，10(1):85 －88.

［5］韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008.

［6］林飞，张春朋，宋文超，等.基于扩张状态观测器的感应电机转子磁链观测［J］.中国电机工程学报，2003，23(4):145 －147.

［7］黄焕袍，武利强，韩京清，等.火电单元机组协调系统的自抗扰控制方案研究［J］.中国电机工程学报，2004，24(10):168－173.

［8］夏长亮，李正军，杨荣，等.基于自抗扰控制器的无刷直流电机控制系统［J］.中国电机工程学报，2005，25(2):82 －86.

［9］黄一，韩京清.非线性连续二阶扩张状态观测器的分析与设计［J］.科学通报，2000，45(13):1373 －1379.

［10］康忠健，陈学允.非线性扩张状态观测器的一种设计方法［J］.电机与控制学报，2001，5(3):199 －203.

［11］高为炳.变结构控制的理论及设计方法［M］.北京:科学出版社，1996.

［12］刘取.电力系统稳定性及发电机励磁控制［M］.北京:中国电力出版社，2007.

［13］刘金琨.滑模变结构控制Matlab仿真［M］.北京:清华大学出版社，2005.

［14］张峦.静止无功补偿器的模糊变结构控制方法研究［D］.保定:华北电力大学，2007.

［15］卢强，梅生伟，孙元章.电力系统非线控制(第2版)［M］.北京:科学出版社，2008.

Sliding mode of ESO generator excitation system with voltage feedback

LI Tianyun，HAN Changbing，ZHU Jianhua
(School of Electrical Engineering of Northeast Dianli University，Jilin 132012，China)

Since generator excitation system is nonlinear and easy to be influenced by internal and external perturbation，this paper designs a new ESO sliding mode excitation controller to enhance system dynamic and static characteristic by applying coordinate transformation，ESO and sliding mode control，on the basis of which brings in voltage feedback that better stabilizes terminal voltage:transform coordinate of system state equation，then make dynamic compensation for generator excitation system by formulating extended state observer(ESO)，thereby realize linearity;design sliding mode transformation function by pole assignment，which theoretically guarantees the expected pole of generator rotor equation;evaluate sliding mode control ratio by exponent approaching and quasi－sliding mode.Simulation result proves that the dynamic and static characteristic apparently enhances stability，rapidity and accuracy of the system and enjoys great robustness.

extended state observer;excitation system;sliding mode control;linearization;robustness

TM761

A

1002－1663(2012)02－0081－04

2011－11－25

李天云(1945－)，男，教授，研究方向为非线性控制理论在电力系统中的应用。

(责任编辑 郭金光)