从一个物质结构公式说起

崔广杰

（江苏省如皋市丁堰中学 江苏 如皋 226521）

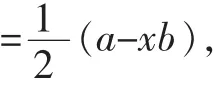
1.对于该公式我们可以作这样的解读，在现代价键理论中，杂化轨道理论在解释粒子空间构型方面是非常成功的，其基本原理是：中心原子的外层原子轨道发生混杂得到总数不变、能量相同的轨道，用于形成σ键和存放孤电子对，这样的σ键键重叠程度大，相互排斥，在三维空间合理分布，达到理想的受力平衡状态，形成稳定的三维立体构型。基于这一理论，ABx型粒子的空间构型取决于中心原子A的杂化类型，杂化类型又取决于A的原子价电子对数，因为两个原子间能而且只能形成一个σ键，故σ键数目为与A直接相连的B原子数x，所以判断杂化类型的关键在于确定A原子上的孤电子对数。对于比较简单的粒子，可依据其电子式中来确定孤电子对数，而对于较复杂的粒子中心原子上孤电子对数的判断，该公式充分的显示了它的优越性。

当中心原子A提供部分价电子与原子B成键，无论是形成σ键还是形成π键，剩下的价电子就是中心原子A的孤对电子。而A提供的价电子数就是B能接受的最多电子数，等于B在该粒子中的化合价。对于ABx型阴离子，计算A的孤电子对数时，价电子数a要加上离子电荷数；对于ABx型阳离子，价电子数a要减去离子电荷数。即使A向B提供孤电子对形成配位键，也不会影响计算结果，这是一种抓总量的计算方法。

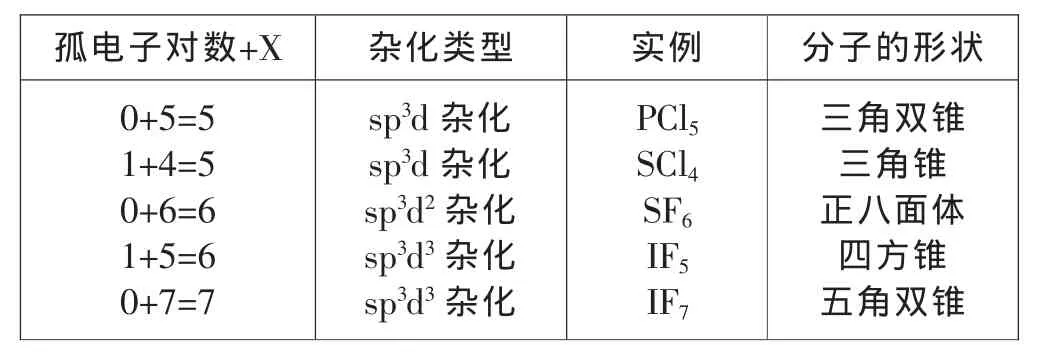
孤电子对数+X 杂化类型 实例 分子的形状0+5＝5 1+4＝5 0+6＝6 1+5＝6 0+7＝7 sp3d杂化sp3d杂化sp3d2杂化sp3d3杂化sp3d3杂化PCl5 SCl4 SF6 IF5 IF7三角双锥三角锥正八面体四方锥五角双锥

在以过渡元素原子为中心的ABx型粒子中，由于次外层d轨道参与杂化，情况比较复杂，所以不能简单的应用该公式计算孤电子对数、确定杂化类型。

3.有时利用上述公式计算孤电子对数会出现0.5的情况，有人认为应该用进一法算，即将0.5计为1，将1.5计为2，这有没有道理呢？首先要弄清这个问题成因，其实有时A与B除了形成σ键外，A还可以与两个甚至多个B形成多原子为中心的多电子大π键，而A参与大π键形成的电子数可以是一个也可以是两个，这就导致了计算孤电子对数时出现0.5的情况。

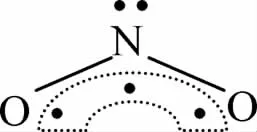
例如NO2分子中，根据上面的公式计算N原子的孤电子对数为0.5，但实际情况是，N原子的最外层电子排布为 2s22px12py12pz1，O原子的价电子排布式是2s22px22py12pz1， 在 NO2分子中，N 原子用 2s与 2px、2py三个轨道进行杂化，得到3个sp2杂化轨道，并用2个sp2杂化轨道分别与两个O原子的2py轨道重叠形成两个σ键，N原子中未杂化的2pz轨道与两个O原子的2pz的轨道平行，垂直于3个sp2杂化轨道所在平面，这三个轨道肩并肩重叠形成3电子3中心的大π键，也就是说N原子成键时“节约”了一个电子，仍然有一对孤电子对，所以NO2分子的结构可以表示为：

我们再来看ClO2的情况，ClO2是V型分子，键角118°，具有顺磁性和很高的化学活性，这些性质可以从ClO2分子的结构中得到解释：Cl的价电子排布式是3s23px23py23pz1，在ClO2分子中，Cl将3s23px23py2杂化，得到3个sp2杂化轨道。成键时O原子将2s22px22py12pz1压缩为2s22px22py22pz0，Cl原子将其中的两个sp2杂化轨道以配位键的形式与两个O原子的空轨道2pz重叠，同时Cl原子未杂化的3pz1与两个O原子的2py轨道平行重叠形成3中心5电子的大π键，故Cl原子只剩下一对孤电子对，再考虑孤电子对对成键电子对的排斥力因素，键角实际为118°。若用上述公式计算，ClO2分子中Cl原子的孤电子对为1.5，计为2的话Cl原子为sp3杂化，显然与事实不符，因为sp3杂化键角应为109.5°，再考虑孤电子对的排斥键角应小于109.5°，而不是现在的118°，ClO2分子的结构可以表示为：

因此，当利用上述公式计算孤电子对出现0.5的时候，要不要“进一”不能一概而论，要具体情况具体分析，毕竟杂化轨道理论是用于解释粒子空间构型，而不是用来确定粒子的空间构型，也就是说在确认粒子的空间构型的事实基础上，可以用杂化轨道理论加以解释，切不可以生搬硬套，现代价键理论才能显示出存在的生命力。

［1］ 北京师范大学无机化学教研室等.无机化学［M］.北京：高等教育出版社，1997