基于混合多项式模型的韶山红色旅游需求人数预测＊

李少游，程 丹，刘利斌

（1.桂林理工大学 旅游学院，广西 桂林 541004；2.池州学院 数学计算机科学系，安徽 池州 247000）

红色旅游是我国20世纪90年代兴起的专项旅游产品，主要是指以中国共产党领导人民在革命和战争时期建树丰功伟绩所形成的纪念地、标志物为载体，以其所承载的革命历史、革命事迹和革命精神为内涵，组织和接待旅游者开展缅怀、学习、参观、游览的主题性旅游活动［1］。它既能发展红色旅游地的经济，创造经济效益，又能让国民增长历史知识、接受教育，促进精神文明建设，创造社会效益。自2004年12月中共中央、国务院布署红色旅游发展规划以来，各级政府和业界人士积极响应，红色旅游蓬勃发展。湖南省依托众多的革命遗址遗迹，开发了大批的红色旅游景点，其中红色韶山的旅游发展更引人注目。随着《2011～2015年全国红色旅游发展规划纲要》的出台，政府对红色旅游的极大重视和对相关纪念活动的宣传推广（如2011年中国共产党成立90周年、2013年毛泽东同志诞辰120周年、2015年抗日战争胜利70周年），未来全国红色旅游的发展势必气势如虹。

为了提高红色旅游研究、规划、管理的科学水平和效力，及时、准确地对其客源进行预测显得尤为重要，因为旅游需求人数是旅游目的地了解旅游需求现状与趋势、掌握旅游市场变化情况的依据。如何准确地预测旅游需求人数，对旅游目的地管理与决策者的意义不言而喻。其实，早在20世纪60年代就有人涉猎旅游需求预测研究，此后对这方面的研究也是日益增多和深入。不少研究人员给出了多种旅游预测方法［2－5］，例如：移动平均法、指数平滑法、自回归移动平均结合法等。随着计算机技术的飞速发展，人工智能理论在旅游预测中也得到了广泛应用［6－8］，如神经网络模型、混沌理论、支持向量机等。

最近，灰色理论［9－12］也被许多国内学者应用于旅游需求人数的预测。用灰色模型对旅游需求人数进行预测，可以解决少信息不确定性问题，结果有一定的可信度。但是灰色预测系统也存在一定的局限性，主要表现在对原始数据的选取要求，要将原始数据作一定的处理后，成为有一定规律的递增曲线才能建模预测。为了解决上述问题，Chu［13］引入三次多项式拟合模型，对一些处于稳定发展期的旅游需求人数进行预测，并与非线性回归和自回归移动平均结合法［3］（ARIMA）进行了比较。在此基础上，笔者以韶山红色旅游景区为例，提出了基于三次多项式和四次多项式的混合多项式预测方法，并与常用的灰色预测模型GM（1，1）的精度进行了比较。

一、多项式拟合模型的介绍

所谓多项式拟合，主要是采用多项式函数形式来进行拟合、来逼近数据所呈现的趋势。下面我们给出多项式拟合的定义。

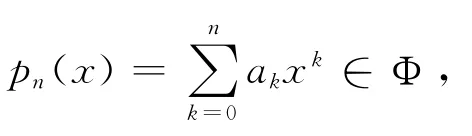
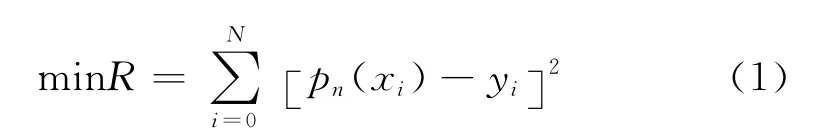
于是，我们把满足（1）式的p n（x）称为多项式拟合函数，R称为最小二乘拟合多项式p n（x）平方误差，可以作为拟合好坏的一个参数。

二、三次和四次多项式拟合模型对韶山景区旅游需求人数的预测

笔者首先分别采用三次和四次多项式拟合模型，对2001～2010年韶山红色旅游景区旅游需求人数的数据进行建模，并与GM（1，1）模型进行了比较，模型的预测结果以及实际值之间的误差见表1，其中2001～2009年所用原始数据都来源于文献［11］，2010年的数据来源于新华网发展论坛。考虑到2003年“非典”突发事件对韶山红色旅游接待的严重影响，我们对2003年数据进行修正，取修正值x2003＝ （x2002＋x2004）/2，实际统计值为185万人次；同理，2005年为国家旅游局确定的“红色旅游发展年”，韶山红色旅游人数比2004年突增了32.6%，同样，我们采用类似的方法对其数据进行修正，取修正值x2005＝（x2004＋x2006）/2，实际统计值为305万人次。

从表1中的数值结果可以看出，三次多项式拟合模型的平均相对误差为6.84%，比GM（1，1）模型的平均相对误差8.30%低1.46%，而四次多项式拟合模型的平均相对误差为2.57%，明显低于GM（1，1）模型的相对误差。且从图1可知，三次多项式拟合模型和GM（1，1）模型的绝对误差相差不大，而四次多项式拟合模型的绝对误差最小。

表1 多项式拟合模型在10年序列旅游人数建模中的计算结果（单位：万人次）

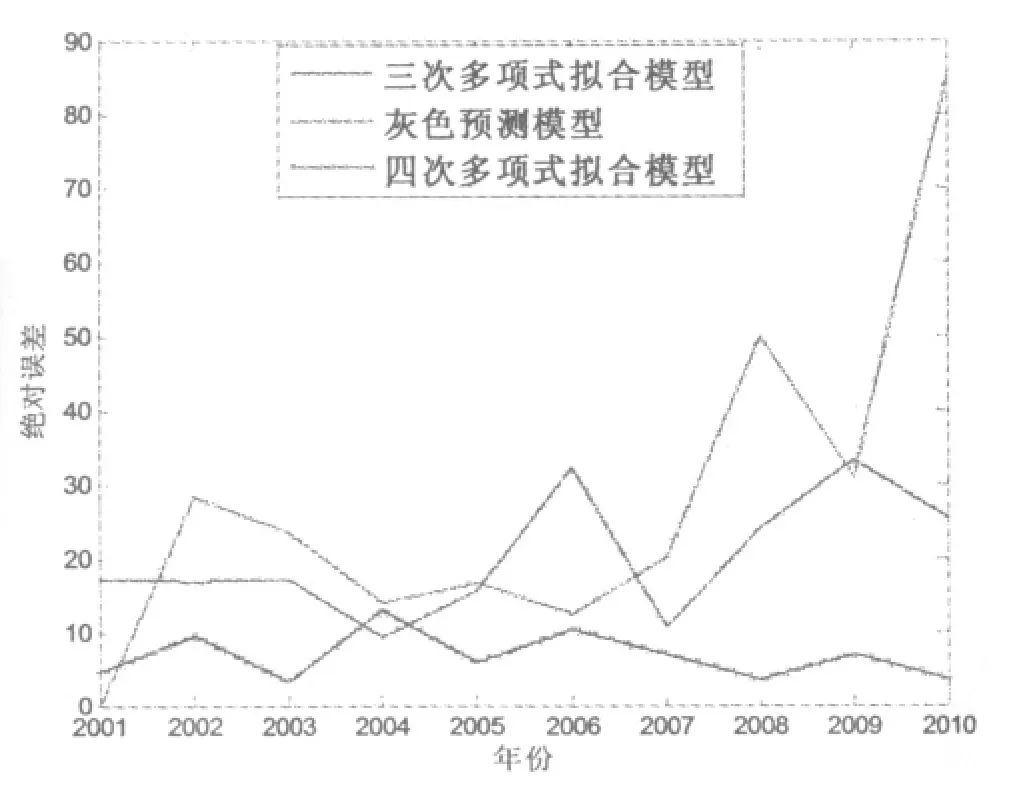
图1 不同预测方法的绝对误差比较

三、混合多项式拟合模型对韶山景区旅游需求人数的预测

（一）韶山2001－2010年红色旅游需求人数建模

综合上述分析，从预测的精度来考虑，四次多项式拟合模型的精度明显高于三次多项式拟合模型和GM（1，1）模型，但是从表1中的预测数据发现，用四次多项式拟合模型预测2002年的人数为164.9万人次，明显低于2001年的数据，这一点与韶山旅游景区近年来旅游人数逐年递增的趋势相违背。而三次多项式拟合模型虽然精度稍微低一些，但是其预测的数据符合逐年递增的趋势。因此，结合这两者的优势，笔者构造出混合多项式拟合模型，在保持预测结果的有效性同时提高其精确性。构造该模型的具体步骤如下：

步骤1：由表1中的韶山红色旅游的原始数据得出如下三次多项式拟合模型

同理可得如下四次多项式拟合模型

其中t表示时间，以2001年为基准，从1开始依次取值；y3，y4分别表示三次和四次多项式拟合模型预测旅游需求人数。

步骤2：取一个权重α∈ ［0，1］，得到如下混合多项式拟合模型

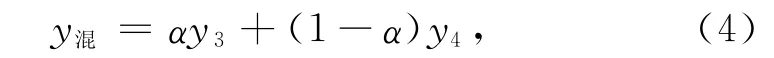
其中y混表示混合多项式拟合模型预测旅游需求人数，当α＝0时，模型（4）为四次多项式拟合模型，当α＝1时，模型（4）为三次多项式拟合模型，即为文［13］中给出的方法。

步骤3：选择合适的α值，使得y混关于时间t为单调递增函数，且预测结果的平均相对误差比较小。

考虑到四次多项式模型的变化率比较快，且为了保证混合多项式模型随着时间t单调增加，混合多项式模型（4）中的α取值应该接近1。于是，本文首先将α取0.9－1，步长为0.01，利用模型（4）进行计算，分别给出2001－2010年韶山红色旅游人数的预测值，然后取其平均值作为当年的预测值，结果见表2。

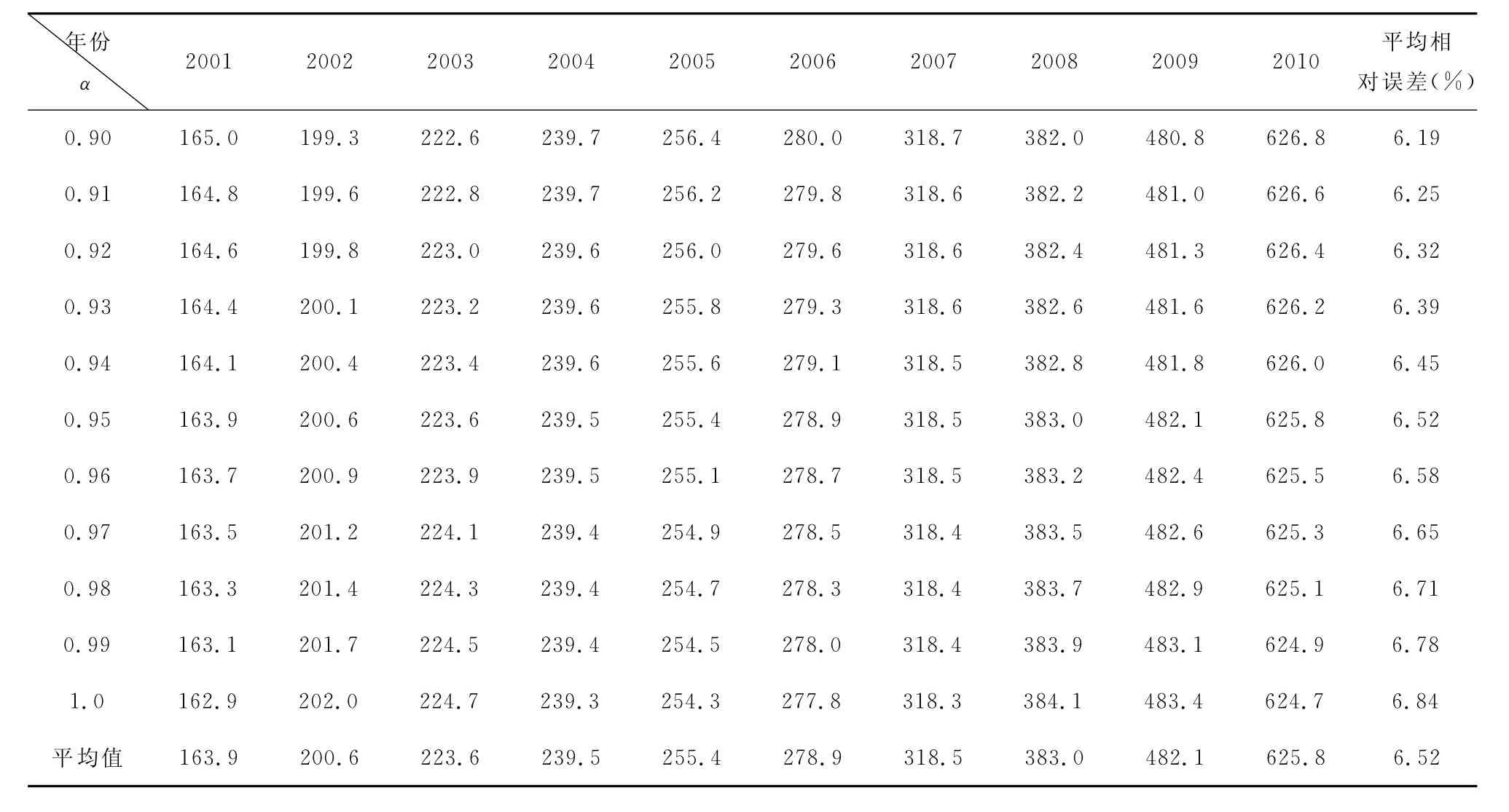
表2 不同α所对应的2001－2010年韶山红色旅游人数预测结果（单位：万人次）

在表2中，我们将最后一行的数值作为2001－2010年韶山红色旅游人数的预测值较为合理，因为其平均相对误差的平均值仅为6.52%，小于GM（1，1）模型和三次多项式模型的平均相对误差，其中比GM（1，1）模型的相对误差8.30%低了1.78%。由此可见，针对韶山的红色旅游人数预测问题，本文提出的混合多项式模型的预测精度要高于GM（1，1）模型和三次多项式模型。

（二）2011－2013年韶山红色旅游需求人数预测

根据混合多项式拟合模型的预测方法，分别利用混合多项式拟合模型和GM（1，1）模型对韶山2011－2013年的旅游需求人数进行预测，具体预测结果见表3。表3中给出了当α取0.9－1时的11组不同的预测值，为了使预测结果更为可靠，我们取这11组预测值的平均值作为最后的预测值。由表3的数据可知，混合多项式拟合模型预测出2011年的旅游需求人数为824.8万人次，而GM（1，1）模型预测出的人数仅为662.7万人次，显然，混合多项式拟合模型预测值更为可信，因为2010年韶山实际的旅游需求人数就已达650万人次，况且2011年为中国共产党建党90周年。又从上文的精度检验结果分析可知，混合多项式拟合模型的预测精度要高于GM（1，1）模型。因此，相对于GM（1，1）模型来说，混合多项式拟合模型的预测结果最为可信。

表3 2011－2013年韶山红色旅游需求人数预测结果（单位：万人次）

四、结论

综上所述，我们可以得到如下结论：

第一，用混合多项式拟合模型对韶山景区红色旅游需求人数预测，可以解决信息呈递增趋势的问题，结果具有一定的可信度。笔者首先分别利用三次和四次多项式拟合模型对韶山景区旅游需求预测进行比较研究。然后分别吸取它们的优点（三次的效度和四次的精度），提出了混合多项式拟合模型，所得模型的预测精度比GM（1，1）模型和三次多项式拟合模型的预测精度要高。该模型的预测结果对韶山红色旅游研究、规划及经营管理具有一定的参考价值。

第二，利用混合多项式拟合模型进行预测，能极大地降低预测的计算量，花费的代价较小。因为混合多项式拟合模型在本质上也是线性模型，算法并不复杂，而且容易被复制和推广应用。

第三，混合多项式拟合模型有一定的局限性。没有一个预测模型完全适用于所有旅游景区的需求预测，也没有任何一个预测模型是永远优于其他的预测模型，只能说是相对更适合而已。同样，相对而言，混合多项式拟合模型适合处于稳定增长期的旅游景区（如文中的韶山红色旅游景区）的需求预测，对于其他处于不同发展期的旅游景区的需求预测还有待研究；而且该模型只适宜做短期预测，对于长期预测，要不断地调整数据并及时修正权重α，以提高预测精度。

［1］田孝蓉.旅游经济学［M］.郑州：郑州大学出版社，2006：33.

［2］Qu H L，Lam S.A travel demand model for Mainland Chinese tourists to Hong Kong［J］.Tourism Management，1997，18（8）：593－597.

［3］Goh C，LawR.Modeling and forecasting tourism demand for arrivals with stochastic no stationary seasonality and intervention［J］.Tourism Management，2002（23）：79－84.

［4］Chu F L.Forecasting tourist arrivals［J］.Journal of Travel Research，1998（36）：79－84.

［5］Kulendran N，Maxwell K L.Forecasting international quarterly tourist flows using error correction and time－series models［J］.International Journal of Forecasting，1997（13）：319－327.

［6］Rob L.A neural network model to forecast Japanese demand for travel to Hong Kong［J］.Tourism Management，1999（20）：89－97.

［7］Rob L.Back－propagation learning in improving the accuracy of neural network－based tourism demand forecasting［J］.Tourism Management，2000（21）：331－340.

［8］李志龙，陈志钢，覃智勇.基于支持向量机旅游需求预测［J］.经济地理，2010，30（12）：2122－2126.

［9］蒋蓉华，刘曲华，焦俊刚.基于灰色动态GM模型与计算机模拟的丽江旅游前景预测［J］.安徽农业科学，2010，38（13）：7116－7118.

［10］刘慧敏，樊锁海.基于灰色系统理论的广州市旅游接待人数预测与分析［J］.统计与决策，2010（17）：64－66.

［11］刘红海，刘建平.基于灰色模型的韶山红色旅游景区客源预测［J］.经济地理，2010，30（6）：1047－1051.

［12］朱晓华，杨秀春，蔡运龙.基于灰色系统理论的旅游客源预测模型［J］.经济地理，2005，25（2）：232－235.

［13］Chu F L.Forecasting tourism demand：a cubic polynomial approach［J］.Tourism Management，2004（25）：209－218.