一个新的三角拟合四阶预估校正方法①

郑 娟

(枣庄学院数学与统计学院，山东枣庄277160)

0 引言

下面形式的一阶微分方程初值问题

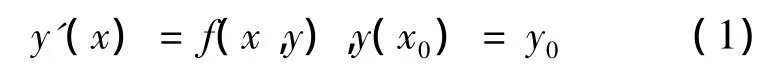
在天体力学、化学物理学、电子学等不同的领域內广泛出现，很多情况下其解具有一定的周期性．如果能对解的主导频率有较准确的估计，常采用变系数方法求这类问题的数值解，三角拟合[1]是其中常用的方法．Vanden Berghe及Simos[2，3]等人对三角拟合Runge－kutta方法作了深入的研究．本文在线性多步法中预估校正方法基础上，利用三角拟合技术，得出了一个新的三角拟合预估校正方法，数值试验表明，新方法在求解周期初值问题时具有明显的高效性．

1 三角拟合预估校正方法

对于的数值求解，考虑下面的预估校正格式[4]

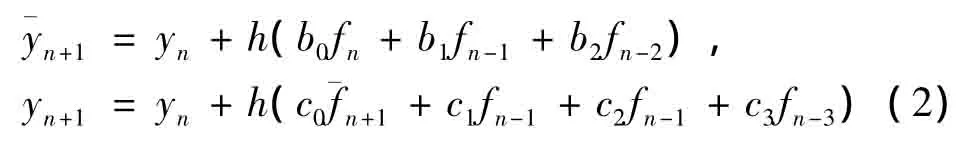
令式(2)的预估格式精确积分{1，x，cos(ωx)，sin(ωx)}的线性组合，得如下方程组

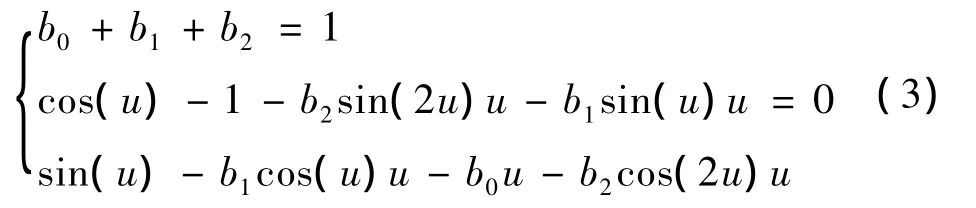
令式(2)中校正格式精确积分{1，x，x2，cos(ωx)，sin(ωx)}的线性组合，得

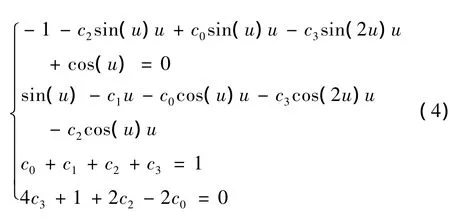
分别解线性方程组(3)与(4)可求得b0，b1，b2与c0，c1，c2，c3．当 u 较小时，应使用它们的泰勒展开式

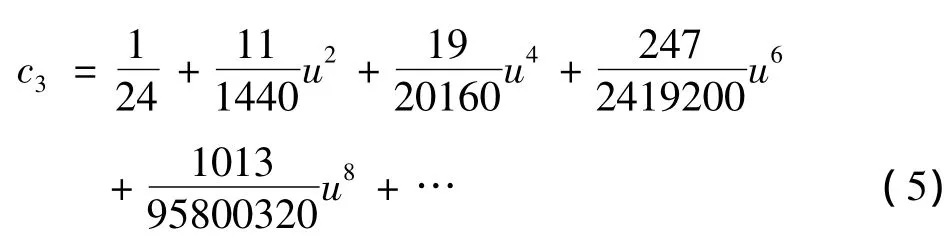
由式(5)确定的三角拟合预估校正格式(2)记为ADM4PCF1N，由式(5)，当 ω→ 0时，新方法ADM4PCF1N将变为原始的预估校正方法[4]．

图1 原始四阶预估校正方法的稳定性区域

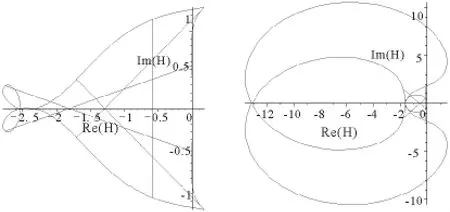
图2 三角拟合四阶预估校正方法分别当u=1，u=8时的稳定性区域

计算y(xn+1)－yn+1可得局部截断误差

故其代数阶为 4．由式(6)，当 y为{cos(ωx)，sin(ωx)}的线性组合时，局部截断误差将消减为0，这也说明新方法ADM4PCF1N可对{cos(ωx)，sin(ωx)}的线性组合精确积分．

2 稳定性分析

将预估校正格式(2)应用到试验方程:

得差分方程

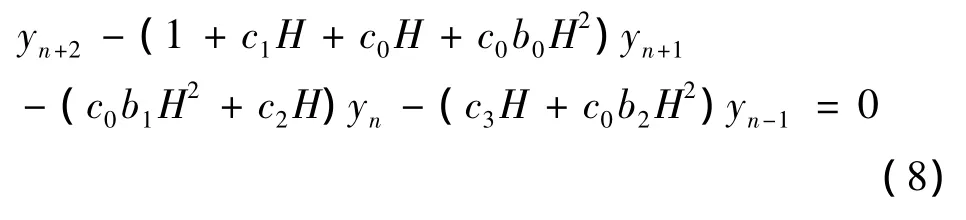
其中H=λh

式(8)的特征方程为

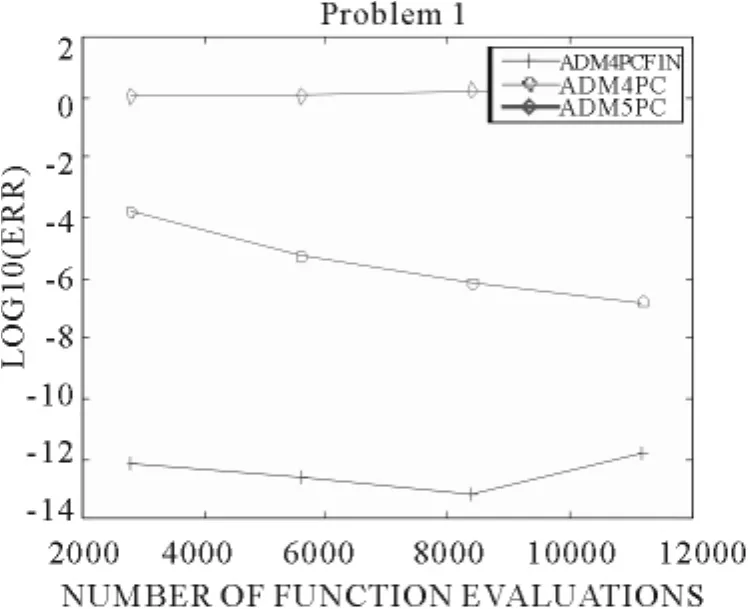
图3 数值实验3．1

图4 数值实验3．2

图5 数值实验3．3

解关于H的方程(9)，用边界轨迹法[5]画出θ∈[0，2π]时的绝对稳定区域．图1与图2分别给出原始四阶预估校正方法与三角拟合四阶预估校正方法分别当u=1，u=8时的稳定性区域．由图2看出，随着频率取值增大，三角拟合四阶预估校正方法的绝对稳定性区域也随之变大．这使得新方法较其它只有较小稳定性区域的方法有很大的优势．

3 数值实验

选用下列三个方法予以比较

四阶预估校正方法[4]，用ADM4PC表示．

四阶预估校正方法[4]，用ADM5PC表示．

三角拟合四阶预估校正方法，即本文得到的新方法，用ADM4PCF1N表示．

评价的标准是比较三个方法的全局误差及计算所用的函数的个数．

3．1 问题1

考虑如下的二体问题:

在计算中，选择区间 0≤ x≤ 100，对方法ADM4PCF1N估计频率，数值运算结果由图3给出．

3．2 问题2

考虑下面初值问题:

其精确解为:

y(x)=cos(10x)+sin(10x)+sin(x)

在计算中，选择区间 0≤ x≤ 100，对方法ADM4PCF1N估计频率ω=10，数值运算结果由图4给出．

3．3 问题3

考虑下面初值问题:

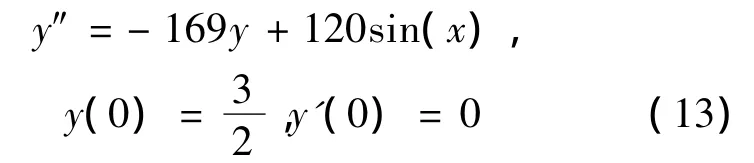
在计算中，选择区间 0≤ x≤ 100，对方法ADM4PCF1N估计频率ω=13，数值运算结果由图5给出．

4 结论

构造了一个处理振荡问题的新的三角拟合四阶预估校正方法，它可以精确积分{cos(ωx)，sin(ωx)}的线性组合．数值试验表明新方法‴应用于求解周期性初值问题时，其性能远好于原始的四阶及五阶预估校正方法．

[1] Ixaru L G，Berghe G V．Exponential fitting[M]．Kluwer Academic Publishers，Dordrecht，2004．

[2] Simos T E．An Exponentially－fitted Runge－Kutta Method for the Numerical Integration of Initial－value Problems with Periodic or Oscillating Solutions[J]．Computer Physics Communications，1998，(115):1－8．

[3] Vanden Berghe G，De Meyer H，Van Daele M，Van Hecke T．Exponentially － fitted Explicit Runge–Kutta Methods[J]．Computer Physics Communications，1999，(123):7 －15．

[4] Hairer E，Norsett S P，Wanner G．Solving Ordinary Differential Equations:Nonstiff Problems[M]．Springer Verlag，Berlin Heidelberg，1993．

[5] Lambert J D．Numerical Methods for Ordinary Differential Systems:the Initial Value Problem[M]．John Wiley ＆ Sons，Inc．，New York，1991．