EXCEL在分布拟合中的应用①

李 晗

(吉林师范大学数学学院，吉林四平 136000)

0 引言

Excel作为一款优秀的数据处理软件，同时也是一款实用的统计分析软件.它在应用统计学中发挥着巨大作用.宋廷山等人的著作[1]充分地说明了这一事实.本文将以南京地区58年来的降雨量为例，以Excel为工具，给出它在分布拟合中的应用方法，数据来源于58238号气象站所观测到的南京地区1951～2008年这58年间的逐日降水资料.

国内学者认为降雨量的变化规律一般服从正态分布或对数正态分布[2]，然而由于不同地区的地形、地貌及气候条件一般不同，因此在处理具体问题时，仍需要具体的分析判断.为了便于说明，我们先将样本数据汇总成年降雨量表，并升序存入Sample.xls中，其中工作表的第一列是序号1～58，第二列是南京地区58年间的年降雨量样本数据(单位:毫米)的升序排列，记样本数据为Xi.

1 利用EXCEL对样本进行描述统计

在Excel软件中打开Sample.xls工作表，执行“工具”→“数据分析”→“描述统计”，在弹出的“描述统计”对话框中，将“输入区域”设置为$B$1:$B$58，“输出区域”设置为 $G$1，单击“确定”可得描述统计见表1.

表1 样本的描述统计表

从表1中可以看出，样本的均值为1051.54，方差为57178.92.样本的偏度系数为 0.75，说明样本的分布为右偏而非对称的，样本峰度系数为1.46，其值不为零，可以初步判定样本不服从正态分布.

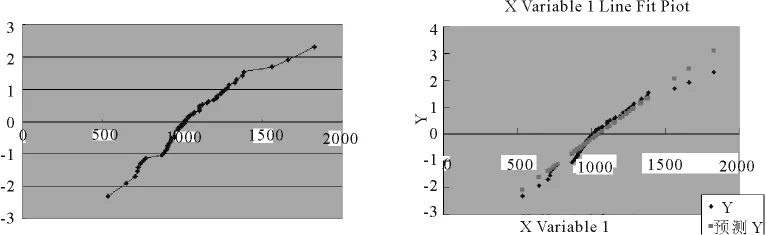
图1 (a)样本数据的正态概率纸散点图 (b)样本数据的正态概率纸线性回归

2 利用EXCEL对样本进行正态概率纸检验

为了进一步判断样本是否服从正态分布，下面利用正态概率纸方法进行检验.

Step1.计算样本的累计频率

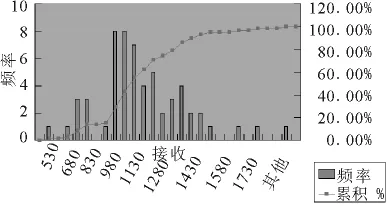
图2 样本频率直方图

Step2.计算样本的累计频率对应的正态分布分位数

在“D1”单元格中输入“=NORMINV(C1，0，1)”并回车，然后将光标定位在“D1”单元格右下角，向下拖动鼠标，完成样本累计频率所对应的正态分布分位数的计算.记相应的分位点为Yi.

Step3.绘制散点图

以Xi为横坐标，Yi为纵坐标利用Excel绘制散点图.将光标定位到Sample.xls工作表的“I1”单元格，执行“插入”→“图表”→“XY散点图”命令，选择“平滑线散点图”，单击“下一步”，在“数据区域”中输入数据区域为“=Sheet1!$B$1:$B$58，Sheet1!$D$1:$D$58”，单击“确定”，便可得到样本数据在正态概率纸图上的散点图，如图1(a)所示.

Step4.绘制Xi和Yi的回归直线

执行“工具”→“数据分析”→“回归”命令，在弹出的“回归”对话框中设置Y值输入区域为:“$D$1:$D$58”，X值输入区域为:“$B$1:$B$58”，输出区域为:“$F$27:$N$37”.可得回归直线如图1(b)所示.

从图1可以看出，样本两端数据明显偏离了回归直线，从而可以断定，样本不服从正态分布.

3 样本分布函数的确定

为了确定样本的分布函数，先利用Excel软件绘制样本的直方图，再进行进一步的推断和检验.

Step1.利用Excel绘制直方图

由表1知样本最小值和最大值分别为534.6和1825.8，以530为起点，以50为组距进行分组共分26组.在“B60”单元格中输入530，在“B61”单元格中输入580并向下拖动鼠标，直至数据填充到1830.将此数据作为分组的接收区域.执行“工具”→“数据分析”→“直方图”命令，在弹出的“直方图”对话框中设置输入区域为:“$B$1:$B$58”，接受区域为:“$B$63:$B$89”，输出区域为:“$C$63:$E$89”，并勾选“累计百分率”和“图表输出”两项，得到频率分布表(略)和直方图如图2所示.

Step2.对样本进行对数变换

由图2初步推测样本服从对数正态分布.为了进一步检验结论的正确性，需先对样本数据进行对数变换，若变换后的数据服从正态分布，则可以断定原样本服从对数正态分布[3].在 Sample.xls工作表的“E1”单元格中输入“=ln(B1)”并向下拖动单元格完成对样本进行对数变换.

Step3.检验对变换后样本的正态性

再次应用本文第2节中的方法对变换后的样本数据进行正态性检验.得到变换后数据的正态概率纸散点图如图3(a)所示和正态概率纸线性回归图如图3(b)所示.

从图3可以看出，对数变换后的样本几乎在处在同一直线上，从而可以断定，原样本服从对数正态分布.

Step4.估计分布参数

文献[4]讨论了对数正态分布的最大似然估计方法.设总体X服从参数为μ和σ2的对数正态分布，X1，X2，…，Xn是来自总体X的简单随机样本，记μ和σ2的最大似然估计量分别为，根据文献[4]的结果，有

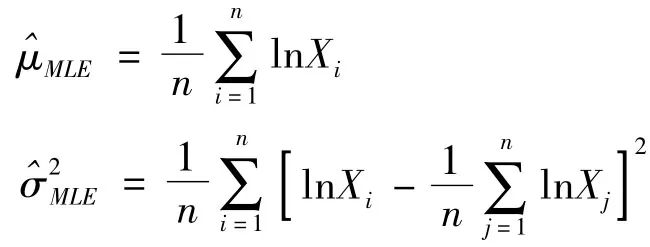
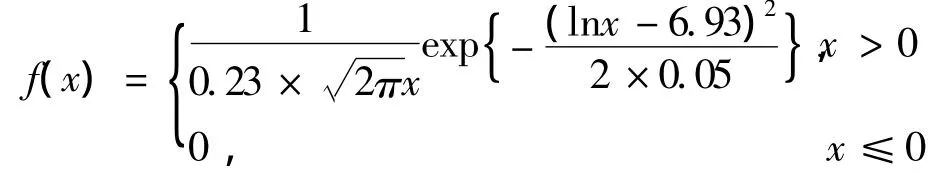
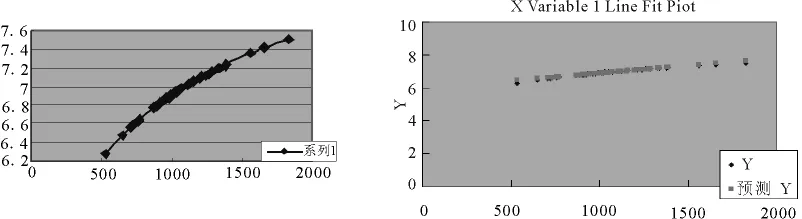
图3 (a)对数样本的正态概率纸散点图 (b)对数样本的正态概率纸回归直线

在Matlab中对样本数据进行Kolmogorov－Smirnov检验，p值为0.46，这进一步说明了本文结果的正确性.

[1]宋廷山，吴风庆，尉雪波.应用统计学:以Excel为分析工具[M].成都:西南财经大学出版社，2006.

[2]袁兴仁.兰州地区年降水量的分布函数[J].西北师范大学学报(自然科学版)，1990(2):69－71.

[3]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社，2004:120，363.

[4]于洋，孙月静.对数正态分布参数的最大似然估计[J].九江学院学报，2007(6).