一类具无穷时滞和收获率捕食－食饵系统的多重周期正解①

谢 东

(亳州师范高等专科学校理化系，安徽亳州236800)

生物种群系统的持续生存和正周期解的存在性都是重要的研究课题，历来受到学术界关注，许多学者已经进行了深入研究，并取得了许多结果[1－5]．本文研究具无穷时滞、收获率和非单调功能性反应函数的比率依赖捕食－食饵系统．

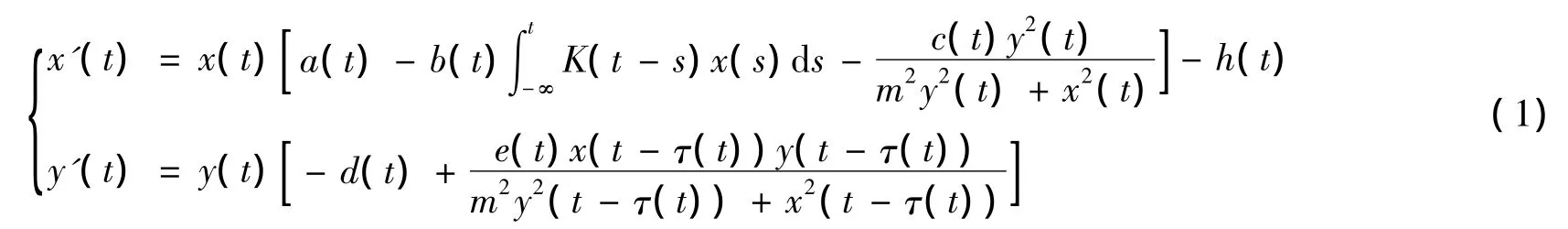
其中 a(t)，b(t)，c(t)，d(t)，e(t)，h(t)，τ(t)是非负连续的 ω周期函数，m是一个正常数，K(s):+→+是可测的ω周期函数且满足正规化假设，即有

本文利用重合度理论研究系统(1)的多重周期正解存在性，得出了对系统(1)的多重周期正解存在性是与食饵种群的收获率有关的新结果．

1 准备知识

有关重合度理论及延拓引理请参考文献[6]．

引理1．1[6]设L是指标为零的Fredholm映射且Ω为X中的有界开集，N在上是L－紧的．假设

(1)对任意的λ∈(0，1)，方程Lx=λNx的解满足 x ∉ ∂Ω(这里 ∂Ω =Ω);

(2)对任意的x∈∂Ω∩Ker L，QNx≠0;(3)Brouwer度deg{JQN，Ω∩Ker L，0}≠0，这里的J，Q如上定义;

引理1．2[5]若f(t)是一连续的 ω － 周期函数，那么

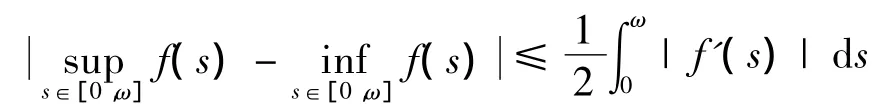
为了方便叙述，再引入下面记号:

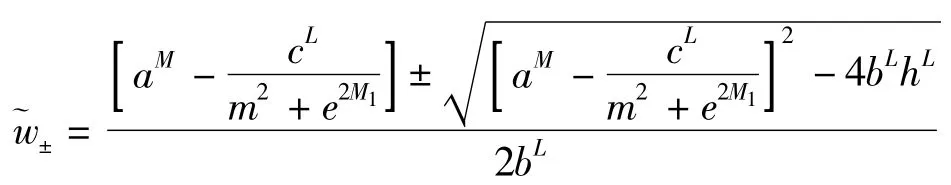
不难证明q－＜l－＜l+＜q+，w－＜v－＜v+＜w+和

2 正周期解存在性

定理2．1 在系统(1)中，若系数函数满足

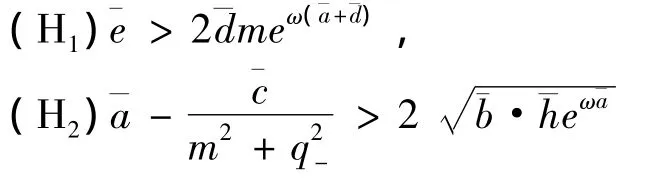
则系统(1)至少存在四个ω－周期正解．

证明: 作变换

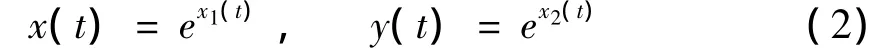
则系统(1)可化为

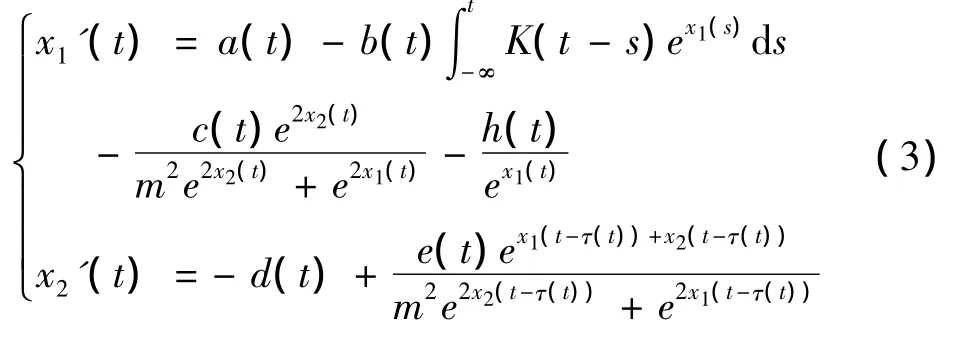
作变量替换

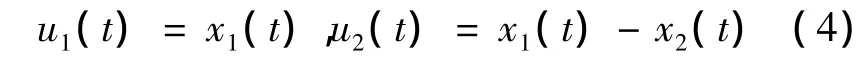
则系统(3)可化为

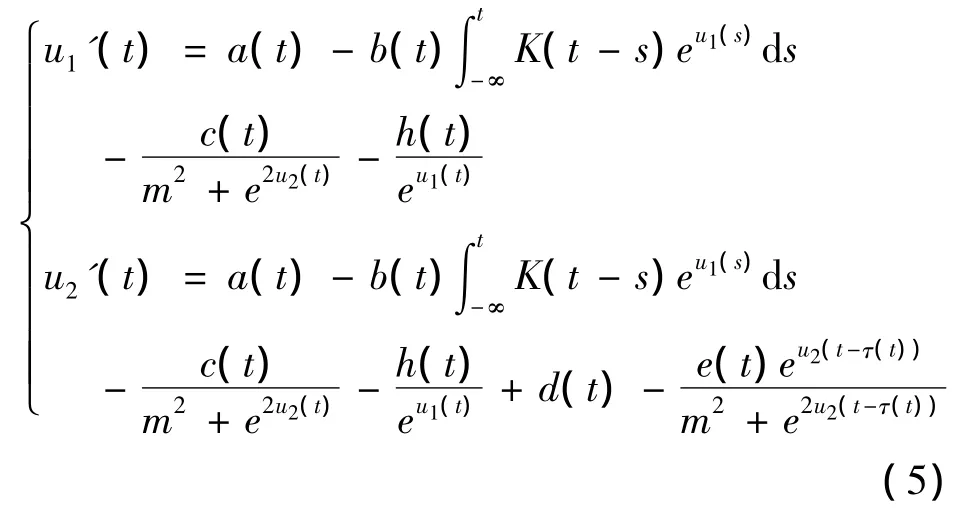
为方便起见，在以下证明中记

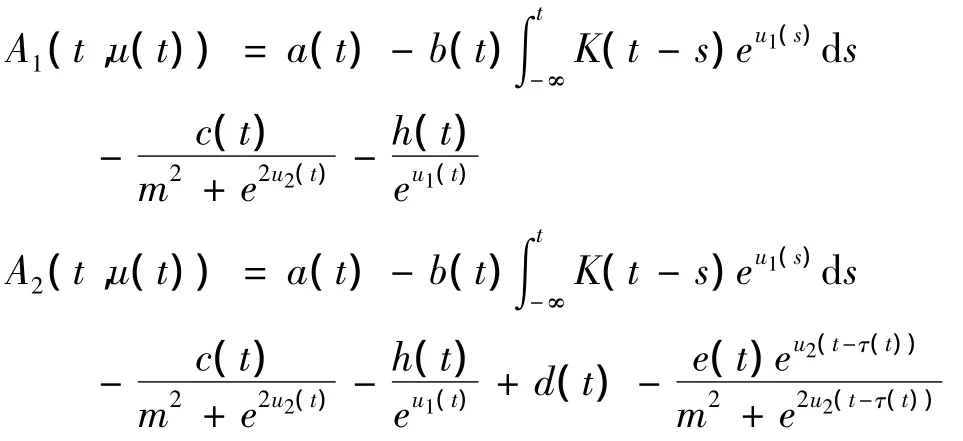
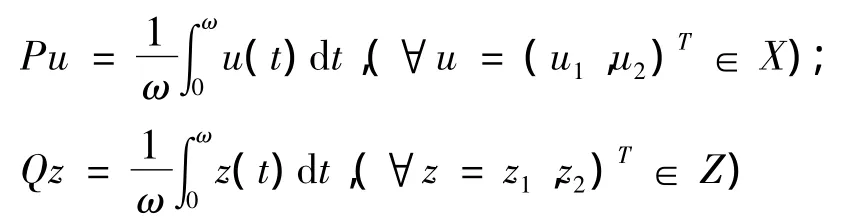
令 X=Z={u=(u1，u2)T∈ C( ，2):ui(t+ ω)=ui(t)，i=1，2，}，并令，u1(t)|，|u2(t)|}，则X，Z在范数‖·‖下是一个Banach空间．现定义线性算子L:Dom L⊂X→Z如下:Lu=u'，(∀u∈Dom L⊂X);又定义算子N:X → Z 如下:Nu=(A1(t，u(t))，A2(t，u(t)))T，(∀u=(u1，u2)T∈X);又定义投影算子P:X→X及Q:Z→Z如下:易见Ker L={u∈X:u=h∈2}，Im L={z∈为 Z 中的闭子集，且dim Ker L=n=co dim Im l，故L是指标为零的Fredholm映射．P，Q是连续投影且使得Im P=Ker L，Im L=Ker Q=Im(I－Q)，X=Ker L⊕ Ker P，Z=Im L ⊕ Im Q．记 Lp=ΔL|Doml∩KerP，则 LP:Dom L∩Ker P→Im L是到上的一一映射．因此L的广义逆映射KP:Im L;→Dom L∩Ker P存在，且

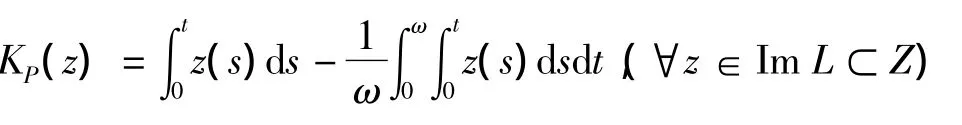
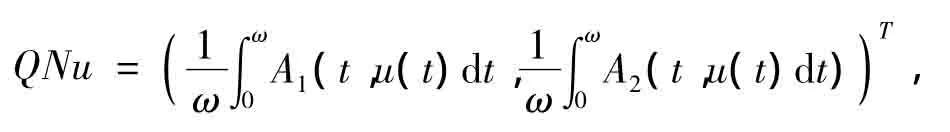
由于

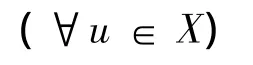
所以

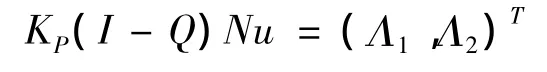
其中

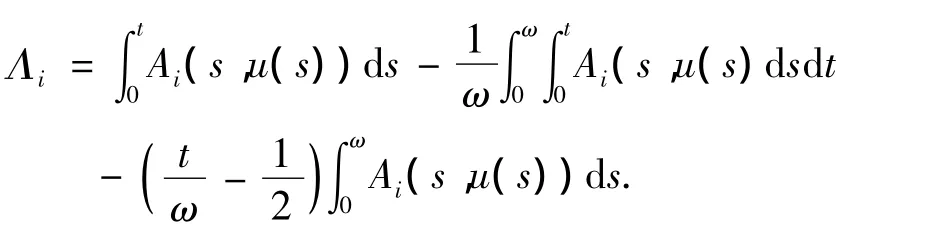
利用Lebesgue收敛定理可以证明QN和KP(I－Q)N是连续的，又利用Arzela－Ascoli定理可以证明，对X中的任意开子集Ω，QN()及KP(IQ)N)分别是Z及X中的紧子集．因此，对于X中的任意有界开子集Ω，N在上是L－紧的．

为了应用引理1．1，需要至少找四个X中的有界开集 Ω1，Ω2，Ω3，Ω4．为此考虑算子方程 Lu=λNu，λ ∈ (0，1)，有

设u=(u1(t)，u2(t))T∈X是系统(6)对应于某一λ∈(0，1)的解，将(6)式两端从0到ω积分得

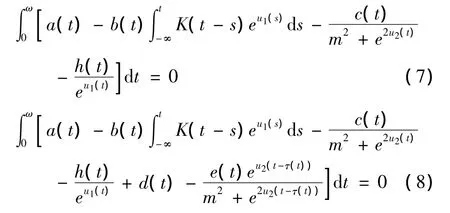
由(7)～(8)式有

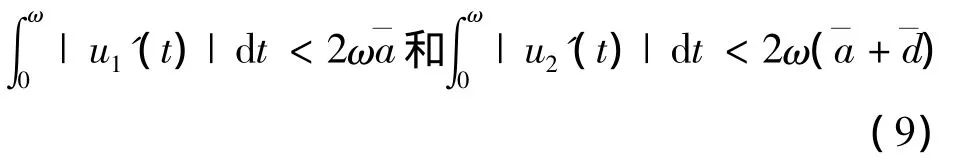
因为 u=(u1(t)，u2(t))T∈ X，故存在 ηi，ζi∈[0，ω]使得

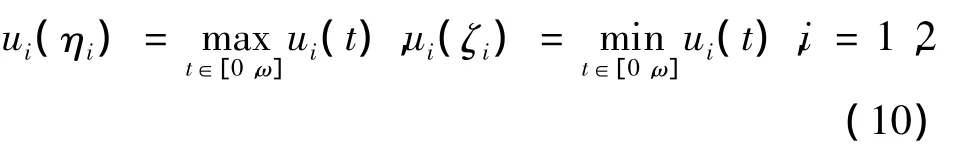
首先估计ui(t)(i=1，2)的先验界．由(10)与(8)式可得

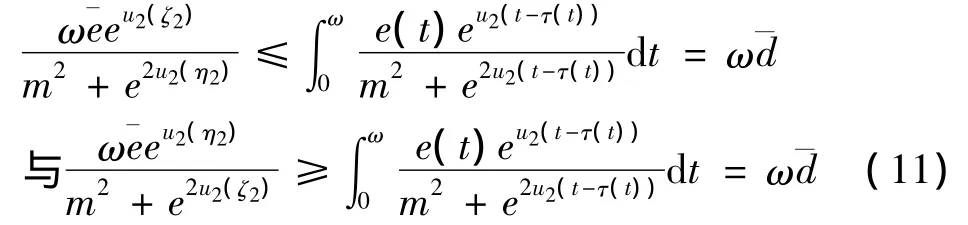
另外，由(9)－(10)以及引理1．2知

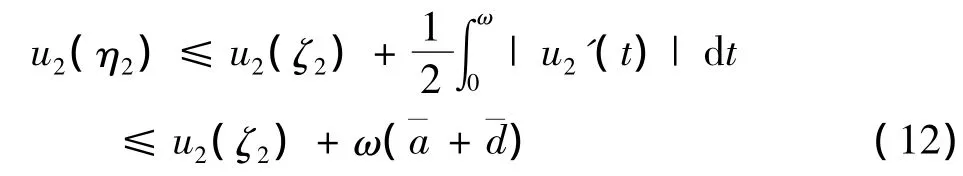
将(12)代入到(11)的两个式子中，并整理可得

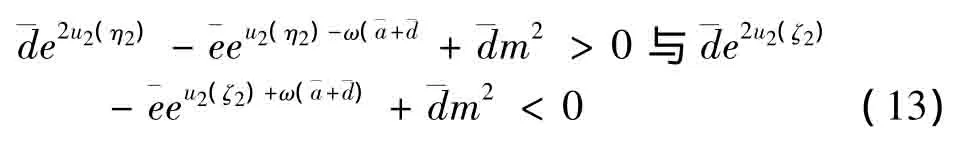
由条件(H1)以及(13)的两个式子有

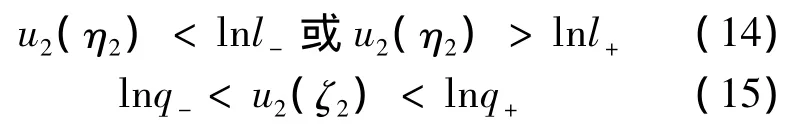
由(12)和(15)知，对∀t∈[0，ω]有

另一方面，由(7)，(10)，(15)和(16)可得

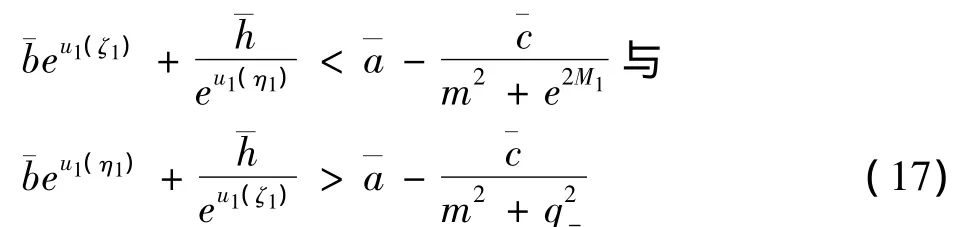
另外，由(9)，(10)以及引理1．2知

将(18)代入到(17)的两个式子中并整理可得

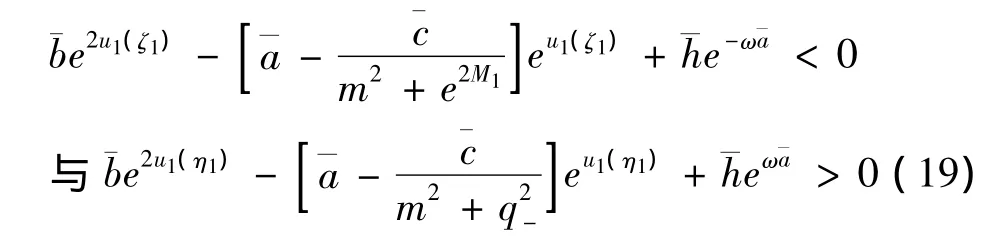
由条件(H2)以及(19)的两个式子有

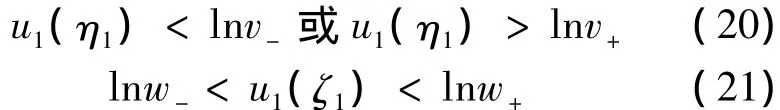
由(21)，(18)知，对 ∀t∈[0，ω]有

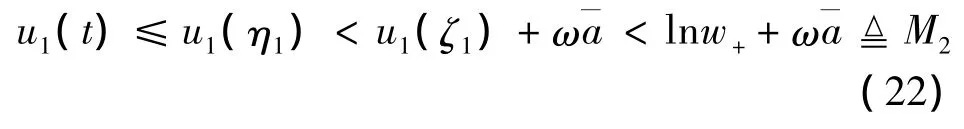
显然，正常数 lnl±，lnq±，lnv±，lnw±，M1，M2与 λ(λ∈(0，1))是无关的．

取

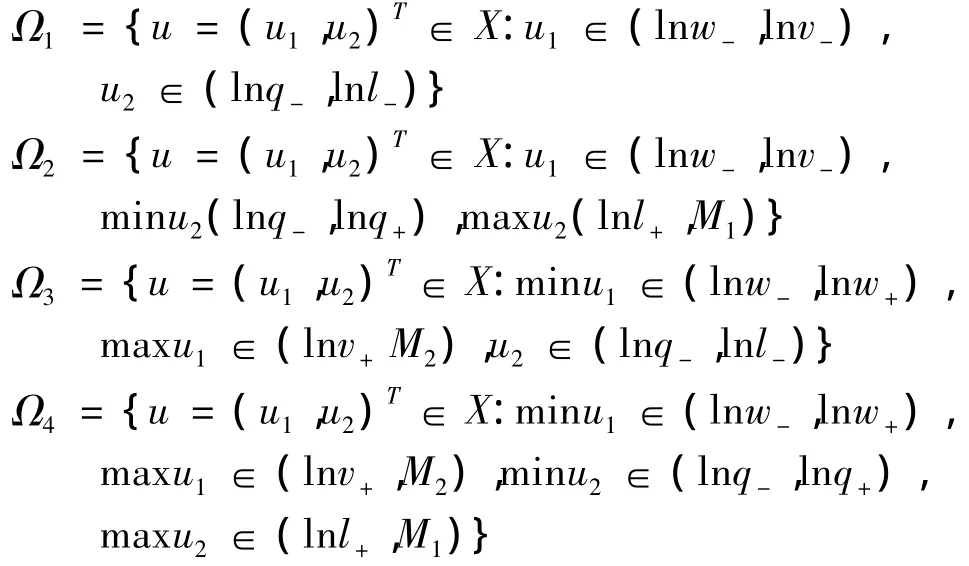
显然Ωi(i=1，2，3，4)是X中的有界开子集，且Ωi∩ Ω，j= Φ(i≠ j;i，j=1，2，3，4)．则 Ωi满足引理1．1 中的条件(1)．

易证Ωi(i=1，2，3，4)满足引理1．1中的条件(2)．

接下来我们证明 Ωi(i=1，2，3，4)满足引理1．1中的条件(3)．为此，我们定义映射族Φ:Dom L×[0，1]→ X 为

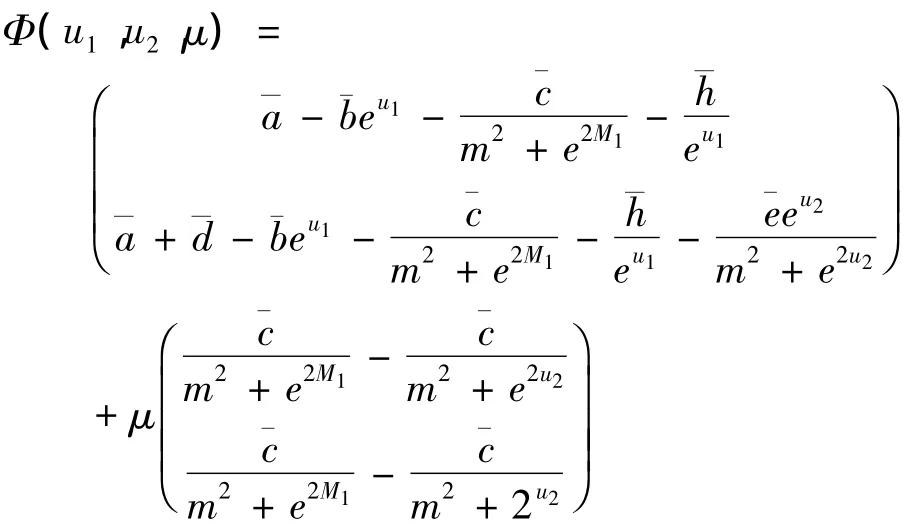
其中μ∈[0，1]为参数．不难证明当u=(u1，u2)T∈ ∂Ωi∩ ker L= ∂Ωi∩2，μ ∈[0，1]时，Φ(u1，u2，μ)≠ 0．

另外，注意到代数方程

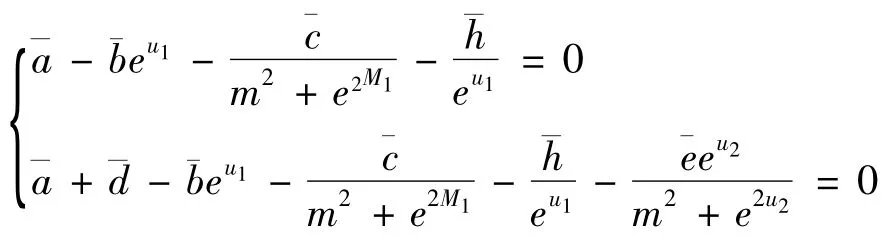
有四个实根:

取J:ImQ→X为恒等映射，经计算可得

deg{JQN，Ωi∩ Ker L，0}≠0(i=1，2，3，4)即证Ωi(i=1，2，3，4)满足引理1．1中的条件(3)．因此系统(5)至少有四个ω－周期解u*(t)∈Dom L∩1，u*＊(t)∈Dom L∩2，u*＊＊(t)∈Dom L ∩3和 u*＊＊＊(t)∈ Dom L ∩4．从而系统(1)至少存在四个正的ω－周期解．

定理2．2 在系统(1)中，若系数函数满足

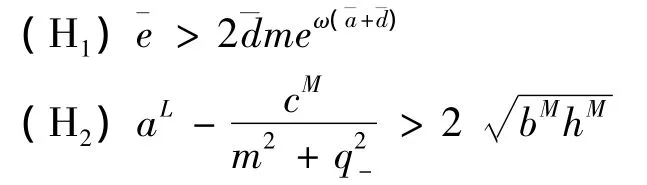
则系统(1)至少存在四个ω－周期正解．

证明: 除了系统(6)的解的先验界估计(关于u1(t)的上、下界)与定理2．1中的不同之外，定理2．2的证明与定理2．1的证明相类似．

由(11)知，u1'(η1)=u1'(ζ1)=0．将其代入到(6)中有

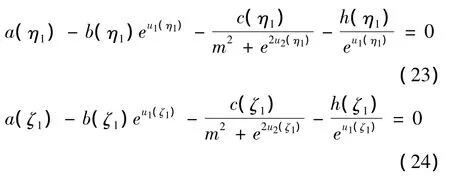
由(23)和(15)可得

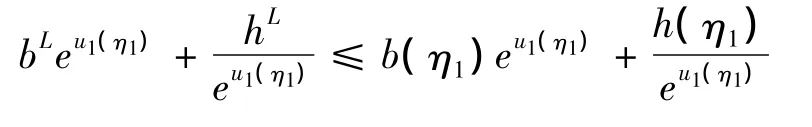
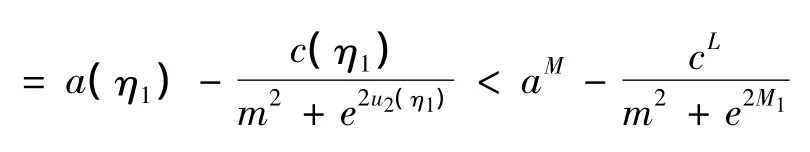
于是解得

类似的，由(25)和(14)可得

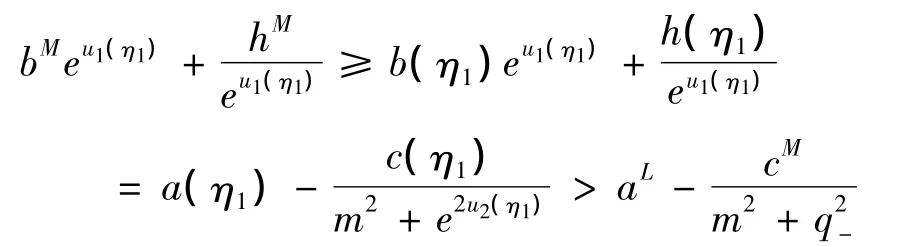
由此可解得

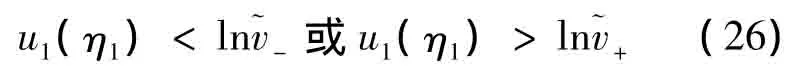
由(17)，(25)知，对 ∀t∈[0，ω]，有

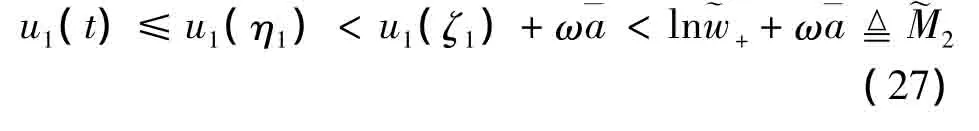
其余部分的证明与定理2．1的相类似，从略．

[1] Xia Y．，Han M．，Multiple Periodic Solution of a Ratio－ dependent Predator － prey Model[J]．Chao．Soli．Frac．，39(2009)1100－1108．

[2] D．Hu，Z．Zhang，Four Positive Periodic Solutions of a Discrete time Delayed Predator－prey System with Nonmonotonic Functional Response and Harvesting， Comput． Math． Appl，56(2008)3015－3022．

[3] Saito Y．，Permanence and Global Stability for General Lotka－Volterra Predator Prey Systems with Distributed Delays[J]．Nonlinear Anal．，47(2001)6157 －6168．

[4] M．Bohner，M．Fan，J．M．Zhang，Periodicity of Scalar Dynamic Equations and Applications to Population Models，J．Math．Anal．Appl．7(5)(2006)1193 －1204．

[5] Wang Q．，Dai B．，Chen M．，Multiple Periodic Solutions of Animpulsive Predator－prey Model with Holling－type IV Functional Response，Math．Comput．Modelling 49(2009)1829 －1836．

[6] R．E．Gaines and J．L．Mawhin．，Coincidence Degree and Nonlinear Differential Equations[M]．Berlin:Springer－ Verlag，1977，40 －60．