考虑商业热点影响的交通流元胞模拟

薛 海，董明家，王 宇，刘文静

(华北水利水电学院，河南 郑州 450011)

考虑商业热点影响的交通流元胞模拟

薛 海，董明家，王 宇，刘文静

(华北水利水电学院，河南 郑州 450011)

在对车辆个体行为研究的基础上，针对城市商业热点对交通流的导向性影响，引入商业热点吸引子的概念并合理概化其作用模式，利用元胞模拟这一非线性过程研究工具，对具有双向通路的准二维交通流进行了初步建模及模拟计算.计算结果表明，商业热点吸引子的引入以及基于元胞方法的交通流模拟可以反映出较为复杂的城市交通基本特征，是交通流模拟的有效研究手段.

商业热点;交通流;元胞方法

随着城市化进程的加快和普通公民收入的持续增加，机动车辆已经成为很多家庭日常代步的首选工具.然而由于相应的城市道路规划、布局和建设的相对滞后，交通拥堵逐渐成为阻碍城市可持续发展的顽症之一.现阶段，对于交通的研究主要包括交通宏观容量的研究、交通实时监控和策略研究等.作为这些研究的基础，首先应该充分认识在各种交通密度及控制措施(如红绿灯控制)下所形成的交通流的规律性，并对其进行较为准确的预测.

Kerner［1］较早指出交通流具有自由流、大范围移动阻塞、同步流等特征，而这些特征叠所呈现出较强的非线性特性，很难用传统方法进行研究.作为一种特殊的动力学建模方法，元胞模型将动力学过程放置在离散网格上，将连续过程离散化，同时又着眼于局部动力学行为(规则)的构造，进而将局部动力学行为叠加并扩散到整个研究域中，这与交通流中车辆个体的起动、行使、刹车等局部行为及不同车辆之间通过局部相互影响并最终将这种影响扩散到整个交通网络中的模式是极为相近的.

实际的城市交通大部分是一个二维网络，有些是三维网络，如立交桥.在这一网络中又有单(双)车道、单(双)行道、红绿灯、交通管制等多种运行模式或制约因素，同时还存在社区及商场群(即商业热点)所产生的交通导向作用等，因此交通流是一个非常复杂的非线性系统.在Cremer和Ludwig［2］首次提出利用元胞方法进行交通模拟后，Nagel和Schreckenberg［3］又进一步提出了 NaSch 模型.这一模型将交通流概化为一维格点模型，并将加速、减速、慢化等行为简化为元胞作用规则以实现交通流模拟.除此之外，B Chopard［4］，Debashish 等［5］又相继提出了不同的二维元胞交通流模型.笔者以Na-Sch模型为基础，将该一维模型扩展为准二维模型(这里的准二维是指在两个方向上仍利用一维模型构造)，在交叉点处设置虚拟红绿灯规则、车辆等待和转弯规则，并重点讨论了引入商业热点吸引子来构建更为接近现实情形的交通流元胞模拟方案.

1 准二维交通流模型规则

1.1 模型布局及基本思路

首先对行车状况进行简化.将道路设置为双行道(禁止调头).为简单起见，车辆在运行过程中暂不考虑横向并道情形，仅在交叉口进行直行或左右拐弯判断.道路本身可看作一系列元胞，元胞状态即为道路上某位置的状态(具有0，1两种状态:0代表该元胞位置上没有车辆;1则代表有车辆).

该模型交通流的片段概化图(接近路口处，其余区域未画出)如图1所示.图1中的方格即为元胞空间.按照实际交通沿右侧行驶的规则.在前方无车的情况下，车辆可以有直行和右转两种选择，此选择随机给定.

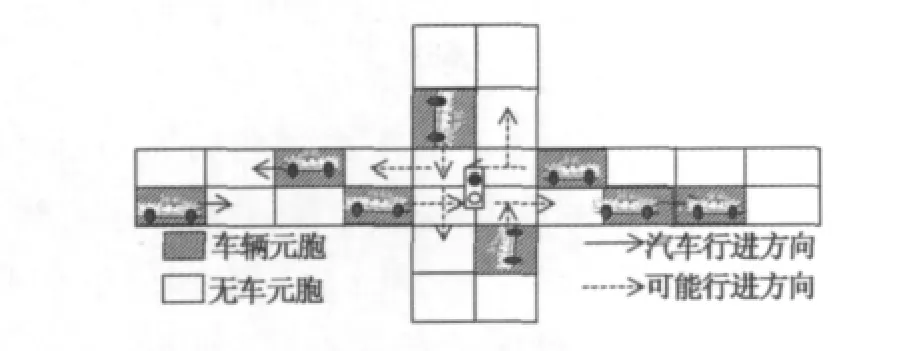
图1 有交叉口的双车双行道交通流路图

定义本模型中的一些基本参数及变量:vi，t为第i辆车在t时刻的行进速度;vi，max为第i辆车可能的最大行进速度(主要考虑到不同车辆的最高性能有所差异);disti，j为第i辆车与其前方的第j辆车之间的距离，即后方车辆的允许行驶距离;Δt为计算域中的元胞更新时间间隔;Δtcollide为碰撞事故处理时间，根据实际经验可设定为10～15 min之间的随机数.

1.2 交通流元胞模型规则

以NaSch模型为基础并进行拓展改进，建立该模型的车辆相互作用规则.

1.2.1 车辆加速规则

在实际交通过程中，如果当前元胞中车辆在运动方向上具有若干空余元胞(未被其他车辆占用)，则假定当前元胞中车辆司机具有加速的倾向.在元胞模型中，首先对前方剩余距离进行判断，以决定当前元胞是否加速驶向前方元胞.车辆加速按照如下规则进行，

当司机判断以当前速度并按照模型规定时间步长所行使的距离在与前方车距范围内时，则下一时刻的速度增加，但如果已接近本车辆的最大速度，则以最大速度行驶，不再增加.需要说明的是:这里的最大速度是一个相对有限的值.过高的最大速度设定需要更细的元胞空间网格和时间间隔，但计算量将显著增加.

1.2.2 车辆减速规则

当遇到前方车距(未被其他车辆占用元胞所代表的距离)小于本元胞车辆当前速度在一个时间间隔中的行驶距离，或者红绿灯元胞处于红灯状态时，为避免和前方车辆产生碰撞，则应该做减速操作.

在NaSch模型中，制定的减速规则为

在此规则中，实际上是首先判断和前方最近的被占用元胞的距离，如果以现在的速度行驶，在下一时刻大于此距离，则直接减速为该距离所对应的速度，否则仍然以当前速度行驶.仔细分析可以发现，该规则描述减速是没有问题的，但这种减速方式在理论上是不可能产生碰撞的.而现实的交通流中，由于车辆碰撞而导致的堵车有时是相当严重的.因此在该模型中做如下改进.

根据实际交通流调查得到的车辆事故率(概率Pcollide)来决定减速规则.如果当前进入交通元胞区域内有n辆车，在程序中按照n*Pcollide个不按式(2)减速规则进行减速操作的车辆将产生碰撞事故(为简化计算，不考虑异向车辆产生的对头碰撞，仅考虑同向追尾碰撞).

1.2.3 碰撞事故拥堵规则

在上述车辆减速规则中按照概率Pcollide产生碰撞交通事故，而交通事故在交通流中最重要的效应就是造成随机的临时堵车.该模型中做如下考虑.

假设在标号为xk及xk+1的元胞位置出现了碰撞事故，则将xk及xk+1元胞标记为1(即占用)，且在之后的 Δtcollide时间之内保持 1状态;在经过Δtcollide时间之后将事故发生元胞状态置为0，表示已经处理完毕，可以通车.而对于xk元胞后方元胞中的车辆，应满足

该规则的含义为:对后方xk处的元胞，若前方出现碰撞事故，则根据相对距离判断，实行相应的减速操作.若已与碰撞发生所在元胞毗邻，则等待Δtcollide后，按原行进规则运行.

1.2.4 红绿灯规则

红绿灯规则与碰撞事故拥堵规则基本一致，其实质均是将所在位置元胞置为已被车辆占用(并未实际被占用，而是仅对某一方向而言).不同之处有两点:一是红绿灯规则中的Δtstop(类似于碰撞事故规则中的Δtcollide)是一个相对较小的值;二是红绿灯在两个方向上具有互逆性，即一个方向为占用时，另一方向元胞设置为0，即保持可流通状态.为简单起见，没有考虑时间较短的黄灯作用.

1.2.5 交叉口行驶规则

实际上，上述红绿灯规则本身就是交叉口规则的一部分.这里主要说明车辆在路口的元胞规则.

与实际交通流相一致，本规则中路口元胞车辆也遵循沿右侧进行直行、右拐等行驶方式.以图1中标有路口车辆和路口元胞的单元为例，路口车辆在下一时刻需进行如下判断及动作.

1)以1/2的概率决定:直行、右转2种选择.

2)如果选择右转，则进一步根据加速规则对右侧车道进行判断.如果有空余元胞，则在下一时刻向右前移.

3)如果选择了直行，则进一步根据红绿灯规则判断路口前方元胞是否为禁止状态(即元胞状态为1).如果为可行驶状态，则在下一时刻向相应方向元胞移动.

该规则中，直行及右转两种选择在实际交通流中也是存在的.在模拟程序中，根据随机数以1/2的等概率来确定两者之一.为简便起见，暂不考虑左转情形.

1.2.6 商业热点元胞吸引子及其作用规则

为模拟城市商业区热点地带对交通的影响，提出交通元胞吸引子的概念.商业热点元胞吸引子，是指存在某一元胞(以其横纵坐标定位)使某一距离内的车辆元胞以一定的概率具有驶向该元胞的倾向，对应于现实中的车辆倾向于驶向城市商业区进行购物的行为.这一行为在现实生活中已经成为交通拥堵的主要原因之一.

该规则的设置思路是:首先对所有元胞中距各商业区吸引子一定范围内的元胞进行元胞属性标记，给出对应于这一元胞的吸引子范围.如果不在任何吸引子范围内，则置为(0，0).在进行每次迭代计算时，如果具有这些标记的元胞被车辆占据，则以事先给定的吸引概率Pattr迫使车辆向商业热点吸引子所在位置演化，而当车辆在吸引子元胞附近的等待和碰撞则按照前述各规则进行(若Pattr=1/200，即表示200个进入吸引子范围的车辆中，有1辆产生驶向吸引子所在元胞的倾向).

设第m个吸引子的元胞坐标为(i，j)，任意普通道路元胞的坐标为(i1，j1)，则

式中:r为吸引子作用域大小，初定为计算域1/5的元胞数量;attr_pos为普通元胞中的吸引子位置属性，用于存储其所在吸引子范围.如果同时位于两个吸引子范围，则以选择dist较小的吸引子位置.

车辆在当前元胞中，首先检查当前元胞的attr_pos值，判断其所在元胞是否位于某个吸引子作用域中.如果确实位于某个吸引子作用域中，那么按式(5)进一步判断，以决定下一步移动到哪个元胞当中(只有在交叉口元胞位置才做下列移动，相当于调头行驶且暂时允许左转，正常元胞空间中即使满足对attr_pos的判断也不按下列规则操作，即禁止随意位置进行反向行驶).

式中:vk，t+1，wk，t+1分别为第 k 个车辆元胞 t+1 时刻在水平车道及竖直车道上的速度;sgn为符号函数.式(5)的直观意义对应于:如果t时刻车辆位于水平车道，则判断其x坐标编号与所在区域吸引子的x位置之间的差异.例如xk位于吸引子水平坐标i的右侧，则sgn(i－xk)=－1，这时车辆k应沿负方向进行移动，从而产生在水平方向趋近吸引子的趋势，竖直方向同理.

需要说明的是，并非对所有位于吸引子作用域的车辆都进行此判断和操作，而仅仅对由随机数概率Pattr决定的车辆进行此项操作.

2 交通流元胞模拟结果及分析

设置元胞空间为50×50的方格.道路均按理想状况布设为正交(不考虑实际交通中的倾斜穿插道路).经数值试验，吸引概率和碰撞概率的值对于交通流演变速度和最终车辆元胞密度有影响，但总趋势是一致的.篇幅所限，这里仅给出碰撞概率Pcollide=1/1 500及商业热点吸引概率Pattr=1/500的情形.元胞空间、商业热点吸引子位置布设、3个不同迭代时间中元胞空间的交通分布的演化结果如图3所示(黑圆点为吸引子所在位置，实际位置不在空白街区，而在距其最近的道路上，放置在空白街区是为避免误认为道路不连贯，因为吸引子元胞本身是通车的，特殊之处只是具有吸引效应).

由图2可知:交通流元胞模拟方法可以初步地、半定量地反映出交通流演化过程.迭代次数为100时(图2(a))，由于进入模拟区域的车辆有限，车辆基本都按照加速规则在进行演化，车辆之间的相互影响基本上还未出现，碰撞事故拥堵规则虽然已起作用(图中黑色框部分)，但并未出现由此引发的局部拥堵，因此总体上呈现出较为流畅的交通流特点.

迭代次数为2 600时.图2(b)中已经明显反映出多种规则综合作用的结果.特别是在多个交叉路口出现了若干相邻元胞被车辆占用的情况.同时在一些非交叉口也出现了局部拥堵现象.此外在总体分布上也可以看出车辆元胞总数随着迭代次数的增加而出现激增的情况.

图2 不同时段交通流元胞模拟结果

迭代次数为5 000时(图2(c))，商业热点吸引子规则的效应初步显现(图中3个黑框区域).在靠近商业热点区域附近，已出现了最多连续9个元胞均为车辆占用元胞的情况(这其中也存在与商业热点附近交叉口的红绿灯规则进行叠加的原因).

3 结语

交通流的模拟是解决城市道路交通拥堵的重要研究手段之一.由于交通流的非线性特征，很难得出其所遵循的确定性的数学物理方程.而目前较好的解决方式是利用元胞模拟这类非线性研究方法模拟其宏观效应.笔者在前人研究基础上，通过建立车辆行驶规则，特别是引入了商业热点吸引子概念和规则实现了这一过程的模拟.计算表明，模型可以更好地反映由于商业网点的存在而额外造成的交通拥堵情形，可以为考虑交通影响下的商业网点的合理布设规划提供理论依据.

［1］Kerner B S.Three-phase traffic theory and highway capacity［J］.Physica A，2004，333:379 －440.

［2］Cremer M，Ludwig J.A fast simulation model for traffic flow on the basis of Boolean operations［J］.J Math Comp Simul(S0378 －4754)，1986，28(4):297 －303.

［3］Nagel K，Schreckenberg M.A Cellular automaton model for freeway traffic［J］.J Phys I(France)，1992，2:2221－2229.

［4］Chopard B，Luthi P O，Queloz P-A.Cellular automata model of car traffic in two-dimensional street networks［J］.J Phys A，29:2325-2336，1996.

［5］Debashish Chowdhury，Dietrich E Wolf.Practical hopping models for two-lane traffic with two kinds of vehicles:Effects of lane-changing rules［J］.Physica A(S0378 －4371)，1997，235(3):417 －439.

Cellular Automata Simulation of Traffic Flow Considering the Influence of Commercial Hotspots

XUE Hai，DONG Ming-jia，WANG Yu，LIU Wen-jing
(North China Institute of Water Conservancy and Hydroelectric Power，Zhengzhou 450011，China)

Based on the study of individual vehicle motion，the focus is put on the guiding influence caused by commercial hotspots and a concept named commercial hotspots attractor is introduced.By using the cellular automata method which is a nonlinear math tool，the calculation is carried out to simulate the quasi-2D and bi-directional traffic flow.The results show that the cellular automata method introducing the commercial hotspots attractor is an effective solution to simulate more complex urban traffic features.

commercial hotspots;traffic flow;cellular automata method

1002－5634(2012)03－0016－04

2012－03－09

河南省高等学校青年骨干教师资助(2010GGJS－124);华北水利水电学院高层次人才科研启动项目资助(200805).

薛 海(1974—)，男，河南修武人，副教授，博士，主要从事流域水沙运动及其非线性特征方面的研究.

(责任编辑:陈海涛)