基于Alpha-NMF的AD样本分类及特异性基因选择方法
卢晓丽,孔 薇
(上海海事大学 信息工程学院,上海 201306)
阿尔茨海默病(Alzheimer disease,AD)是德国神经病学家Alois Alzheimer于1907年首次对一位51岁的病人描述的,至今对AD的认识和研究已经进行了100余年了。它是老年人中最常见的神经退行性疾病之一,其临床特点是隐袭起病,逐渐出现记忆力减退、认知功能障碍、行为异常和社交障碍。65岁以上老年痴呆人群中超过55%的病例是阿尔茨海默病[1]。随着全球人口的老龄化,痴呆患病人数大量增加,阿尔茨海默病已经成为人类共同面临的严峻挑战。
DNA微阵列技术[2]能够对大量的基因进行同步、快速测量,同时提供成千上万条基因的表达水平,使得生物学家能够在基因组层次上研究任何种类细胞在任意给定时间、任意给定条件下的基因表达模式。由于基因表达谱数据的高噪声、高维性、高冗余以及数据分布不均匀等特点使得在分析过程中仍然有很多挑战性问题。
非负矩阵分解 (non-negative matrix factorization,NMF)方法[3]由Lee和Seung在一篇关于无监督学习的文章中提出的一种新的矩阵分解方法。该方法在矩阵分解过程中对矩阵元素进行非负约束,在实际应用中具有明确的物理意义。相比一些传统的算法,NMF具有实现简便,分解形式和分解结果可解释性强等诸多优点。NMF算法被提出后,随着研究的不断深入,为了适应不同领域的需求,一些研究者设计了基于多种目标函数的算法对标准NMF算法进行改进。目前,应用比较频繁的有稀疏非负矩阵分解 (sparse non-negative matrix factorization,SNMF)、非平滑非负矩阵分解(non-smooth non-negative matrix factorization,NSNMF)以及加权非负矩阵分解 (weighted non-negative matrix factorization,WNMF) 等。NMF已逐渐应用于语音信号处理、模式识别、图像分析等研究领域中,并且获得了很好的效果。相信不久的将来,NMF能够适应于更多领域的需求。
1 非负矩阵分解算法原理
NMF理论上是利用非负约束条件来获取数据表示的一种方法。NMF问题可以描述为:已知非负矩阵Vn×m,找到一个非负矩阵 Wn×r和 Hr×m一个非负矩阵,使得:

此时矩阵V中的列向量可以近似地看作是非负矩阵W的列向量的非负线性组合,组合系数为hj的分量。因此矩阵W=(w1,…,wr)可以看成是对V进行线性估计的一组基,而H则是V在基W上的非负投影系数。
1.1 基本NMF算法
根据NMF理论的数学模型,必须找到一个分解过程V≈WH,使得WH尽量逼近V,可以定义一个目标函数来保证逼近的效果。目标函数可以利用某些距离的测量来获得,通常使用的目标函数是欧式距离,即:
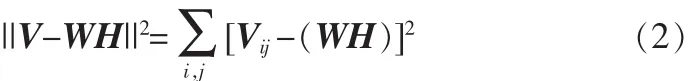
当且仅当V=WH时取最小值为0。因此NMF问题可以转化为优化问题用迭代方法交替求解W和H。虽然式(2)对于单独的W和H来讲均是凸函数,但是同时对于W和H却不是凸函数,因此找到一个全局最优解是不太现实的,但可以寻找一个局部最优解。NMF算法可以定义为如下优化问题:最小化||V-WH||2,交替更新W,H。最简单易行的更新方法就是梯度下降法,但是其收敛速度非常缓慢。更新规则如下:
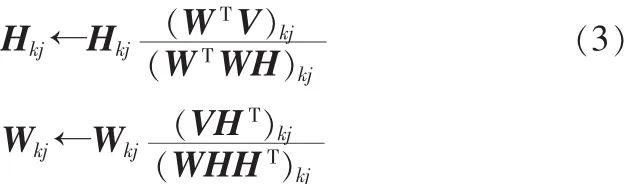
定理1:在(3)迭代规则下,欧式距离||V-WH||2是单调不增的,如果当W和H的值是固定的,||V-WH||2保持不变。
1.2 Alpha-NMF算法
Alpha-NMF算法[4]是NMF算法的一种改进,它是针对信号处理所提出的一种新的算法。
Alpha-NMF算法的数学模型为:
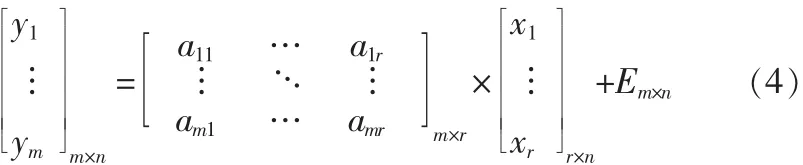
Y=[y1… ym]T=V为m个非负的n维观测信号,A=HT为m×r维的非负的混合矩阵,X=[x1,…,xr]T=WT为r个非负的n维源信号,E为噪音。
Alpha-NMF算法的目标函数为:
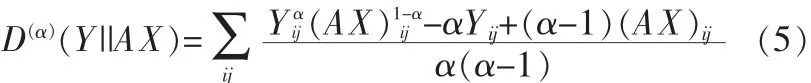
A、X迭代规则如下:
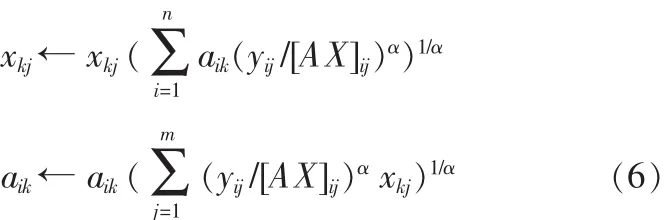
根据α取值不同,可以得到Pearson偏差、Hellinger偏差和 Neyman’s chi-square 偏差,其 α 分别为 2,0.5,-1。
2 非负矩阵分解在基因表达谱数据中的应用
2.1 数据预处理
文中所选的实验数据为基因表达综合数据库[5](GEO)中23组大脑海马区域(HIP)和23组内嗅区皮质(EC)的AD样本,54 675个基因表达数据;其中海马区域的基因数据集由13个control AD样本和10个affected AD样本组成,内鼻皮质区域的基因数据集由13个control AD样本和10个affected AD样本组成。由于基因表达谱数据的复杂性,在进行聚类分析前必须先进行预处理和数据转换等过程。本文先采用小波变换[6](wavelet transform,WT)方法对数据进行降噪,然后通过微阵列显著性分析[7](significanceanalysisofmicroarrays,SAM)工具箱筛选出显著变化的上下调基因。
2.2 Alpha-NMF算法应用于基因表达谱数据
Alpha-NMF算法被提出后,至今还设被应用于基因表达数据中,通过大量的实验,证明了Alpha-NMF算法能够有效的应用到该领域中,相比传统NMF算法,其算法稳定性和分类准确率明显较高。
基因表达谱数据的Alpha-NMF混合模型如图1所示。Y表示m×n维基因表达谱数据,每一行表示一个样本集,每一列表示一个基因在不同条件下的表达水平。yij表示第j个基因在条件i下的表达水平,通常nm。
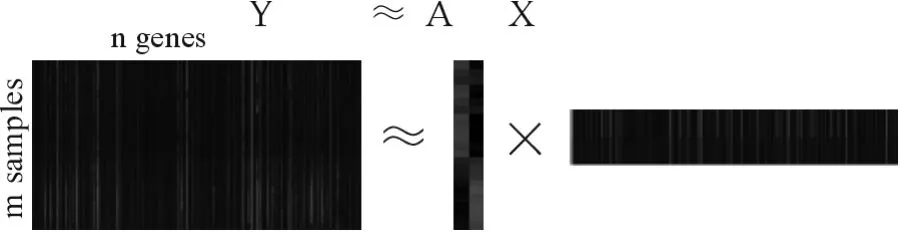
图1 Alpha-NMF混合模型Fig.1 Mixture model of Alpha-NMF
任一样本yi可以表示为:
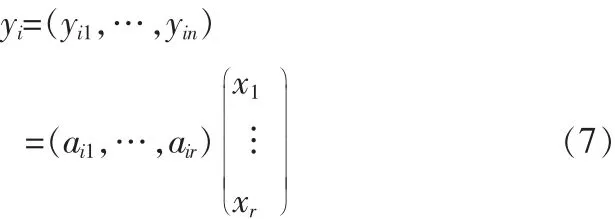
也就是说每一个样本可以近似看做是非负矩阵X的行向量的非负线性组合,组合系数是矩阵A对应行向量的分量。把分解后的矩阵X的每一行称为一个集合基因。矩阵A的第k列为X的第k个集合基因的系数,若矩阵X能表征原始数据的局部特征,则系数矩阵A与样本类别紧密相关,即类别c1对于特征k的贡献大,而c2对于特征k的贡献小。对于每一个集合基因(图2为HIP数据经Alpha-NMF算法,α=0.5时分解后相关系数为0.97集合基因的柱状图),若元素的值相对较大,说明其对应的基因j与AD紧密相关。
3 实验结果与分析
首先采用WT-SAM方法分别对HIP和EC数据进行预处理,筛选后的基因数分别为13 587个、6 567个,再对数据进行非负化处理,然后通过Alpha-NMF算法进行分解,利用分解后的A矩阵进行聚类,本文采用k均值聚类方法对A的行向量进行聚类,得到一聚类结果。对于矩阵X,设定一阈值,筛选出集合基因中大于该阈值的信息基因。
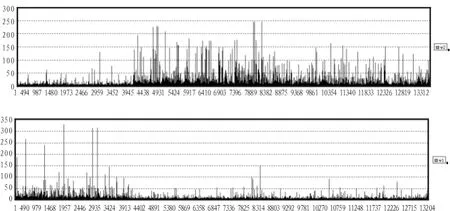
图2 两个集合基因的柱状图Fig.2 Histogram of factor1 and factor2
由于NMF算法受初值和维数r的影响,因此对每组实验分别取r=2,3,4,5时运行NMF算法 20次。为了衡量由于r值选取不同导致的聚类的稳定性问题,定义了一个共表型相关系数[8](图3分类稳定性比较),共表型相关系数越接近于1,分类越稳定。
观察图3和图4的结果,通过比较可以发现,随着r的增加,其相关系数和分类正确率普遍降低,当r=2时,其分类稳定性和识别正确率明显高于 r=3,4,5时的情况。此时,Alpha-NMF算法相比标准NMF算法具有较高的分类准确性和稳定性。尤其当α=0.5时,效果最佳。因此,选择Alpha-NMF算法α=0.5,r=2处理后的集合基因,如图2所示,选择某一阈值 (此处阈值为50),可以分别提炼出268个(HIP)、172(EC)个探针表达变化具有显著差异。
4 讨 论
4.1 特异性基因及其功能分类
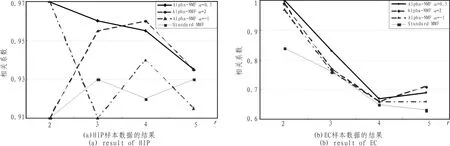
图3 分类稳定性Fig.3 Classification stability
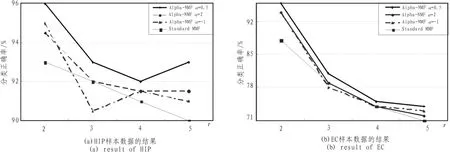
图4 识别准确率Fig.4 Identification accuracy
将上节提炼出的探针号与AD基因组进行比对,共确定有320个基因为特异性基因。这些基因主要于细胞信号传导、物质代谢、物质传输等生物过程有关。
MiMI(Michigan Molecular Interactions)[9]是国家卫生研究所疾病预防控制综合生物情报中心中的一部分。它可以提供蛋白质间的相互作用,并且利用这些数据进行融合,集合成一个复杂的网络;还能检索大量基因的生物功能。
使用MiMI对上上述特异性基因进行功能分类,其中有88基因在GO(Gene Ontology)[6]上没有注释,因此没有对其分类,仅对其余的232个基因进行分类,根据分类结果,主要分为以下几类:1)物质代谢过程,包括蛋白质代谢、细胞氮化合物代谢、核苷酸代谢;2)细胞周期过程,包括细胞形态发生和发展、细胞自动调节机能、生殖细胞形成;3)定位过程,包括蛋白质定位、细胞定位、大分子定位;4)细胞成分组织,包括细胞内大分子聚集、细胞膜组织以及细胞内各器官组织;5)生物合成过程,包括核苷酸合成、小分子合成;6)基因表达、转录、翻译;7)神经系统调节,包括神经元的形成、神经突触传导、神经元变异、神经传导素生成及传输;8)细胞凋亡;9)物质运输,包括ATP水解耦合质子运输、阳离子运输、胞内蛋白质运输、离子跨膜运输。上述基因功能分类如表1所示。

表1 特异性基因功能分类Tab.1 Functional classification of specific genes
4.2 利用Cytoscape工具构建基因功能结构图
BiNGO[10]是Cytoscape里的一个插件,它让Cytoscape链接到Gene Ontology,使每个基因赋予注释,构建基于目的的基因功能的结构图。
将232个特异性基因提交给BiNGO,输出一幅包含123个节点和165条边的结构图,基因功能结构图中每个节点表示一个生物过程,每一条边表示生物功能间的关系。其中节点的大小表示与该过程相关的基因占232个信息基因的比例,点的颜色与p-value相关,颜色越深表示p-value越大,也就是说该节点显著过表达。如图5所示,可以发现,提取的232个基因主要在细胞周期过程、定位过程及传输过程等生物过程上显著过表达;在生物合成、代谢过程和一些与神经系统相关的生物过程也有一定程度的显著过表达。这些特异性基因有的与Aβ的聚集有关,有的与神经递质的传输有关或与神经元的形成发展有关,还有的与金属的代谢相关,它们都能伴随着细胞的炎症反应,导致神经元损害,引起记忆减退和认知障碍,产生痴呆症状。来的特异性基因具有显著差异表达,并且它能提炼出目前确定与AD致病相关的基因(APP)。通过构建基因功能结构图,加深了对生物过程的理解,从而为生物学实验的验证提供的明确的方向。
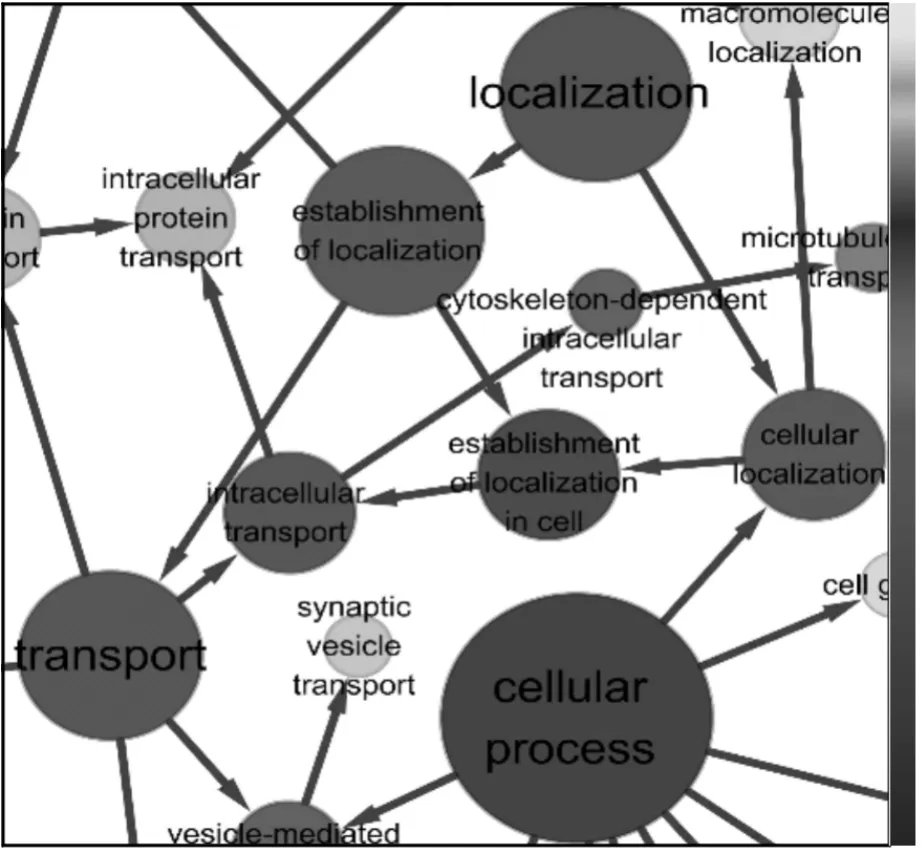
图5 特异性基因功能结构图Fig.5 Functional structure map of metagenes
5 结 论
通过以上的实验和阐述可以看出,Alpha-NMF算法较传统NMF算法具有较高的分类准确性和稳定性,算法的运算速度也有较大的提高。由Alpha-NMF算法处理后所提炼出
[1]Strobel G.A virtual toast to thal,nitsch,and stanley on their awards[J].Alzheimer Research Forum,2004.
[2]Schachtner R,Lutter D,Theis F J,et al.How to extract marker genes from microarray data sets[J].IEEE Engineering in Medicine and Biology Society,2007(1):4215-4218.
[3]Lee D,Seung H S.Unsupervised learning by convex and conic coding[J].Advances in Neural Information Processing Systems,1997(9):515-522.
[4]Cichocki A,Amari S,Zdunek R,et al.Extended SMART algorithms for non-negative matrix factorization [C]//8th International Conference on Artificial Intelligence and Soft Computing,Poland,2006,25-29.
[5]Barret T,Troup D B,Wilhite S E,et al.NCBI GEO: archive for high-throughput functional genomic data [J].Nucleic Acids Res,2008(37):885-890.
[6]Abramovich F,Baukey T,Sapatinas T.Wavelet analysis and its statistical application[J].JRSSD,2000(48):1-30.
[7]Efron B,Tibshirani R.Microarrays, empirical bayes methods,and false discovery rates[J].Gen.Epi,2002(1):70-86.
[8]Brunet J P,Tamayo P.Mesirov metagenes and molecular pattern discovery using matrix factorization[J].Proc Natl Acad Sci U S A,2004,101(12):4164-4169.
[9]Tarcea V G, Weymouth T,Ade A,et al.Michigan molecular interactions:from interacting proteins to pathways[J].Nucleic Acids Research,2008:D642-D646.
[10]Maere S,Heymans K,Kuiper M.BiNGO: a cytoscape plugin to assess overrepresentation of Gene Ontology categories in biological networks[J].Bioinformatics,2005:3448-3449.

