基于CORDIC算法的数字下变频技术设计与实现

侯武威，袁安民，赵颖辉

（空军工程大学 电讯工程学院，陕西 西安710077）

传统的数字下变频器（DDC）是将本地数控振荡器（NCO）产生的信号与输入信号相乘实现数字下变频。NCO产生离散正弦信号最简单、最直接的方法就是查表法（LUT），即事先根据各个NCO正弦波相位计算好相应的正弦值，并按相位角度作为地址存储该相位的正弦值数据[1]。

1 NCO结构

图1为用查表法实现的NCO结构，DDC工作时，每向DDC输入一个待下变频的信号采样样本，NCO就增加一个相位增量，然后按照相位累加角度作为地址，检查该地址上的数值并输出到数字混频器，与信号样本相乘，完成数字下变频。其中，初始相位控制字用来设置本振信号的初相，相位步进控制字用来设置本振信号的频率。

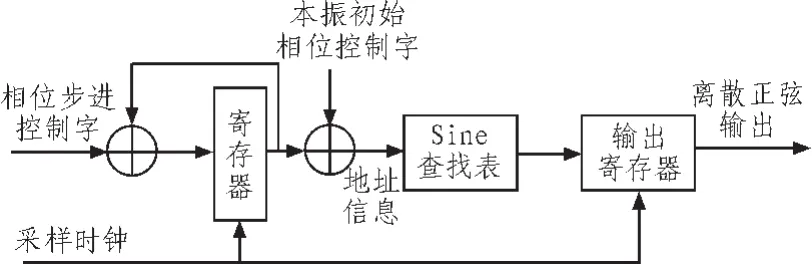
图1 查表法NCO基本结构Fig.1 Basic diagram of look-up table method NCO

2 CORDIC算法基本原理

CORDIC算法是由J.Volder等人在1959年首先提出的[2]，该算法通过迭代方式仅用加法和移位2种运算进行矢量旋转，不仅可以用来计算正余弦、极坐标和直角坐标变换与反变换、反正切、矢量求模，而且还可以实现反正弦和反余弦函数的计算，摆脱了用查表法产生离散正弦信号需要占用大量ROM资源的弊端。CORDIC算法由于只采用加法和移位运算，很适合在FPGA中实现，可以用来实现数字下变频功能。

设一向量（x′1，y′1），旋转 θ角后得新向量（x′2，y′2），如图 2所示，根据坐标变换规则，两者有如下关系：

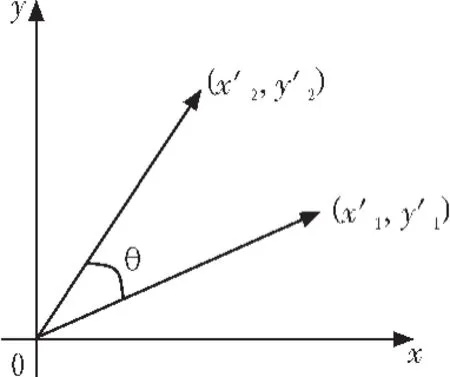
图2 CORDIC算法原理图Fig.2 Principle block diagram of CORDIC algorithm

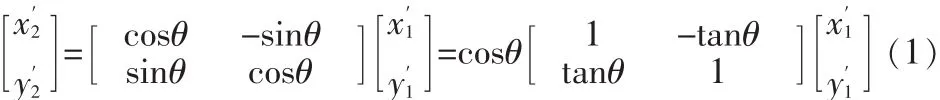
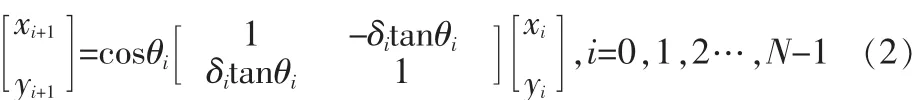
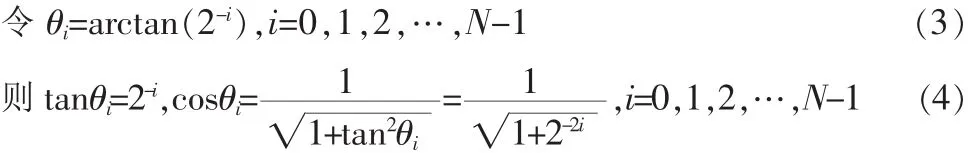
式（2）可改写为：

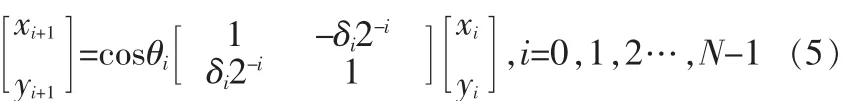
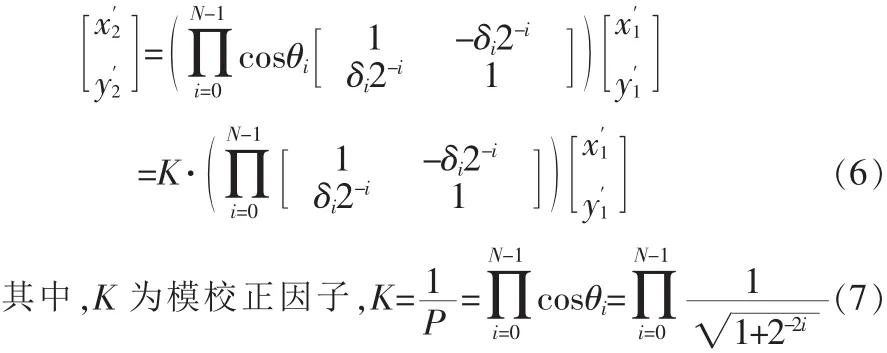
当 N→∞ 时，有 zi+1=zi-δiarctan（2-i），i=0,1,2,…，N-1，θ，故K可以看做一个常数。

这样，向量旋转式（1）的计算问题转换为式（7）的计算以及如下迭代运算。

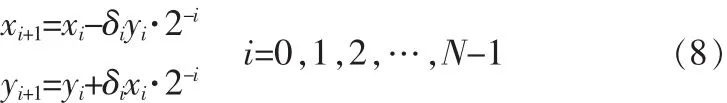
式（8）中仅含移位、加减法算法，特别适合硬件实现，为硬件快速计算三角函数提供了一种新的算法，这就是提出CORDIC算法的初衷。迭代计算时，为了跟踪已经旋转的角度，还需引入一个新变量，定义为：

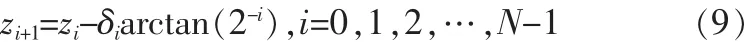
表示第i次旋转后剩余未旋转角度。上式中arctan（2-i）可以预先求出，保存在寄存器中。式（8）与式（9）构成了CORDIC算法的基本迭代关系。

为了能计算更多的基本函数，1971年，J.S.Walther提出了统一的CORDIC算法，引入参数m表示工作模式：m=1为圆周系统、m=0为线性系统、m=-1为双曲系统，将3种系统统一到同一个CORDIC迭代方程中，表示为：

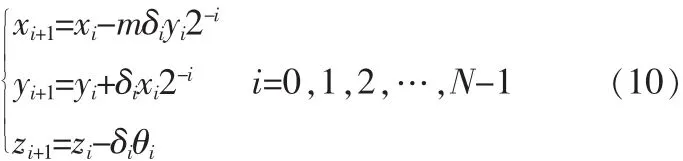
3 基于CORDIC算法的NCO及混频器设计

为了提高数控振荡器的频率分辨率，往往需要扩大存储器的容量，造成存储资源的大量消耗。因此，当设计高速、高精度的数控振荡器时，查表法就不合适采用。因此，可以考虑利用算法实时产生正余弦样本，基于矢量旋转的CORDIC算法正好满足这一需求，该算法有线性的收敛域和序列特性，只要迭代次数足够，即可保证结果有足够的精度[3]。

本文应用CORDIC算法圆周旋转模式产生正余弦信号，令 m=1，则 θi=arctan2-i，旋转方向由 zi决定，若 zi>0，则 δi=-1，若zi<0，则δi=+1，经过n次迭代最终使zi趋于0。迭代的最终结果为：

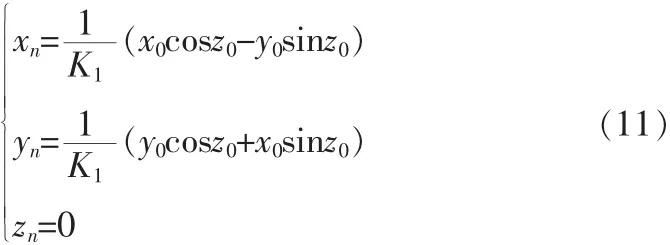
给定相位值，利用CORDIC算法就可以实时产生相对应的正余弦值，在本设计中，NCO产生的正余弦样本要与接收信号 x（n）相乘，通过观察式（9），本文给定初值 x0=x（n），y0=0，z0=φ，则式（9）可化为：

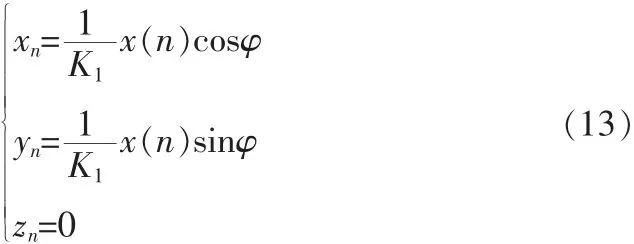
从式（13）可以看出，利用CORDIC算法同时实现了NCO和混频器，既节省了资源，又提高了效率[4]。图3给出了NCO和混频器的实现框图，在时钟的控制下，频率偏移控制字不断调整本地频率控制字，对调整后的频率控制字进行累加，截取输出值的高位与相位偏移控制字相加，每来一个时钟，得到一个相位φ，利用CORDIC算法计算相位φ的正余弦值并与接收信号 x（n）相乘，得到 I（n）和 Q（n），同时实现了 NCO 及混频器。

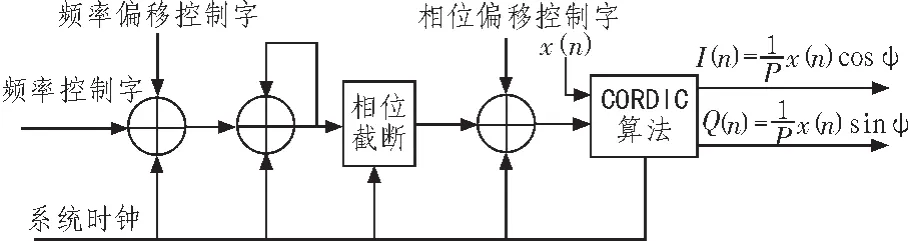
图3 基于CORDIC算法的NCO和混频器实现框图Fig.3 Block diagram of NCO and frequency mixer based on CORDIC algorithm

4 CORDIC算法的FPGA实现

CORDIC迭代算法的一种直接实现方式是反馈结构[5]，此结构只设计一级CORDIC运算迭代单元，然后在系统时钟的驱动下，将本级的输出作为本级的输入，通过同一级迭代完成运算。这种方法硬件开销很小，但控制比较复杂，而且完成一次CORDIC运算需要多个时钟周期，运算速度较慢不利于数据的高速实时处理。

CORDIC迭代算法的另一种实现方式是流水线结构，每一级CORDIC迭代运算都使用单独的一套运算单元，它的处理速度非常快，为数据实现高速实时处理提供了前提[6]。每一级实现的功能是根据式（8）和式（9）进行一次迭代，移位的位数等于当前的迭代级数，加减法选择由该级中z的最高位（符号位）决定，得到下一级的x、y和z的值。经过N级流水线运算后，z的值变为0，x和y的值则为初始值z的余弦和正弦值。可以看出，在迭代过程每一级电路结构中只有移位和加减运算，级与级之间直接相连，不需要额外的寄存器，特别适合于FPGA实现，其结构如图4所示。

5 仿真及其结果分析

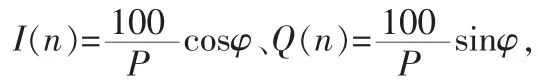
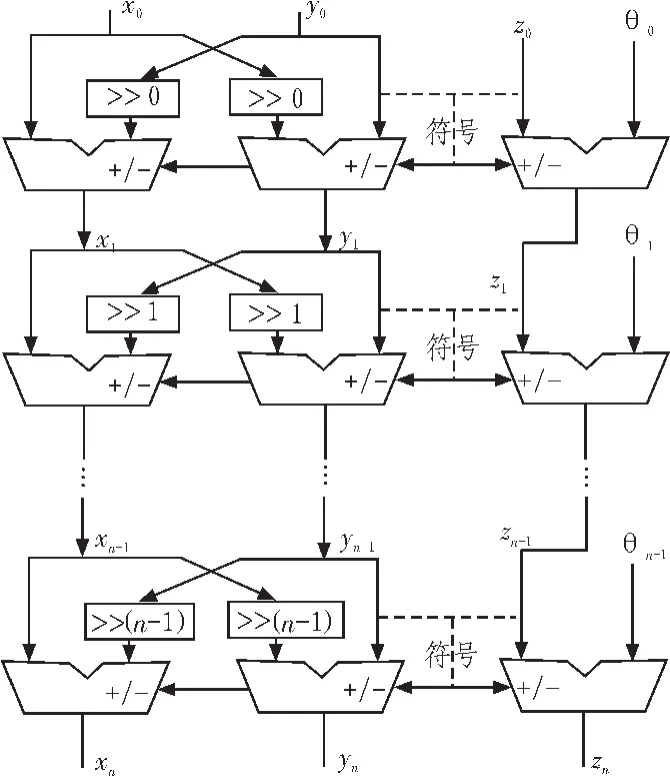
图4 CORDIC算法流水线结构图Fig.4 Structure diagram of CORDIC pipeline implementation

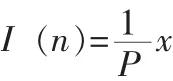
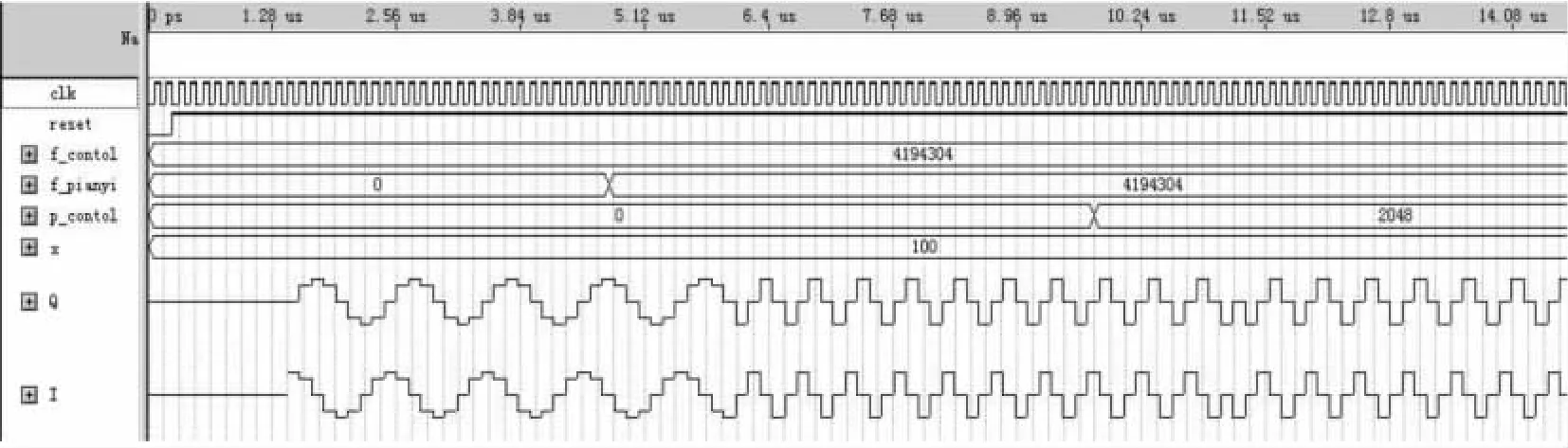
图5 NCO及混频器仿真结果Fig.5 Simulation result of NCO and frequency mixer

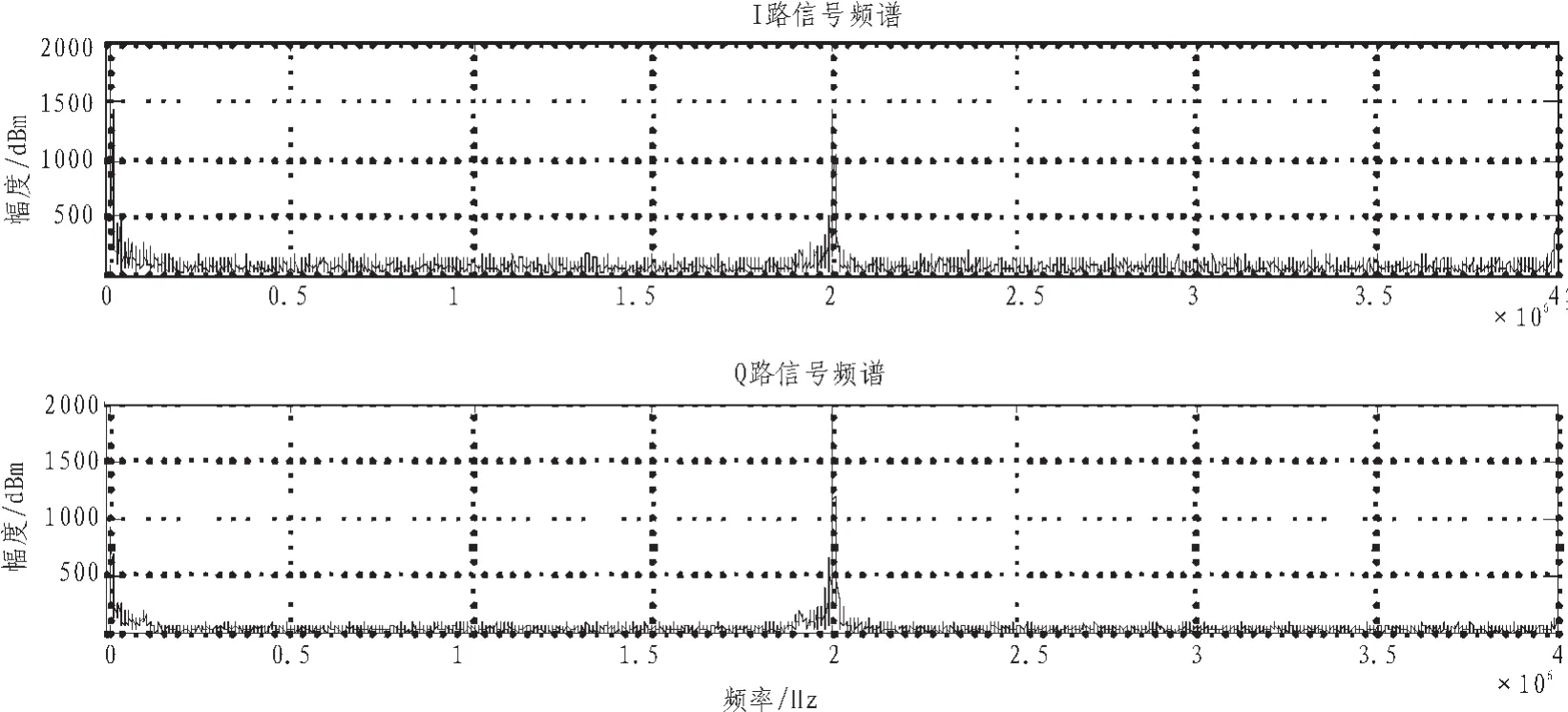
图6 I路信号和Q路信号的频谱Fig.6 Frequency spectrum of I and Q

6 结束语

本文提出了一种基于CORDIC算法的数字下变频方法，克服了传统数字下变频器查询表大的缺点，而且该算法将NCO和混频器合在一起完成，占用资源少，效率高、速度快、精度高，采用流水线结构，只有加法和移位单元，易于FPGA实现，具有较高的工程应用价值。

[1]杨小牛，楼才义.软件无线电原理与应用[M].北京：电子工业出版社，2005.

[2]Volder J E.The CORDIC trigonometric computing technique[J].IRETransactionsonElectronicComputers，1959，8（3）：330-334.

[3]赵林军.基于CORDIC算法的DDC实现[J].微计算机信息，2008，24（10）：274-275.

ZHAO Lin-jun.Theimplementation ofDDC based on CORDIC algorithm[J].Microcomputer Information，2008，24（10）：274-275.

[4]张科峰，彭帅，蔡梦.基于CORDIC算法的NCO[J].现代雷达，2008，30（6）：91-94.

ZHANG Ke-feng，PENG Shuai，CAI Meng.The NCO based on CORDIC algorithm[J].Modern Radar，2008，30（6）：91-94.

[5]骆艳卜，张会生，张斌.一种CORDIC算法的FPGA实现[J].计算机仿真，2009，26（9）：305-307.

LUO Yan-bo，ZHANG Hui-sheng，ZHANG Bin.FPGA implementationofaCORDIC algorithm [J].Computer Simulation，2009，26（9）：305-307.

[6]杨宇，毛志刚，来逢昌.一种改进的流水线CORDIC算法结构[J].微处理机，2006（4）：10-13.

YANG Yu，MAO Zhi-gang，LAI Feng-chang.An improved pipeline structure for CORDIC algorithm[J].Microprocessors，2006（4）：10-13.

[7]王旭东，潘广桢.MATLAB及其在FPGA中的应用[M].北京：国防工业出版社，2006.