基于神经网络的图像识别

王强，张小溪，韩一红

（西北工业大学 陕西 西安 710129）

图像识别作为图像技术的一个分支一直是图像处理和模式识别领域的研究热点。传统的模式识别方法应用于图像识别主要是利用图像的颜色特征、形状特征、纹理特征等对图像进行比较[1-2]，根据这些统计特征对图像之间的相似度做出评价。

人工神经网络[3]（Artificial Neural Network，ANN）的研究虽然自上世纪40年代才开始，但由于具有强大的自适应能力、信息的分布式存储、并行处理以及能很好的模拟非线性系统，已经在信息处理、模式识别等领域得到越来越广泛的应用。在图像识别中常用的神经网络模型[4-5]有Hopfield神经网络、BP神经网络、小波网络、细胞神经网络和模糊神经网络。对于数字图像来说，采用神经网络是一种有效的手段，而MATLAB中包括的神经网络工具箱为相关的算法开发与数据分析提供了非常友好的环境，避开了比较繁杂的子程序编写任务。

文中应用MATLAB 7.1神经网络工具箱设计BP神经网络，利用提取的图像特征对BP神经网络进行训练，从而达到系统自动识别字符图像的目的。

1 数字图像处理

1.1 图像预处理

字符图像预处理的目的是使字符图像更清晰，边缘更明显，并将每一个字符分割出来便于进行特征提取工作。针对本文选取的字符图像，给出图像预处理的一般流程图如图1所示。

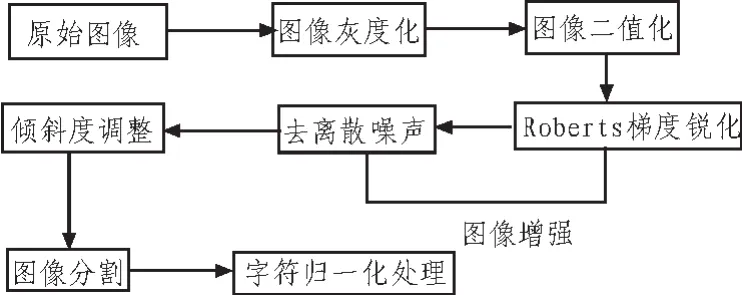
图1 字符图像预处理流程图Fig.1 Flow chart of character image pre-processing

原始字符图像及经过预处理之后的图像如图2、3所示。

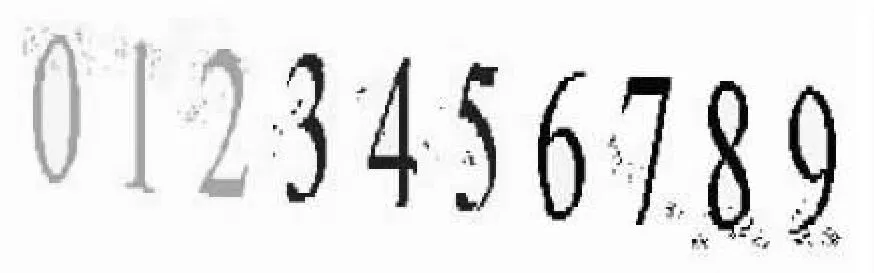
图2 原始字符图像Fig.2 Initial character image

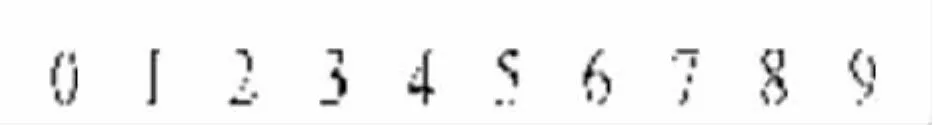
图3 图像预处理之后的字符Fig.3 Character image after pre-processing

经过图像预处理后得到的归一化的结果为每个字符的像素数16×8（16为高度，像素行数；8为宽度，像素列数）大小。

1.2 特征提取

特征提取可以看作是一种特殊的图像数据的简化，其目的是从高维的数据中抽取出有效的包含主要信息的低维数据，便于图像分割和识别。一般来说，良好的特征应该具有可区别性、可靠性、独立性好、数量少这4个特点。传统的特征提取方法基于图像的空频域特征，包括傅里叶变换、小波变换等算法。

针对本文所要识别的图像，对预处理之后得到的图像提取的特征为欧拉数、字符图像矩阵每行的与每列的黑色像素点之和这两个特征。

特征1：欧拉数。欧拉数定义为一个区域中的孔数H和连接部分数C的差：E=C-H。图像的欧拉数是图像的一种拓扑性质度量，它表明了图的连通性。

对数字图像而言，如果图像的背景用“0”标记，目标物体用“1”标记，则欧拉数计算公式如下：

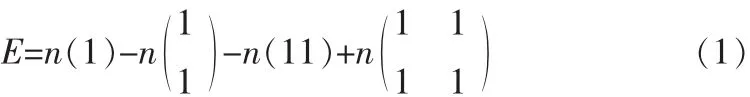
应用MATLAB软件可以用bweuler函数来求图像的欧拉数，调用格式为：

式（2）中，I为输入的二值图像，n设置邻域的大小，即4-邻域或8-邻域，默认值为8。不过必须注意，二值图像的背景为“0”，目标为“1”，检测出的欧拉数才是目标图像的欧拉数。

特征2：字符图像矩阵每行的与每列的黑色像素点之和。这种特征提取方法的算法就是自左向右对经过预处理之后字符图像进行逐列的扫描，统计每列黑色像素的个数，然后自上向下逐行扫描，统计每行的黑色像素的个数，将统计的结果作为字符的特征矩阵。

2 BP神经网络

2.1 BP网络结构及算法

BP（Error Back Propagation Network）神经网络[4，6]是在 1986年由Rumelhant和McClelland提出来的，是目前应用最为广泛和成功的神经网络之一。它是一种多层前馈神经网络，最为普遍的为三层BP网络，所谓三层包括了输入层、输出层和中间层（或称为隐层）。

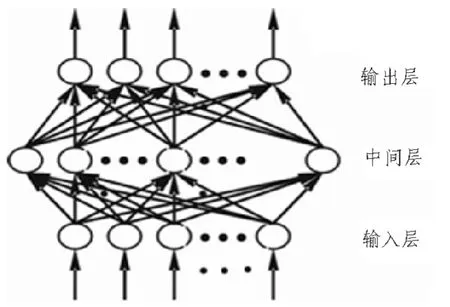
图4 一个典型的BP网络Fig.4 A typical BP network

BP网络结构算法可描述如下：

1）设置变量和参数，其中包括训练样本，权值矩阵，学习速率。

2）初始化，给各个权值矩阵一个较小的随机非零向量。

3）随机输入样本。

4）对输入样本，前向计算BP网络每层神经元的输入信号和输出信号。

5）由期望输出和上一步求得的实际输出计算误差E（n），判断其是否满足要求，若满足则转至第8步，不满足则转至第6步。

6）判断是否大于最大迭代次数，若大于则转至第8步，若不大于，对输入样本方向计算每层神经元的局部梯度δ。

7）根据局部梯度修正各个矩阵的权值。

8）判断是否学完所有的训练样本，是则结束，否则转至第3步。

神经网络应用于图像识别的一般模型如图5所示。

图5 神经网络图像识别框图Fig.5 Model of image recognition based on ANN

2.2 Matlab 7.1神经网络工具箱简介

在设计BP网络时有大量的工作需要进行，而在Matlab 7.1的神经网络工具箱中有对应的函数可完成BP网络设计时所涉及到的全部计算任务。通过应用神经网络工具箱可以较为便捷地完成BP网络的设计。

MATLAB神经网络工具箱中提供的相关函数主要有：BP网络生成函数newff，神经元变换函数，初始化函数init，学习函数，性能函数，训练函数train，BP训练算法函数，仿真函数sim，绘图函数 poltperf。

应用Matlab神经网络工具箱[7]实现BP神经网络的基本步骤如下：

1）网络创建 通过函数newff生成一个BP网络，它会根据样本数据自动确定输入层、输出层的神经元的数目，而隐层的层数、隐层神经元数目、隐层和输出层的变换函数、训练算法函数由用户自己确定；

2）网络初始化 当newff创建网络对象的同时，自动调动函数init根据缺省的参数对网络进行连接权值和阈值的初始化；

3）通过函数train对网络进行训练 对神经网络的训练有2种方式，一种是增加方式，即每输入一个学习样本就根据网络误差进行连接权值和阈值的更新；另一种是批处理方式，即只有全部学习样本都学习完成后，才进行网络连接权值和阈值的更新。函数train采用的是批处理方式，要对其参数进行设置，如学习步长、误差目标等；

4）网络仿真 函数sim根据已训练好的网络对测试数据进行仿真计算。利用此函数，可以在网络训练前后分别进行输入输出的仿真，以作比较，从而对网络进行修改评价。

3 实验仿真

文中采用3层BP网络，具体设计如下：

1）输入层 本文将训练样本图片中提取的字符图像特征：欧拉数与图像矩阵每行的与每列的黑色像素点之和作为BP神经网络的输入p矩阵。输入层节点数为25。

2）输出层 规定：如果网络输入为字符“0”则目标输出t对应列的行元素全为“0.1”，输入为“1”则t对应列的第一行元素为“0.9”，其余行元素全为“0.1”，输入为“2”则对应列的第二行元素为“0.9”，其余行元素为“0.1”，依次类推。输出层节点数为9。

3）隐层 隐层节点数的确定按照下面的经验公式[8]：

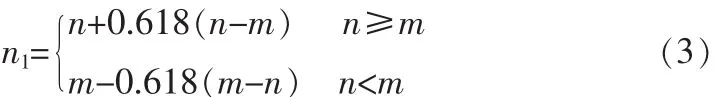
其中，n为输入节点数，m为输出节点数，n1为隐层节点数。计算确定隐层的节点数为35。

确定完BP的三层网络后就可以对网络进行训练，然后用训练好的网络来进行模式分类实现字符图像的识别。图6为网络的训练过程。

仿真结果表明，单个字符的识别率不近相同，最高的为字符8，识别率达95%，最低的为字符2，识别率为75.5%，所有字符平均识别率为89%。

4 结 论

由实验仿真可知，采用神经网络识别图像是切实可行的，由于时间关系，目前只是对普通的BP网络进行了研究应用。下一步的工作是研究BP神经网络的改进算法，并应用改进的BP网络提高图像的识别率以及对复杂图像的识别。

图6 BP网络训练图Fig.6 BP network training chart

[1]齐敏，李大建，郝重阳.模式识别导论[M].北京：清华大学出版社，2009.

[2]何明一，卫保国.数字图像处理[M].北京：科学出版社，2008.

[3]韩力群.人工神经网络理论、设计及应用[M].北京：化学工业出版社，2007.

[4]周日贵，姜楠，丁秋林.量子Hopfield神经网络及图像识别[J].中国图象图形学报，2008，13（1）：119-123.

ZHOU Ri-gui，JIANG Nan，DING Qiu-lin.Quantum Hopfield neural network and image recognition[J].Journal of Image and Graphics，2008，13（1）：119-123.

[5]兰雪梅，朱建，黄承明，等.BP网络的MATLAB实现[J].微型电脑应用，2003，19（1）：6-8.

LAN Xue-mei，ZHU Jian，HUANG Cheng-ming，et al.BP network realization in MATLAB[J].Microcomputer Application，2003，19（1）：6-8.

[6]张海波，董槐林，龙飞，等.基于BP神经网络的图像识别研究[J].计算机与现代化，2008（5）：17-19.

ZHANG Hai-bo，DONG Huai-lin，LONG Fei，et al.Research on image recognition based on BP neural network[J].Computer and Modernization，2008（5）：17-19.

[7]张浩然，韩正之，李昌刚.基于MATLAB的神经网络辨识与控制工具箱[J].计算机仿真，20（3）：72-74.

ZHANG Hao-ran， HAN Zheng-zhi， LI Chang-gang.Neural network based system identification and control toolboxes in MATLAB environment[J].Computer Simulation，20（3）：72-74.

[8]戚德虎，康继昌.BP神经网络的设计[J].计算机工程与设计，1998，19（2）：48-50.

QI De-hu，KANG Ji-chuang.Design of the BP neural network[J].Computer Engineering and Design，1998，19（2）：48-50.