我国股市风格资产收益的双长记忆性研究

喻国平，许 林

(1.江西财经大学 经济学院，南昌 330013；2.华南理工大学 经济与贸易学院，广州 510006)

0 引言

近年来，金融时间序列是否存在长记忆性研究是现代金融理论的热点问题，国内学者对股市收益序列的长记忆性研究较多，但所得出的结论却不尽相同。大部分学者认为我国沪深股市日收益率序列均存在显著的长记忆性特征，但也有一小部分学者认为我国沪深股市日收益率序列的长记忆性均不显著或至少有一个长记忆性不显著；另外，还有学者认为我国深市日收益率序列的长记忆性特征不显著，而股市波动过程却存在显著的长记忆性特征。不同学者的研究结论之所以出现差异，主要是因为所采用的方法和选择的样本不同。目前，检验时间序列长记忆性的方法主要有两类：统计方法和数学模型方法。统计方法主要包括R/S分析、DFA和小波分析等方法，数学模型方法主要包括均值方程的AR(FI)MA模型和方差方程的长记忆GARCH族模型。传统的统计方法必须通过对日收益序列的收益率和波动率分别进行分析才能得到双长记忆性存在与否的结论，而数学模型方法却可直接通过对收益和波动序列进行建模，利用极大似然估计等方法同时估算出所有的长记忆性参数，这既避免了逐个考察的数据普适性问题，又有助于兼顾收益率与波动率之间的相互影响。通过梳理国内外相关文献不难发现：已有分形计量模型应用研究文献基本都集中在股票综合指数方面，在基金投资领域中鲜有学者涉及，Sharpe最早研究发现投资风格对基金业绩的贡献度达90%以上；国内学者曹雪平(2011)对我国证券投资基金的业绩表现进行实证研究，结果也认为投资风格可有效解释基金的业绩表现，并认为市场态势是影响基金投资风格的重要因素[1]。投资风格研究已越来越受到学者们的青睐，风格投资也就成了基金经理构建投资组合的主流投资方法。投资风格是基金产品发行、设计考虑的主要因素；而风格投资是基金投资运作中采取的具体风格轮换或漂移策略。把两者联系起来创新性地为基金经理提出了一种适度风格漂移量化投资策略，将其定义为投资风格的风格投资策略。那么要想成功构建这种漂移策略，就必须分析我国股市风格资产是否具有分形特征，挖掘出适度风格漂移的时点。带着这些问题的探索，本文引入偏t分布下的ARFIMA-HYGARCH计量模型来实证我国股市风格资产收益序列的双长记忆性分形特征，以期为基金经理与投资者挖掘到有价值的波动信息。

1 skt-ARFIMA(p1,d1,q1)-HYGARCH(p2,d2,q2)模型构建

双长记忆性模型是GARCH族模型的衍生形式，采用长记忆的时间序列模型来分别刻画条件均值方程和条件方差方程，然后通过拟极大似然法估计其参数，本文采用ARFIMA模型估计条件均值方程，HYGARCH模型估计条件方差方程，并引入刻画尖峰厚尾特征的skt分布来进行分布拟合，下面对skt-ARFIMA(p1,d1,q1)-HYGARCH(p2,d2,q2)模型进行介绍。

Andersen,Bollerslev,Diebold&Ebens(2001)提出用自回归分整移动平均(ARFIMA)模型可较好刻画时间序列的长记忆过程，ARFIMA(p,d,q)模型是整数阶差分ARIMA模型的推广形式，允许对序列进行分数d阶差分，综合考虑了长记忆过程和短记忆过程，是用p+q个参数来描述短记忆过程，用参数d描述长记忆过程，可以较好模拟那些相关程度比ARMA过程强，但又比ARIMA过程弱的时间序列，因此既优于单纯描述短记忆过程的ARMA(p,q)模型，又优于单纯描述长记忆过程的FDN模型。由于我国证券市场还很不成熟，呈复杂的分形特征，因此本文采用ARFIMA模型对股市风格资产日收益序列进行模拟是合适的。

Davidson(2004)通过在FIGARCH模型的滞后项中引入新参数â进行扩展，提出了HYGARCH模型，通过参数d来度量序列波动过程的双曲线记忆，求解得到的是lnα，当α=1即lnα=0时就变成了FIGARCH模型。ARFIMA(p1,d1,q1)-HYGARCH(p2,d2,q2)模型具体形式为：

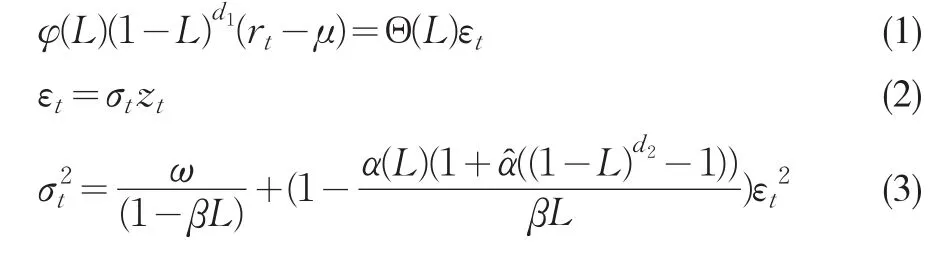
其中，L为滞后算子，|d1|＜0.5，μ为平稳时间序列{Rt}的无条件均值，zt为新生变量，服从均值为0，方差为1的独立同分布，(1)式为ARFIMA(p1,d1,q1)模型的条件均值方程，(2)式新生变量分布或残差分布，(3)式为HYGARCH(p2,d2,q2)模型的条件方差方程。

序列收益过程的长记忆性是由(1)式中的参数d1刻画，当0＜d1＜0.5时，序列{ }Rt为长记忆性平稳过程，即持久性；当-0.5＜d1＜0时，序列{ }Rt为短记忆性平稳过程，即反持久性。另外，当d1=1时，ARFIMA(p1,1,q1)模型退化为ARIMA模型；当d1=0时，ARFIMA(p1,0,q1)模型退化为ARMA(p1,q1)模型；当p1=q1=0且μ=0时，ARFIMA(0,d1,0)模型就退化为FDN模型。

序列波动过程的长记忆性是由(3)式中的参数d2刻画，当d2＞0时，序列{Rt}的波动率具有长记忆性，即持久性。此时，)模型的振幅为(1-â)。作为HYGARCH(p2,d2,q2)模型的特殊情况，平稳FIGARCH模型和GARCH模型分别对应于â=1和â=0的情形。因此，HYGARCH模型可克服FIGARCH模型的一些限制，具有以下特点：(1)HYGARCH模型是协方差平稳的(â≠1)；(2)HYGARCH模型可对记忆参数d2和振幅参数S分别进行估计，避免了FIGARCH模型中S=1的约束；(3)当 0＜d2＜1时，序列记忆长度随着d2的增加而增加。

这里假定新生变量zt服从skt分布，其概率密度函数为：

其中，g(·|d)为标准对称t分布的概率密度函数，s是偏度系数，d是自由度，d越小，表示尖峰厚尾特征越明显，分别是skt分布的均值与标准差。

2 实证研究

2.1 样本选取与数据处理

本文采用中信标普公司推出的6种纯风格资产指数(即大盘纯成长指数(LPG)、大盘纯价值指数(LPV)、中盘纯成长指数(MPG)、中盘纯价值指数(MPV)、小盘纯成长指数(SPG)和小盘纯价值指数(SPV))日收盘价格，数据期间为2005年7月1日至2010年3月26日，包含大幅上涨、快速下跌和小幅回调等一个完整的周期行情，具有较好的代表性。样本容量为1031个日收盘价，为了减弱数据的非平稳性，样本数据采用对数收益率，设pt表示t日风格资产的收盘价，则t日的风格资产收益率为：rt=lnpt-lnpt-1，可计算出1030个日收益率序列。数据来源于中信标普公司网站(www.spcitic.com)，数据处理与实证分析采用OXmetrics5.1与Eviews6.0软件，采用拟极大似然估计方法对参数进行估计。

本文选用中信标普风格指数系列的原因是基于以下3点考虑：一是很多基金产品在设计投资风格时是以中信标普风格指数为参考标准的；二是至今为止中信标普风格指数是能够较好反映我国股市纯风格指数之一；三是大量实证研究也表明：该风格指数的编制方法是合理的，能较好反映我国证券市场不同风格资产的风险收益特征。该纯风格指数系列编制的原则为：三分之一的成份股为纯成长股，三分之一的成份股为纯价值股，中间三分之一的成份股不作为纯风格指数，因此不会出现交叉重叠的股票，且样本股票是根据风格属性进行赋权，能较好地反映各种风格属性特征。

2.2 样本数据基本统计特征

为了对我国股市风格资产日收益序列有个基本的判断，表1给出了这6种风格资产日收益序列的描述性统计量及单位根、独立同分布检验结果。

从表1中可以看出：该6种风格资产指数日收益率序列的偏度均不为0，表明风格资产收益序列是不对称分布，表现出一定的左偏或右偏特征；峰度均大于3，表明具有尖峰特征；JB统计量在1%显著性水平下均拒绝正态分布的原假设，表明均不服从正态分布；ADF统计量在1%显著性水平下均拒绝存在单位根的原假设，表明为平稳序列；运用BDS检验的Z统计量进行独立同分布检验，结果均拒绝了独立同分布的假定。因此，采用ARFIMA模型对风格资产日收益序列进行建模是合适的。

2.3 模型确定与参数估计

本文在确定ARFIMA-HYGARCH模型的具体阶数时，不是采用通常的GARCH(1,1)模型来刻画条件方差的时变性，而是用数据说话，利用4个信息准则值的最小化原则来选择最优ARFIMA-HYGARCH模型的具体阶数，为了充分刻画数据的尖峰厚尾特征，假定残差序列服从skt分布。限于文章的篇幅，仅列出大盘纯成长风格资产ARFIMA-HYGARCH模型阶数的确定过程(见表2)。

表1 风格资产日收益率序列的基本统计特征

表2 大盘纯成长风格资产日收益序列的ARFIMA-HYGARCH模型阶数的确定

通过表2中的计算结果表明：选择skt-ARFIMA(1,d1,1)-HYGARCH(1,d2,0)模型是最合适的，因为该模型的4个信息准则有3个信息准则值达到最小。同理对其它5种风格资产日收益序列进行模型阶数的确定，得出相同的结论，具体计算结果略，有需要者可向作者索取。下面就采用skt-ARFIMA(1,d1,1)-HYGARCH(1,d2,0)模型对6种股市风格资产日收益序列进行参数估计，结果见表3所示。

表3 6种股市风格资产日收益序列在skt分布下的ARFIMA(1,d1,1)-HYGARCH(1,d2,0)模型参数估计结果

从表3中的模型参数估计结果发现：刻画序列收益过程的长记忆性参数d1，6种风格资产在0.05的显著性水平下均满足0＜d1＜0.5，说明序列{Rt}为长记忆性平稳过程，即持久性；刻画序列波动过程的长记忆性参数d2，6种风格资产在0.05的显著性水平下均满足d2＞0，说明序列{Rt}的波动过程具有长记忆性，且还满足0＜d2＜1，进一步表明这6种风格资产日收益序列记忆长度随着d2的增大而增加。lnξ不等于0，表明收益序列有偏，ν显著较大，表明收益序列具有明显的尖峰厚尾特征，这些与表1的描述性统计结果相一致。

2.4 skt分布的Person吻合度检验

Palm和Vlaar研究发现Pearsonχ2吻合度检验能够比较真实分布和理论分布的接近程度，检验步骤是将标准化残差序列{êt}按大小分成g个单元，ni是第i个单元的观测数，在理论分布是真实分布的原假设下，构建统计量的渐进分布界于χ2(g-1)与χ2(g-k-1)之间，k是参数个数，并指出对样本容量N=2252，可设g=50。对于本文选择的研究样本容量N=1030，我们大约取g=30。Person吻合度检验结果见表4。从表4中的修正Person吻合度检验结果知道：在0.01显著性水平下均不能拒绝服从skt分布的原假设，即由ARFIMA(1,d1,1)-HYGARCH(1,d2,0)模型所生成的新生变量，假定其服从skt分布是合理的。

3 结论

本文以中信标普公司推出的6种股市纯风格资产指数为样本，运用ARFIMA-HYGARCH最新计量模型研究了我国股市风格资产日收益序列的收益与波动过程的双长记忆性特征，通过4个信息准则确定skt-ARFIMA(1,d1,1)-HYGARCH(1,d2,0)为最优模型，在模型的参数估计结果中，在0.05的显著性水平下，刻画长记忆性的参数d1,d2均显著在(0,1)区间内，表明我国股市风格资产序列的收益与波动过程均具有较强的长记忆性特征。Person吻合度检验证实了在0.01的显著性水平下，skt分布是股市风格资产日收益序列的真实分布。该研究结论与方法为基金公司、基金经理捕捉股市风格轮换时机、构建适度风格漂移策略以获取短期超额收益提供了理论支持与决策参考。

本文所构建的双长记忆性计量模型只是基于单一分形分析的长记忆特征分析模型，不能同时刻画股市风格资产收益或波动过程的多重分形特征。因此，如何运用多重分形分析方法对我国股市风格资产收益序列的多重分形特征进行分析以及构建出双长记忆性多重分形计量模型将是下一步重点研究的方向。

表4 修正的Personχ2吻合度检验

[1] 曹雪平.不同态势下基金风格和绩效[J].系统工程,2011,29(5).

[2] 赵桂芹,曾振宇.证券市场长期记忆特征的实证分析[J].管理科学,2003,16(2).

[3] 曹广喜,史安娜.基于R/S分析的上海证券市场的指数和交易量的分形特征分析[J].华东经济管理,2006,20(7).

[4] 许林,宋光辉,郭文伟.基于R/S分析的股市风格分形特征研究[J].商业研究,2011,(1).

[5] 张卫国,胡彦梅,陈建忠.中国股市收益及波动的ARFIMA-FI⁃GARCH模型研究[J].南方经济,2006,(3).

[6] 李海奇,屠新曙,段琳琳.中国股票市场波动长记忆建模研究[J].统计与决策,2006,(8).

[7] Bollerslev.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econo Metrics,1986,31(3).

[8] Nelson.Conditional Heteroskedasticity in Asset Returns:A New Ap⁃proach[J].Econometrica,1991,59(2).

[9] Fernandez C.,Steel M.F.J.On Bayesian Modeling of Fat Tails and Skewness[J].Journal of the American Statistical Association,1998,93(441).

[10] Davidson,J.Moment and Memory Properties of Linear Conditional Heteroscedasticity Models,and a New Model[J].Journal of Business and Economic Statistics,2004,22(1).

[11] Andersen T.G,Bollerslev T,Diebold F.X,Ebens H.The Distribution of Realized Stock Return Volatility[J].Journal of Financial Economics,2001,61(1).

[12] Wilson Kwana,Wai Keung Lib,Guodong Lib.On the Estimation and Diagnostic Checking of the ARFIMA-HYGARCH Model[J].Compu⁃tational Statistics&Data Analysis,2010,(7).