基于相关系数及IOWA算子的区间组合预测方法

陈华友，李 翔，金 磊，姚梦杰

(安徽大学数学科学学院，合肥230601)

0 引言

传统的预测方法都是使用单项预测方法对目标进行预测，但是这种预测是存在风险的，一旦单项预测方法选择错误，就会使得最后的预测误差较大，给我们的决策带来麻烦。为了分散这种风险，Bates和Granger[1]首次提出组合预测方法的概念并进行了相关的研究。此外，现实生活中，由于客观事物的复杂性、不确定性以及人类思维的模糊性，在实际决策问题中，决策信息往往以区间数形式[2]来表达。为了综合信息的这种不确定性，文献[3]引进区间组合预测。

传统的组合预测方法[4]-[5]大都局限在对于不同的单项预测方法赋予相应的固定加权系数，这便忽略了各单项预测方法在不同时点预测精度的不同，因此固定加权的组合预测方法也存在一定的缺陷。美国著名学者Yager提出了有序加权平均算子[6]和诱导有序加权平均算子[7](Induced Ordered Weighted Averaging Operator)的概念，文献[8]建立了基于IOWA算子的组合预测模型，它根据不同时点预测精度的作为诱导变量给各单项预测值进行有序加权平均，这实际上是一种变权组合预测方法。

同时，我们注意到传统的组合预测方法大都是以不断改善拟合误差平方和为基础来建立模型，从而求出权系数，然而文献[9]给出了研究组合预测的另一新途径，即提出了基于相关性指标的最优组合预测模型的研究。本文在此基础上，结合IOWA算子，针对预测值与实际值都以区间数形式给出的问题，从相关系数角度出发，对区间中点和区间半径进行研究，建立基于相关系数及IOWA算子的区间组合预测模型，并探讨了权系数求解方法。从最后的实例分析结果可以看出，本文的模型可以提高预测的精度。

1 预备知识

定义1称a={x|aL≤x≤aU,aL,aU∈R}为区间数，令ma=1 2(aL+aU)，ra=1 2(aU-aL)，则称ma为a的区间中点，称ra为a的区间半径。此时区间数a也可记为a=[aL,aU]或用区间中点和区间半径的表达形式a=(ma,ra)。

设区间数a=[aL,aU]=(ma,ra)，b=[bL,bU]=(mb,rb)，则a，b之间有如下二元运算关系：

（1）加法运算：

a+b=[aL+bL,aU+bU]=(ma+mb,ra+rb)

（2）减法运算：

a-b=[aL-bU,aU-bL]=(ma-mb,ra+rb)

（3）数乘运算：λa=[λaL,λaU]=(λma,λra)，其中λ≥0 。

定义2[8]设fw:Ωn→Ω 为n元函数,若fw(α1,α2,…,，其中是与fw有关的加权向量,满足是(α1,α2,…αn)中按降序排列的第i个大的数，则称函数fw是n维有序加权平均算子，简记为OWA算子，Ω表示实数集。

定义2表明OWA算子对序列(α1,α2,…αn)排序过后的加权平均，其中( )w1,w2,…,wn只与序列按降序排列后的位置i有关，而与序列(α1,α2,…αn)无关。

定义3[6]设为n个二维数组，令，其中有关的加权向量，满足ex(i)是u1,u2,…,un中按降序排列的第i个数的下标，则称函数IOWAw是由u1,u2,…,un所产生的n维诱导有序加权算术平均算子，简称为IOWA算子，ui称为ai的诱导值。

定义3表明IOWA算子是借助诱导序列(u1,u2,…,un)，先对诱导序列进行降序排列，再根据诱导序列排列后的第i大元素的对应原始序列中的元素αu-index(i)，对其赋予权系数wi进行有序加权平均。显然，IOWA算子的权系数只与诱导值所在的位置有关，而与序列(α1,α2,…αn)无关。

2 基于相关系数及IOWA算子的区间组合预测模型

定义4令:

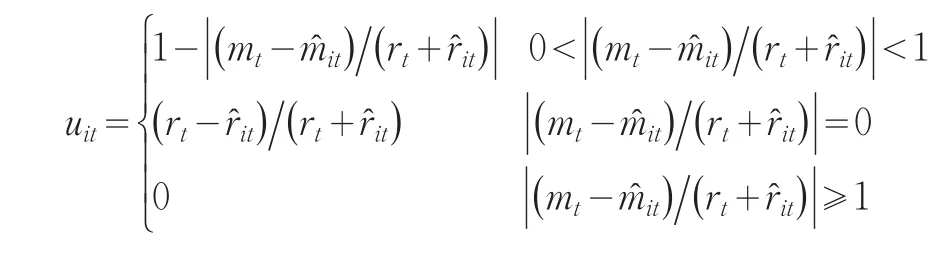
则称uit为第i种预测方法在第t时刻的预测精度，其中uit∈[0,1] ，i=1,2,…,p;t=1,2,…,N。

定义4可以得到时刻t下的一组预测精度的序列u1t,u2t,…,upt，将此序列与预测序列1t,2t,…,pt结合便可得到p个二维区间数组由定义2.3将序列u1t,u2t,…,upt作为诱导值序列，对区间预测序列1t,2t,…,pt进行如下的运算。

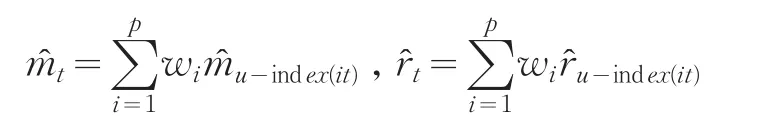
显然，IOWA算子区间组合预测是根据不同时刻各种预测方法预测精度的不同而赋予不同的权系数。由于区间中点和区间半径是反映区间数本质特征的两个重要指标，两个区间数相等当且仅当他们的中点和半径分别相等。因此，两个区间数序列的相关程度可以用区间数的中点和半径序列的相关系数来度量，为此引入下面的定义：

定义6令：

则称Rm为IOWA算子的区间组合预测值t中点序列{t,t=1,2,…,N}与实际区间观察值中点序列{mt,t=1,2,…,N}的相关系数，称Rr为它们相应的半径序列{,t=1,2,…,N}与实际区间观察值中点序列{rt,t=1,2,…,N}的 相 关 系 数 ，其 中

显然Rm,Rr∈[0,1]，Rm和Rr越接近于1，则表明IOWA算子的区间组合预测值序列与实际区间观测值序列之间的预测误差就越小。

结合定义6以及上面的记号和运算式，可将区间中点序列相关系数Rm和半径序列相关系数简化为：显然区间组合预测值与实际区间观测值的中点序列和半径序列的相关系数均是权向量W=(w1,w2,…,wp)T的函数，可分别记为Rm(W)和Rr(W)，为了使得区间组合预测结果与实际区间值更为接近，则应最大化相应的相关系数指标，即建立如下基于相关系数及IOWA算子的区间组合预测模型：

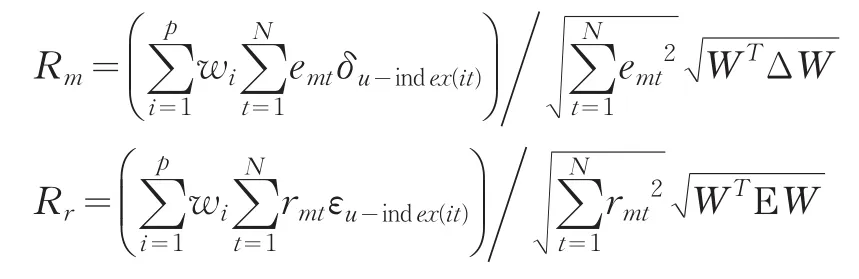
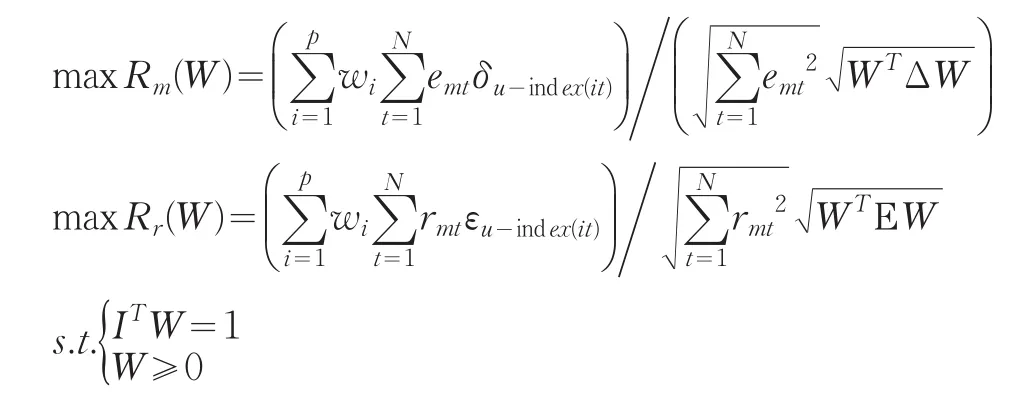
其中I=(1 ,1,…,1)T为元素全为1的n维向量。

上述区间组合预测模型为多目标非线性规划问题。为了求解该模型，本文引入参数ρ，将多目标非线性规划问题转化为单目标非线性规划问题，得到如下最优化模型：

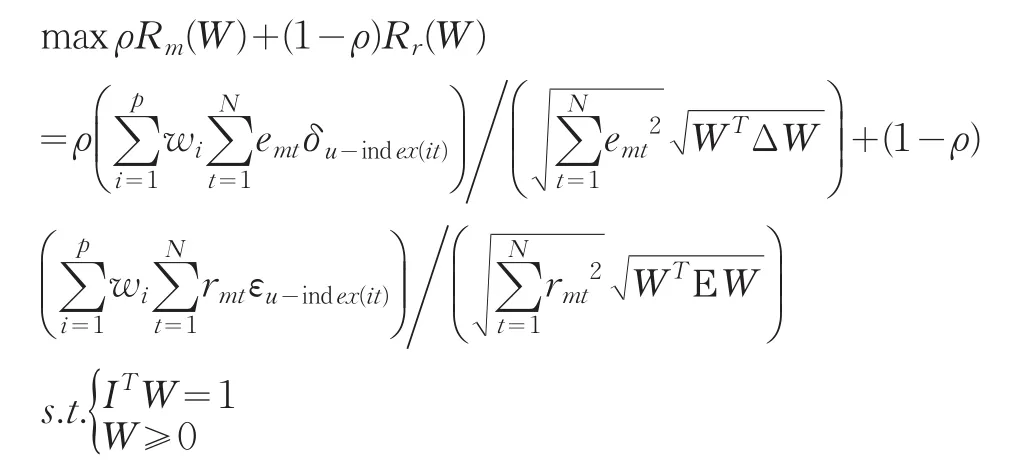
其中I=(1 ,1,…,1)T，参数ρ是对区间中点相关系数的重要性程度的度量。此模型为非线性规划问题可以使用MATLAB优化工具箱进行求解。

3 实例分析

为了说明基于相关系数及IOWA算子的区间组合预测模型的有效性，利用文献[9]的数据，对本文提出的模型进行实例分析。表1给出了实际区间与各单项预测方法区间预测资料。

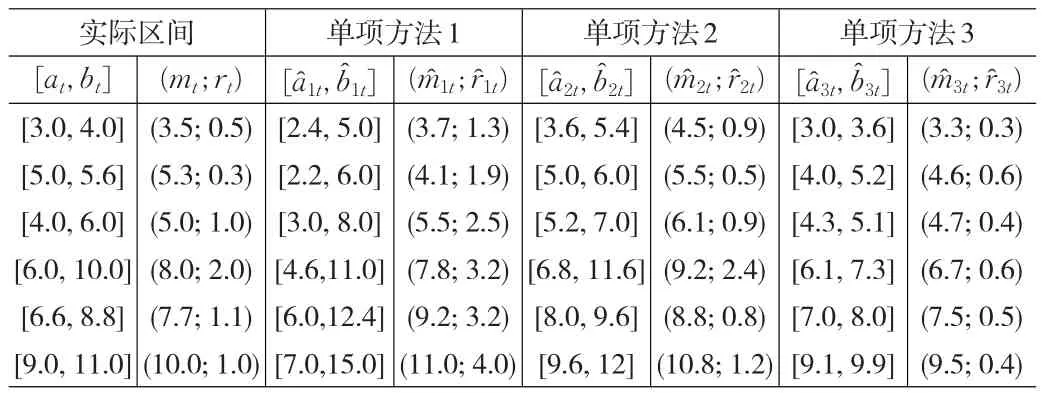
表1 实际区间值和各单项预测方法区间预测值

根据定义4，可以计算各单项预测方法各时点预测精度，结果见表2：

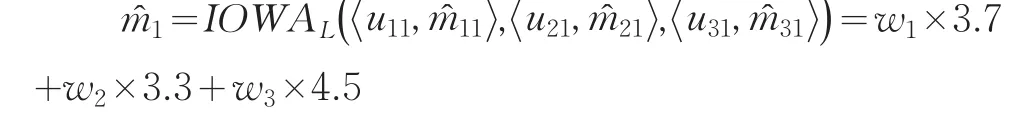
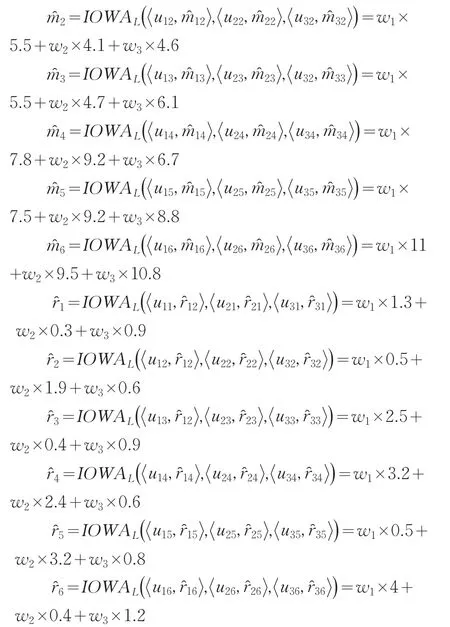
将上述表达式代入到单目标非线性规划的区间最优化组合预测模型中，取ρ=0.5，再利用MATLAB软件计算，可得基于相关系数及IOWA算子的区间组合预测模型的最优权系数为:

w1=0.5042w2=0.4958w3=0.0000

为检验区间组合预测效果，本文引入4种误差指标进行模型效果分析，4种误差指标如下：

（1）平均区间中心位置误差平方和

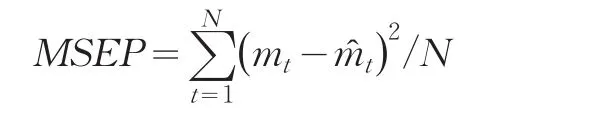
（2）平均区间长度误差平方和

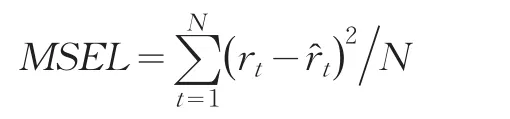
（3）平均区间误差平方和MSEI=MSEP+MSEL

（4）平均区间相对误差和

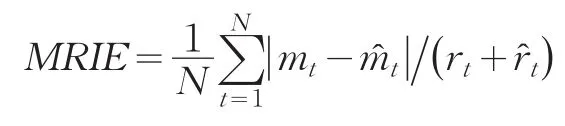
具体计算结果如表3所示。

从表3可以看出基于相关系数及IOWA算子的区间组合预测模型的四项误差指标均显著小于各单项预测方法误差指标，只有MSEL不够显著，但也并非最大，这表示此方法至少是非劣性的，综合来看，基于相关系数及IOWA算子的区间组合预测模型是能够很好的提高预测精度的。下面讨论ρ选取对最优化模型的权重系数的影响。表4给出ρ的灵敏度分析结果。

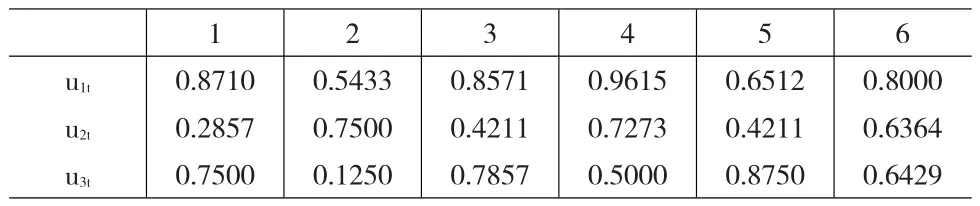
表2 各单项预测方法各时点预测精度

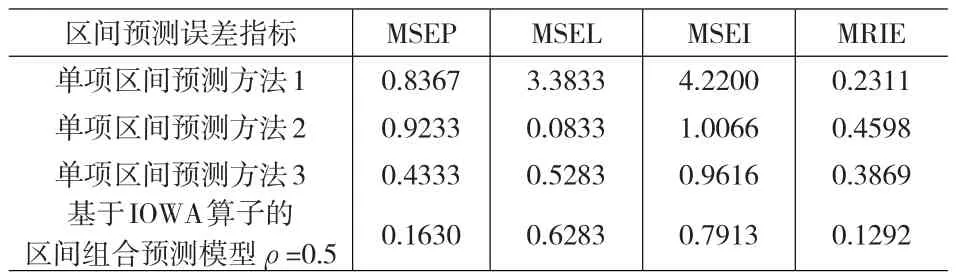
表3 各项区间组合预测误差指标

表4 对ρ的灵敏度分析

从表4中可以看出随着ρ的增加，权系数w1和w2的值主要集中在0.5附近，权系数w3全为0。这表明，预测最差的预测值是冗余的，它不参与组合预测。同时随着ρ的增加，目标函数值在不断增大且趋近于1。

类似地，下面的图1给出ρ选取的不同值对四个误差指标MSEP,MSEL,MSEI,MRIE的影响情况。

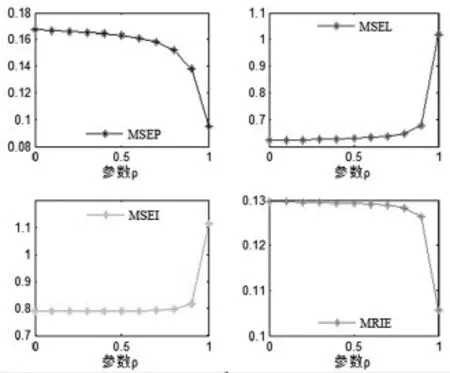
图1 参数ρ选取的对不同误差指标的灵敏度分析

显然从图1中可以看到MSEP以及MRIE随着ρ的增加而减小，MSEL以及MSEI随着ρ的增加而增大，当ρ接近于1时四项指标的变化较为剧烈，当ρ≤0.8时四项指标的变化都是较为平缓的，因此我们可以选取ρ≤0.8，这样都会得到不错的预测效果。

4 结束语

本文建立了基于相关系数及IOWA算子的区间组合预测模型，并且从实例上验证了模型的有效性，但是有关区间组合预测有效性理论的研究仍有待于进一步探讨。即对于区间组合预测模型，如何定义的优性，非劣性区间组合预测方法及其相关冗余预测方法的判定等问题，仍需研究。

[1] Bates J.M.Granger C.W.J.Combination of Forecasts[J].Operations Research Quarterly,1969,20(4).

[2] Yoon K.The Propagation of Errors in Multiple-attribute Decision Analysis:A Practical Approach[J].Journal of the Operational Re⁃search Society,1989，（40）.

[3] 沈家骅,严振祥.基于区间分析的组合预测系数确定方法[J].武汉理工大学学报,2006,30(6).

[4] 唐小我，马永开，曾勇，杨桂圆.现代组合预测和组合投资决策方法及其应用[M].北京：科学出版社，2003.

[5] 陈华友，侯定丕.基于标准差的预测有效度的组合预测模型[J].系统工程学报，2003,18(3).

[6] Yager R.R.,On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decision Making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988，（18）.

[7] Yager R R.Induced Aggregation Operators[J].Fuzzy Sets and Systems,2003，（137）.

[8] 陈华友.基于预测有效度的组合预测模型研究[J].预测，2001，20(3).

[9] 王应明.基于相关性的组合预测方法研究[J].预测，2002，21(2).

[10] 徐惠莉，吴柏林，江韶珊.区间时间序列预测准确度探讨[J].数量经济技术经济研究，2008，25(1).