螺旋桨四象限水动力性能数值模拟及应用
李 理,刘 可,李 超,肖 冰,石爱国
(海军大连舰艇学院,辽宁 大连 116018)
螺旋桨四象限水动力性能数值模拟及应用
李 理,刘 可,李 超,肖 冰,石爱国
(海军大连舰艇学院,辽宁 大连 116018)
在螺旋桨数值模拟领域里,敞水桨四象限(前进中正车、前进中倒车、后退中进车、后退中倒车)的水动力性能研究几乎是空白。本文从桨的几何构建,网格生成,第一、四象限和第二、三象限的不同求解模式及流场特征,第二、三象限推力系数曲线拐点及相应的环流涡,进行了数值模拟和分析。对桨四象限的应用,以制动机动为例进行探讨。
螺旋桨;水动力性能;四象限;数值模拟
0 引言
以螺旋桨的数值模拟部分取代桨模的试验,是当前螺旋桨CFD研究的一个热点,但其中敞水桨四象限水动力性能的数值模拟几乎是空白。这一领域的研究不仅具有理论意义,而且是解决舰船操纵性和速航性诸多实际课题(离靠泊、舰船避碰、各种特殊机动)的关键所在。
桨的四象限水动力模拟,不是桨的第一象限(正车前进)敞水性能模拟的简单推广。桨的第一、四象限的流场,具有弱非线性特征,它的CFD求解模式相对简单;而桨的第二、三象限的流场具有较强的非线性,需要采用不同于第一、四象限的求解模式,才能得到较精确的解。本文在求解第二、三象限敞水性能曲线过程中,伴随着拐点的出现,发现流场会生成明显的环流涡,从而使第二、三象限的非线性性质在力学和数学上都得到有力的验证。
1 螺旋桨的几何建模
以AU系列螺旋桨中的AU5-65型螺旋桨为研究对象。1959年奥本明良[1]对该型桨进行了四象限敞水系列试验,依据奥本的试验,确定桨的几何尺度如下:叶数 Z=5,螺距比P/D=1.00,盘面比AE/AO=0.65,桨直径D=0.25 m,纵斜角10°。
桨体几何建模时,需利用螺旋桨的基本要素、桨叶轮廓尺寸表以及叶切面尺寸表等二维型值数据,建立螺旋桨的三维型值。桨叶剖面参数如图1所示。

图1 桨叶剖面Fig.1 Blade section
通过螺旋桨的基本参数和各桨叶切面二维形状尺寸,可建立螺旋桨空间三维坐标关系式:

式中:xr为桨叶剖面的纵斜;θs为桨叶剖面的侧斜;β为桨叶的螺距角;db,f为桨叶叶面、叶背到弦线的距离;s为剖面上任意点至导边的弦线距离;c1为弦线中点至导边的距离。
在计算得到的各剖面三维坐标型值点的基础上,借助Pro/E软件,经一系列步骤,可生成AU5-65桨的三维几何模型,如图2所示。

图2 AU5-65螺旋桨三维实体模型Fig.2 AU5 -65 Propeller 3D solid model
2 AU5-65型螺旋桨水动力的数值模拟
2.1 计算域建立与网格划分
2.1.1 计算域的建立
对于第一、四象限工况,流场相对平顺,计算域可相对小一些;对于流场较为复杂的二、三象限工况,计算域要相对加大,以减小边界处对螺旋桨复杂流场的影响。本文设置情况如表1所示。

表1 计算域设置Tab.1 Computational domain setting
2.1.2 网格形式
Fluent可提供的处理旋转流场的方法有多重参考系(MRF)、混合面法及滑移网格3种。针对螺旋桨水动力计算的数值模拟,一般多采用MRF与滑移网格2种方法。
对AU型螺旋桨,采用滑移网格方法进行了4个象限的敞水性能数值模拟。网格形式采用分区混合网格,靠近螺旋桨的小旋转域由于桨叶扭曲较大,采用非结构性四面体及棱柱形边界层网格,计算域其余部分采用结构性六面体网格。为保持小旋转域与计算域其余部分的交界面处的网格的一致性,减少截断误差,采用一层金字塔形五面体网格进行过渡,如图3所示。

图3 交界面处的金字塔形网格Fig.3 At the interface of Pyramid grid
2.1.3 网格划分
1)桨叶表面网格划分
采用尺度函数(size function)方法,对桨叶导边、随边、叶梢、叶根等流场变化复杂的部位布设尺度为0.002 5D的三角形面网格,以增长率Growth Rate=1.1向叶片中心等流场变化相对平缓的区域扩张,最大网格尺度限制在0.016D。划分好的桨叶面网格如图4所示。

图4 AU型桨桨叶面网格分布Fig.4 AU type propeller blade grid distribution
2)桨叶近壁区的处理
虽然螺旋桨的旋转流场相对复杂,湍流现象十分明显,但在贴近桨叶表面区域,仍然存在粘性底层。在这一区域内,几乎完全是层流,因此对非线性强的第二、三象限需在这一区域采用相对细密的网格,并在计算上作特殊处理。取y+≈40,确定第一层网格厚度为ΔyP=0.000 25 m。由于桨叶表面采用的是三角形非结构性网格,因此紧贴桨叶表面的边界层区域可采用棱柱形五面体网格填充。网格生成可使用前处理软件TGrid完成:以第一层为基础,按增长率1.1共生成5层边界层,如图5所示。

图5 桨叶表面边界层网格分布Fig.5 The blade surface boundary layer mesh distribution map
3)总网格情况
第一、四象限:共生成108万个网格,包含螺旋桨的小圆柱体旋转计算域部分生成四面体非结构性网格88万个,大计算域部分生成六面体结构性网格20万个。
第二、三象限:采用大计算域,入流口至桨盘面的距离与出流口至桨盘面的距离相等,均为6倍的螺旋桨直径D,共生成182万个网格。其中五片桨叶的边界层区域共生成棱柱层网格45万个,小旋转计算域其余部分生成四面体非结构性网格93万个,大计算域部分生成六面体结构性网格44万个。
具体网格情况如图6所示。

图6 AU型桨计算域设置及网格划分Fig.6 Computational domain setting and grid of AU type propeller
2.2 边界条件
对AU型桨四象限数值模拟试验采用滑移网格方法,边界条件设置情况如下:上游入流口边界面设置为速度入口;下游出流口边界面设置为压力出口,并给定出口边界静压值为0。计算域圆柱体表面设置为无滑移固定壁面;螺旋桨桨叶与桨毂设置为无滑移旋转壁面,与邻域保持相对旋转速度为0;小旋转域与计算域其余部分的交界设为Interface,并控制小旋转域围绕X轴以预定的角速度旋转。第一象限给出边界条件的设置如图7所示。对于第二、三、四象限的边界条件,只需根据螺旋桨旋转方向与来流方向的不同进行相应改动即可。
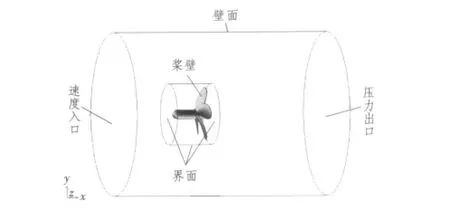
图7 边界条件设置Fig.7 Setting of boundary condition
2.3 敞水性能的数值模拟结果及分析
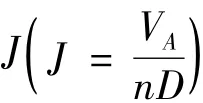
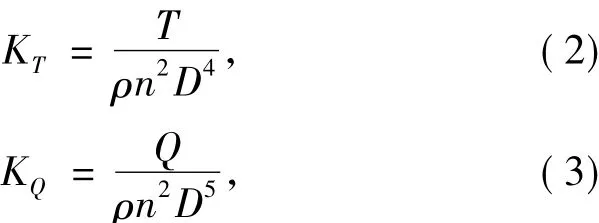

式中:D为螺旋桨直径;ρ为水的密度;T为螺旋桨推力;Q为螺旋桨转矩。
文献[1]在进行AU桨的四象限桨模水池试验时,桨模保持转速N=660 r/min不变,雷诺数Re=7.19×105。本文也设螺旋桨转速N=660 r/min,通过逐步增大入口流速的方式来改变进速系数J。湍流选取RNG k-ε湍流模型。
2.3.1 第一象限
进速系数J=0.1~0.4范围的计算结果如表2所示,敞水性能曲线如图8所示。
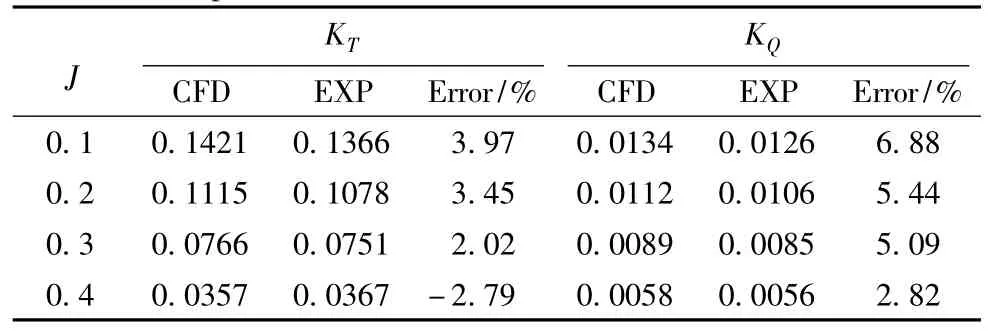
表2 AU型桨第一象限敞水性能数值模拟结果Tab.2 The first quadrant AU type propeller open water performance numerical simulation
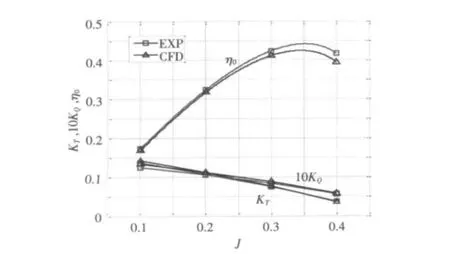
图8 AU型桨第一象限敞水性能数值模拟曲线Fig.8 Open water performance of the first quadrant numerical simulation curve of AU type propeller
2.3.2 第二象限对于第二象限与第三象限,本文只进行了水池试验值较准确[1]的进速系数J≤-0.4范围内的试验,结果如表3~表4及图9~图10所示。
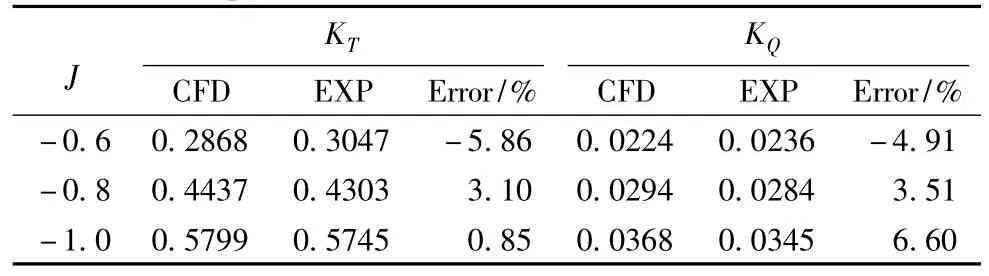
表3 AU型桨第二象限敞水性能数值模拟结果Tab.3 Type AU paddle second quadrants open water performance numerical simulation

图9 AU型桨第二象限敞水性能数值模拟曲线Fig.9 AU type propeller second quadrant open water performance numerical simulation curve
2.3.3 第三象限

表4 AU型桨第三象限敞水性能数值模拟结果Tab.4 AU type paddle third quadrants open water performance numerical simulation
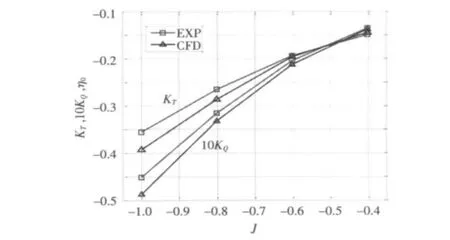
图10 AU型桨第三象限敞水性能数值模拟曲线Fig.10 Numerical simulation of third quadrant open water characteristics curve
2.3.4 第四象限
计算结果如表5和图8所示。
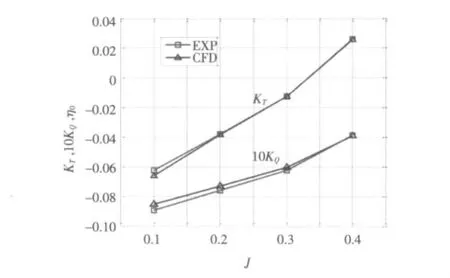
图11 AU型桨第四象限敞水性能数值模拟曲线Fig.11 Numerical simulation of fourth quadrant open water characteristics curve
由表2、表5及图8、图11可以看出,第一象限、第四象限数值计算值与水池试验值吻合良好,KT与KQ的最大误差不超过8%。随着螺旋桨进速系数减小,螺旋桨载荷增加,KT与KQ的误差有增大的趋势;对于螺旋桨效率η0来说,普遍偏小,原因是采用了相对粗大的桨毂而降低了效率。对于第二、三象限,误差在合理范围内。
2.4 螺旋桨周围流场
数值模拟的一大优势是能精细地描述和再现流场的细节,为研究桨的水动力规律提供依据。
2.4.1 桨叶压力分布
以第四象限为例,其桨叶压力面、吸力面等值线分布情况如图12所示。

图12 第四象限桨叶表面压力分布Fig.12 Fourth quadrant of the blade surface pressure distribution
2.4.2 桨叶周围的压力场
图13为桨叶半径比为r/R=0.4处的桨叶前后压力场分布图。
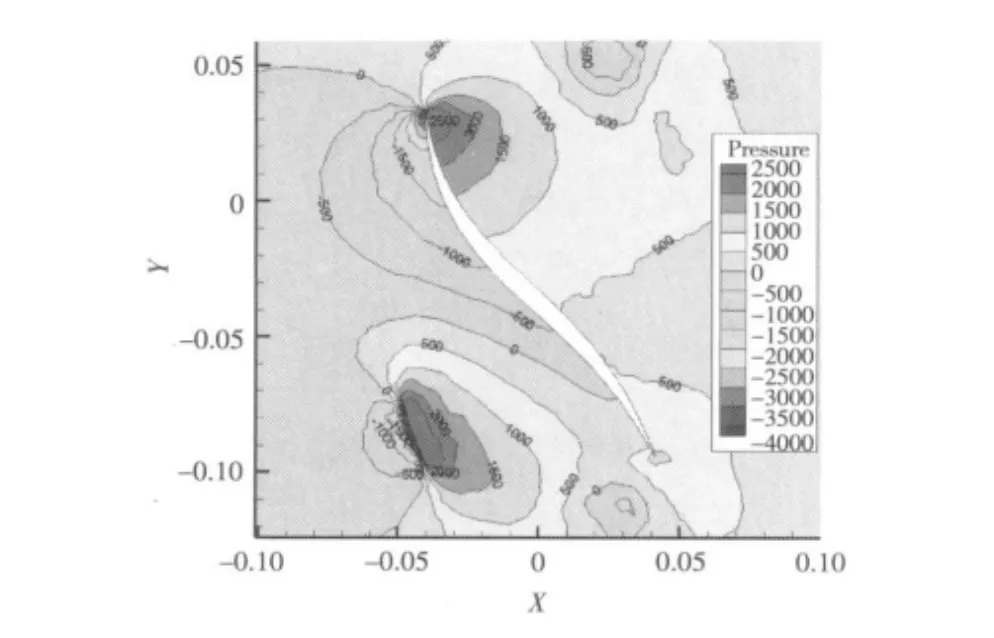
图13 r/R=0.4处压力场——滑移网格Fig.13 The pressure field—sliding mesh of r/R=0.4
2.4.3 尾流场
桨在第一象限运转时,其不同进速系数的尾流场如图14所示。
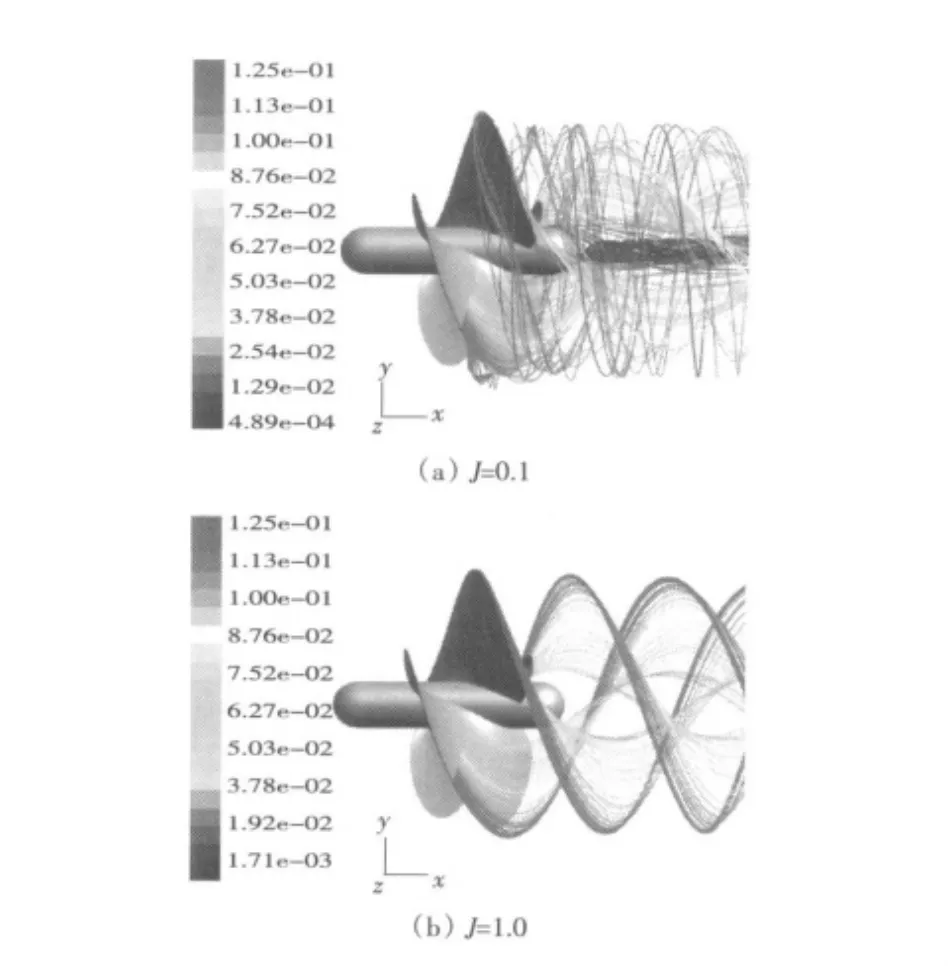
图14 不同进速系数螺旋桨尾流Fig.14 Effect of inlet velocity coefficient of a propeller
由图14可以看出,随着进速系数J的增大,靠近叶梢处尾流的螺距也随之增大,靠近桨毂处尾流的螺距则随之减小。在螺旋桨载荷较强的小进速系数范围内,由于螺旋桨对水流强烈的抽吸作用,使得桨后尾流的直径要明显小于螺旋桨的盘面直径。
3 第三、四象限的拐点和涡
在第二象限和第三象限出现拐点(见图10)时的进速系数,其对应的水流合速度方向近似和叶背(第二象限)或叶面(第三象限)垂直,因此周围流生成了强大的环流涡,如图16所示。

4 结论
根据以上分析可知:
1)桨在第一、四象限运转时的流场非线性较弱,而桨在第二、三象限运转时的流场非线性较强。因此要获取精度较高的敞水桨水动力系数值,需要给出不同的数值求解模式。
2)第二、三象限和第一、四象限求解模式的不同,可概括为以下3点:前者需要更大的定义域;第二、三象限的网格,在桨叶近壁处必须设置多层边界层;处理旋转流场时,第一、四象限可采用MRF,也可采用滑移网格;而第二、三象限都只能采用滑移网格。其中的原因,我们的理解是:MRF不同域之间,如定子和转子之间,不考虑动力学的相互作用。因此在处理强非线性的流场时,MRF会出现结果不稳定等现象,需要用非定常滑移网格模型求解。
3)雷诺数越高,螺旋桨尾流场的湍流强度越大,湍流现象越明显,当试验雷诺数大于临界雷诺数时,其对螺旋桨水动力影响不大。
4)通过数值模拟捕捉到了第二、三象限推力及转矩曲线的拐点,并在其附近发现环流涡现象。通过对环流涡的分析,本文认为环流涡由压力面向吸力面的转移是拐点出现的成因。
5 应用
舰船操纵性和速航性的研究,尤其是各种机动规律的研究,都离不开四象限图谱,现以制动机动为例予以说明。
1)广义的制动机动有倒车法、周期操舵法、倒车摆舵法和改进周期操舵法4种方式。狭义的制动机动指前进中用倒车使舰船停止的操纵方法,这也是本节讨论的课题。
表征制动机动的参数有:XT为从下令倒车开始,舰船沿原航线前进的距离;YT为从下令倒车开始,舰船离原航线横移的距离;制动航迹ST为从下令倒车开始,到舰船的停止前进的航迹;航向变化角φT为从下令倒车开始,到舰船的停止前进的航向变化角;制动航迹tT为从下达倒车口令开始,到舰船的停止前进的时间。
研究舰船制动机动可以用解析的方法,即分段解运动微分方程的方法,也可以用解操纵性方程的方法,本文采用后一种方法。
舰船二阶非线性操纵性响应方程及速度方程如下:


2)求解上述方程,必须知道每一时刻桨的第一象限或第三象限的KT值。以前述AU系列桨为例,其4个象限的KT可用下式描述:
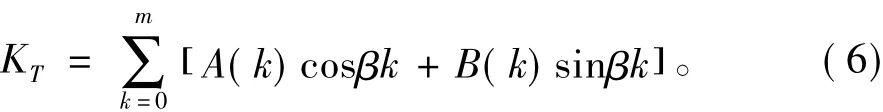
m如取20,能相当精确地表述各象限KT值。文献[9]给出了部分AU桨在上述公式计算时的傅立叶系数值。


图17 系数C1~C5的定义Fig.17 The definition of coefficient C1~ C5
图中,C1为第一象限J=0处的KT值。
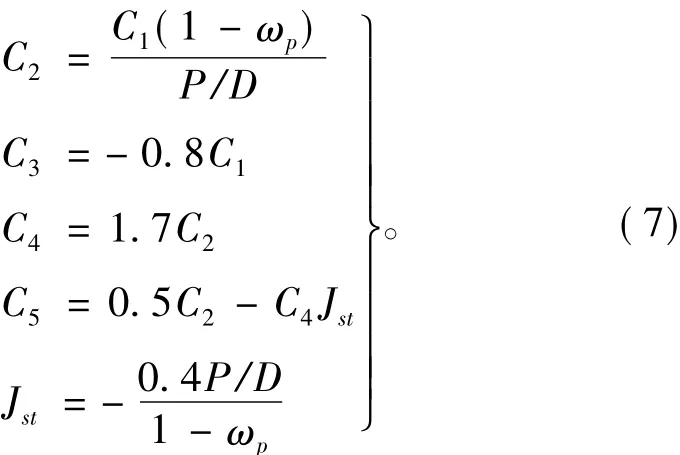
式中:P/D为螺距比;ωp为伴流系数。
将芳村康男公式的结果代入速度方程,经推导可得:


借助上述方程对大型油轮4 m船模的制动机动进行了计算,试验值及计算值对比如图18所示[8]。
上述结果表明,一般操纵性研究,用简化公式表述KT值是可以的。
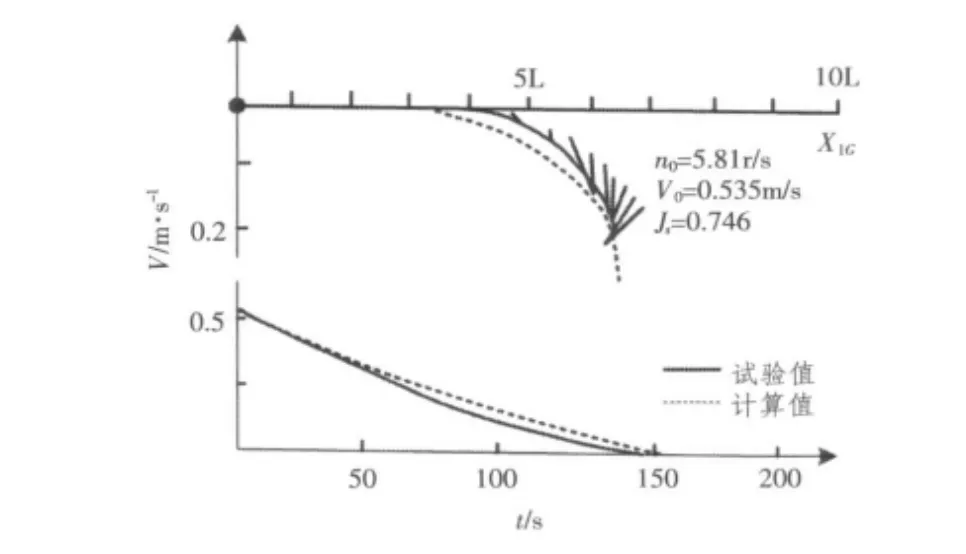
图18 船模制动机动的试验值与计算值Fig.18 Ship model braking maneuver test value and calculated value
[1]奥本明良.5枚羽根プロペヲの后进性能につぃて[J].船舶(日本),1959,32(1):43 -46.
[2]蔡昊鹏,苏玉民,李鑫,等.三维机翼尾涡卷曲的数值模拟[J].大连海事大学学报,2009,35(2):136-140.
CAI Hao-peng,SU Yu-min,LI Xin,et al.Numerical simulation of 3D foil with trailing vortex sheet rollup[J].Journal of Dalian Maritime University,2009,35(2):136 -140.
[3]姚震球,高慧,杨春蕾.螺旋桨三维建模与水动力数值分析[J].船舶工程,2008,30(6):23-26.
YAO Zhen-qiu,GAO Hui,YANG Chun-lei.3D modeling and numerical analysis for hydrodynamic force of propeller[J].Ship Engineering,2008,30(6):23 -26.
[4]叶金铭,熊鹰,王路,等.用RANS方法预报螺旋桨非定常空泡[J].中国造船,2009,50(2):67-73.
YE Jin-ming,XIONG Ying,WANG Lu,et al.Prediction of propeller cavitation using RANS method[J].Ship Building of China,2009,50(2):67 -73.
[5]刘登成,洪方文,张志荣,等.螺旋桨片状空泡的CFD分析[J].舰船科学技术,2009,31(1):43-46.
LIU Deng-cheng,HONG Fang-wen,ZHANG Zhi-rong,et al.The CFD analysis of propeller sheet cavitation[J].Ship Science and Technology,2009,31(1):43 -46.
[6]王超,黄胜,周剑,等.基于周期性边界条件计算螺旋桨的敞水性能[EB/OL].中国科技论文在线精品论文.http://highlights.paper.edu .cn/page_detail.php?id=943.
[7]黄胜,王超,王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J].哈尔滨工程大学学报.2009,30(5):481-485.
HUANG Sheng,WANG Chao,WANG Shi-yang.Application and comparison of different turbulence models in the computation of a propeller's hydrodynamic performance[J].Journal of Harbin Engineering University,2009,(5):481 -485.
[8]野本谦作.船舶操作性和控制及其在船舶设计中的运用[M].中国船舶科学研究中心,1985.20-56.
[9]船用螺旋桨设计参考资料[Z].上海:3203信箱,1978.
The research on numerical simulation of propeller's hydrodynamic performance in four quadrants
LI Li,LIU Ke,LI Chao,XIAO Bing,SHI Ai-guo
(Dalian Naval Academy,DaLian 116018,China)
The propeller's hydrodynamic performance in four quadrants is very important research in the field of maneuverability and rapidity.The paper presents the numerical simulation of the four quadrant hydrodynamic performance of the propeller in open water.The generation of 3D model of propeller is studied and realized.And analysis the calculations from different simulation models and characters of flow field in second and third quadrant,to inflexions of corresponding thrust coefficient curve and circumfluent eddies in first and fourth quadrant.Take brake for example,paper discusses the application of the propeller's hydrodynamic performance in four quadrants.
propeller;hydrodynamic performance;four quadrants;numerical simulation
U664.33
A
1672-7649(2012)07-0008-07
10.3404/j.issn.1672-7649.2012.07.002
2011-08-01;
2011-09-23
李理(1985-),男,硕士研究生,主要从事船舶操纵性及耐波性等研究。

