高速破片入水镦粗变形及侵彻特性有限元分析
沈晓乐,朱 锡,侯海量,周学滨,赵红光
(1.中国人民解放军91439部队,辽宁 大连 116041;2.海军工程大学船舶与动力学院,湖北 武汉 430033)
高速破片入水镦粗变形及侵彻特性有限元分析
沈晓乐1,朱 锡2,侯海量2,周学滨1,赵红光1
(1.中国人民解放军91439部队,辽宁 大连 116041;2.海军工程大学船舶与动力学院,湖北 武汉 430033)
为研究水下接触爆炸产生的高速破片在水中侵彻的阻力特性,采用有限元对典型高速破片入水侵彻过程进行了模拟,计算了破片侵彻的阻力系数,分析了破片墩粗变形规律及其对侵彻阻力的影响,提出了考虑墩粗变形影响的高速破片侵彻阻力及速度计算公式,指出了高速破片的侵彻能力随速度的变化规律。结果表明,初速度大于969~1 187 m/s时破片头部将产生显著变形,并大大影响其侵彻阻力;当破片速度较小时,入水侵彻深度随初始弹速的增大而增大,当破片速度达到某一临界值以后,侵彻深度将随初始入射速度的增大而逐渐减小。
爆炸力学;高速破片;侵彻;防护水舱;侵彻阻力
0 引言
水下接触爆炸的2个主要毁伤元素是冲击波和高速破片,其中高速破片初始速度在2 000 m/s左右具有很强的穿甲破坏能力。为抵御高速破片的侵彻,大型舰船主要通过设置隔离水舱或重油舱衰减吸收高速破片的动能,以减小其对后续防护结构的穿甲破坏。
关于水下弹道特性的研究,20世纪70年代矶部孝等曾对弹速在500~800 m/s下弹体的入水及跳弹,水中弹体侵彻能力等问题进行了大量的实弹试验,并提出了不同弹型侵彻能力的一系列经验公式[1]。近年来,人们针对速度小于400 m/s的长杆型弹体的减阻及超空泡问题开展了大量研究[2-4]。徐双喜等采用Fluent计算了初速1 600 m/s左右的水中立方体弹的侵彻阻力系数,拟合出与雷诺数相关的阻力系数曲线[5]。针对速度在2 000 m/s的高速破片入水及侵彻特性问题还未见相关报道。
本文采用MSC/Dytran对速度在1 000~2 500 m/s的立方体破片的入水及水中侵彻过程进行了数值模拟,计算了破片水中侵彻的阻力系数,分析了高速破片的水中侵彻特性,分析了破片墩粗变形规律及其对侵彻阻力的影响,提出了考虑墩粗变形影响的高速破片侵彻阻力及速度计算公式,指出了高速破片的侵彻能力随速度的变化规律。
1 有限元模型
1.1 计算算法
采用MSC/Dytran中的拉格朗日-欧拉耦合计算方法,模拟高速破片由空气垂直入水及其在水中的侵彻过程(见图1)。空气和水介质采用欧拉网格进行描述;高速破片为立方体形,考虑到大型舰船外板典型厚度在15~20 mm,故将其边长定为16 mm,采用拉格朗日网格进行描述。
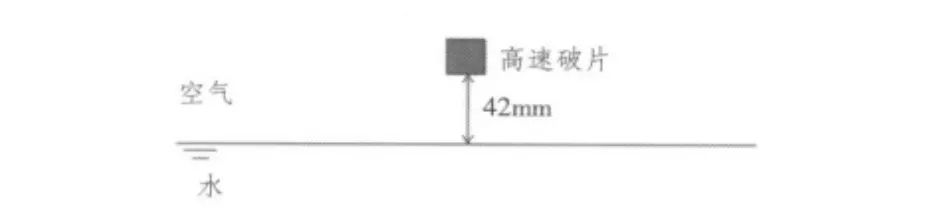
图1 高速破片初始位置示意图Fig.1 Schematic of the high velocity fragments'position
1.2 材料模型

高速破片材料采用双线性弹塑性本构模型,材料的应变率效应由Cowper-Symonds模型描述,动态屈服强度式中:σ0为静态屈服强度;Eh为应变硬化模量;εp为有效塑性应变;为等效塑性应变率;D和n为常数,对于低碳钢D=40.4/s,n=5;材料失效模型采用最大塑性应变失效。计算中,假设高速破片的材料为低碳钢,其材料参数如表1所示。

表1 高速破片材料参数Tab.1 Model constants of high speed fragment
假设水介质为非线性可压缩流体,其状态方程为p=a1μ +a2μ2+a3μ3+(b0+b1μ +b2μ2+b3μ3)ρ0e。 (2)式中:p为压力;a1,a2,a3,b0,b1,b2,b3为材料常数;μ=ρ/ρ0-1;ρ0为初始密度;e为质量比内能。
假设空气介质为无粘性的理想气体,状态方程为

式中:γ为绝热指数;ρ为密度;e为质量比内能。计算中水及空气的材料参数分别如表2和表3所示。

表2 水的材料参数Tab.2 Model constants of water

表3 空气介质的状态参数Tab.3 Model constants of air
2 计算结果及分析
2.1 墩粗变形特性
高速破片在初始入水时刻,将产生巨大的压力,而使头部发生墩粗变形,其典型变形形态如图2所示。由于头部墩粗,破片水中侵彻时迎水面积增大,图3是破片头部迎水面积随初始弹速的变化曲线,其中墩粗率η=A/A0-1,A0为初始迎流面积,A为墩粗变形后面积。
由图3可知,当初始弹速小于1 000 m/s时,破片头部无明显墩粗;当弹速大于1 200 m/s时,破片头部墩粗显著增加,头部迎流面积近似随初始弹速平方的增大而增大。其主要原因是,破片入水初始阶段受到的侵彻阻力主要是水的惯性压力,假设水为Bernoulli方程的不可压缩的无粘性流体,根据Tate-Alekseevskii[6]弹体侵彻模型,则破片受到的压力p可表示为
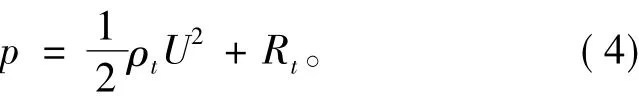
式中:ρt为靶体,即水的密度;U为破片的侵彻速度,近似等于初始破片速度;Rt定义为与靶体材料的剪切强度相关的抗侵彻强度,对于水,可取Rt=0。
对于高速破片入水侵彻问题,p随弹速平方的增大而增大,当p大于破片材料的动态抗压屈服强度σd时,破片开始发生墩粗变形。对于低碳钢材料,σd约为静态屈服强度的2~3倍。因此,当初始弹速大于969~1 187 m/s时,低碳钢材料破片开始发生显著的墩粗变形。

2.2 侵彻阻力特性

图4 与间的变化关系Fig.4Relationship betweenand v—
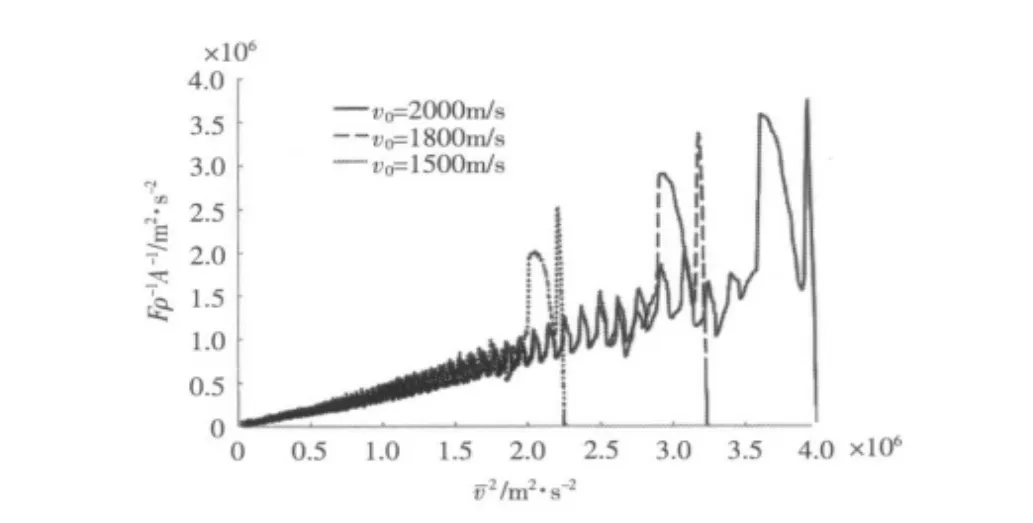
图5 F/(ρA)与间的变化关系Fig.5Relationship between F/(ρA)and
由图4可知,破片入水初始时刻,破片的加速度由0迅速增大。其原因是水界面初始时刻并未受到扰动,由于受到破片的撞击,将分别向水介质和破片中产生压力波,破片头部速度迅速减小,破片动能转化为变形能和水中的激波能。当压力波传播到破片尾端时,平均加速度将达到最大,此后将反射成稀疏波,平均加速度略为减小,当稀疏波传播到弹头后,将产生新的压缩波,平均加速度再次增大。如此反复,直至破片平均速度小于水中压力波速(约为1 500 m/s)。此后,水中压力波脱离破片头部,破片在水中形成稳定侵彻,破片阻力明显减小,平均加速度近似与速度的平方呈线性关系减小(见图5)。
文献[1,8]认为破片在水中运行过程中阻力的大小与速度的平方成正比,并认为阻力系数Cd为常数,由此得到破片的侵彻阻力F,侵彻距离L及侵彻速度v的计算公式:

式中:v0为初速度;v1为剩余速度;Cd为阻力系数;A为迎流面积;ρ为水密度。式中并未考虑破片侵彻过程中破片迎流面积变化的影响。
考虑水中压力波脱离破片头部后的稳定侵彻阶段,忽略侵彻阻力的波动现象,可得破片侵彻的阻力系数(F/(ρAv2)的平均值)随初始弹速v0的变化关系如图6所示。由图可知,当v0<1 200 m/s时,破片侵彻的阻力系数近似保持不变;当v0≥1 200 m/s时,破片侵彻的阻力系数随初始弹速的增大而迅速增大。由于流体黏性而引起的阻力系数Cd并不随初始弹速的变化而变化,而当初始弹速大于969~1 187 m/s时,低碳钢材料破片开始发生显著的墩粗变形。因此,破片侵彻阻力系数的变化主要由破片的墩粗变形引起的。

图6 F/(ρAv2)平均值与v0间的变化关系Fig.6 Relationship between average of F/(ρAv2)and v0
假设由于头部墩粗变形而引起的阻力增加的影响系数为Ca,则破片的侵彻阻力

侵彻距离L和侵彻速度v分别为:

式中:Cd可近似取v0<1 200 m/s时稳定侵彻阶段F/(ρA0ν2)的平均值;Ca可近似取稳定侵彻阶段F/(CdρA0ν2)的平均值。由数值计算结果拟合后可知,对于低碳钢立方体破片
表4为不同初速下,破片侵彻深度的有限元计算结果和未考虑破片墩粗变形影响(式(5))及考虑破片墩粗变形影响(式(6))的计算结果。由表4可知,考虑破片墩粗变形影响后,计算偏差大大减小。
2.3 破片速度衰减规律及侵彻能力
图7显示了破片速度随时间的变化情况。由图可以看出破片入水早期0~0.5 ms,速度能快速衰减;随着时间的推移,到后期1~2 ms时速度衰减放缓。这是因为侵入液舱之后,由于速度很高,破片头部接触区域的液体表现出巨大的惯性效应,破片动能很快转化为周围液体的动能;到入水后期,随着破片速度的降低,破片与头部液体间的速度梯度下降,水的惯性效应减小,破片加速度降低,从而使破片速度衰减放缓。
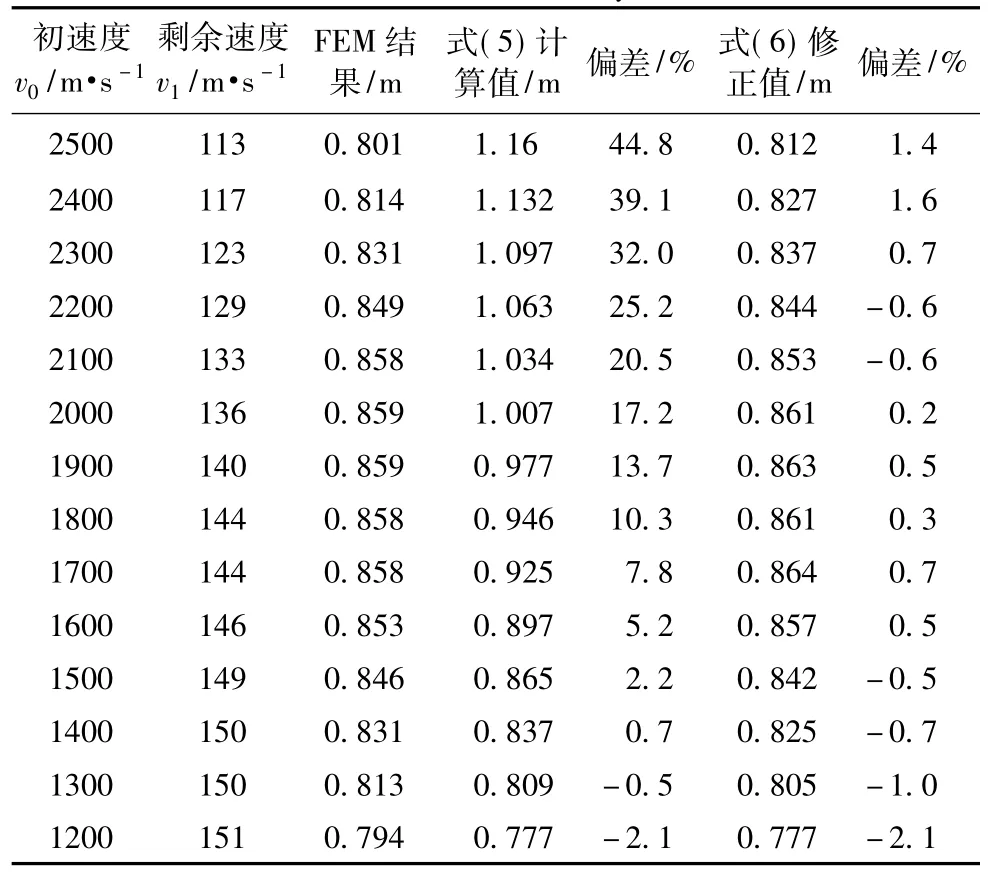
表4 偏差分析Tab.4 Error analysis

图8为采用有限元分析的剩余速度为100 m/s时破片的侵彻深度随初速度变化情况。由式(5)和式(6)可知,破片入水侵彻深度L与破片的速度呈对数关系,在破片形状、质量、剩余速度一定的条件下,侵彻深度应随初始速度的增大而增大。但是图中结果表明破片的侵彻能力并未随速度增加而增加,当速度达到1 900 m/s后,破片的侵彻深度反而下降。由破片的墩粗变形分析可知,破片入水瞬时在弹体内部形成压缩波,当速度达到969~1 187 m/s时压缩应力超过了弹体材料的动态强度,使破片产生墩粗塑性变形;且随着破片入水速度的增加墩粗变形量加大,见图3。因为破片的侵彻深度与迎流面积呈反比,所以当由于墩粗变形引起的侵彻深度下降的增量大于速度增大而引起的侵彻深度增加的增量时,破片的侵彻能力开始降低。
3 结语
1)高速破片入水侵彻初始时刻将受到水的惯性力作用而形成压缩波。对于低碳钢材料弹体,当初始弹速大于969~1187 m/s时,压缩波强度将大于材料的动态屈服强度而使破片发生墩粗变形;
2)随着初始弹速的增加,破片的墩粗变形将大大影响其侵彻阻力;
3)高速破片入水初期,速度衰减很快;且初始弹速越大,速度衰减越明显;到后期速度衰减放缓;
4)当弹速较小时,高速破片的入水侵彻深度随初始弹速的增大而增大,当速度达到某一临界值以后,侵彻深度L随初始弹速的增大而逐渐减小。
[1]矶部孝.水下弹道的研究[M].北京:国防工业出版社,1983.
[2]顾建农,张志宏,范武杰.旋转弹丸入水侵彻规律[J].爆炸与冲击,2005,25(4):341-349.
GU Jian-nong, ZHANG Zhi-hong, FAN Wu-jie.Experimental study on the penetration law for a rotating pellet entering water[J].Explosion and Shock Waves,2005,25(4):341-349.
[3]熊天红,易文俊,吴军基,等.水下高速射弹超空泡流特性分析[J].火炮发射与控制学报,2008,(4):6-9.
XIONG Tian-hong,YI Wen-jun,WU Jun-ji.Analysis on super-caviting flow characteristics of underwater high-speed projectile[J].Journal of Gun Launch and Control,2008,(4):6-9.
[4]蒋增辉,于开平,张嘉钟,等.水下航行体通气超空泡形态及阻力特性试验研究[J].工程力学,2007,24(4):152-158.
JIANG Zeng-hui,YU Kai-ping,ZHANG Jia-zhong,et al.Experimental research on shape and drag characteristics of ventilated super-cavity on under-water bodies[J].Engineering Mechanics,2007,24(4):152 -158.
[5]徐双喜,吴卫国,李晓彬,等.破片在防护液舱内运行规律研究[A].第三届全国舰艇抗冲击技术交流会会议论文[C].哈尔滨:哈尔滨工程大学.
[6]TATE A.A theory for the deceleration of long rods after impact[J].J.Mech.Phys.Solids,1967,15(6):387 -399.
[7]王永虎,石秀华.入水冲击问题研究的现状与进展[J].爆炸与冲击,2008,28(5):276-282.
WANG Yong-hu,Shi Xiu-hua.Review on research and development of water-entry impact problem[J].Explosion and Shock Waves,2008,28(5):276 -282.
[8]VARAS D,LO'PEZ-PUENTE J,ZAERA R.Experimental analysis of fluid-filled aluminium tubes subjected to highvelocity impact[J].InternationalJournalofImpact Engineering,2009,36(1):81-91.
Finite element analysis of underwater high velocity fragment mushrooming and penetration properties
SHEN Xiao-le1,ZHU Xi2,HOU Hai-liang2,ZHOU Xue-bin1,ZHAO Hong-guang1
(1.No.91439 Unit of PLA,Dalian 116041,China;2.College of Naval Architecture and Power,Naval University of Engineering,Wuhan 430033,China)
In order to explore the under water resistance of high velocity fragment produced by under water contact explosion.Finite element analysis was carried out to simulate the process of high velocity fragment penetrating water.The resistance coefficient was found out.the mushrooming rule due to high velocity and its influence on the penetration resistance ware discussed.The penetration resistance and velocity formulas which sufficiently considering the affect of altering in front face were brought forward.rule of penetrate capacity according the velocity change was also pointed out.Results indicate as follows:Initial velocity excess 969 ~ 1187 m/s,the mushrooming was definite,it will affect the resistance sufficiently.When the initial velocity is low,the penetrate depth will increase with initial velocity,when the fragment velocity achieve to some critical value,the penetrate depth will decrease with initial velocity increase.
explosion mechanics;high velocity fragment;penetrate;protecting water cabin;penetrating resistance
O353.4
A
1672-7649(2012)07-0025-05
10.3404/j.issn.1672-7649.2012.07.005
2011-07-15;
2011-10-17
沈晓乐(1985-),男,助理工程师,主要研究方向为舰艇抗爆抗冲击。

