一种基于MATLAB的浮球姿态视觉检测系统
邹益民
(南京铁道职业技术学院 通信信号学院,南京 210031)
0 引言
液浮陀螺中浮球的静平衡直接关系到陀螺仪的精度与综合性能,在产品生产与调试过程中是质量控制的关键环节。由于对浮球静平衡的指标有严格要求,常规的接触式检测方式难以奏效。实践中采取将浮球置于一定密度的仪表液之中,使其呈自由悬浮状态,通过测量其悬浮姿态的变化来确定其轴向静平衡状况。考虑到该浮球由一个圆球及贯通球心的一条轴孔组成,故检测的目的实际是确定轴孔相对于参考坐标系的方向。若采用光学准直仪等类似的光学方法进行检测则对测试设备提出了较高要求,本测试系统采用基于数码相机的简易视觉检测方式:通过相机摄取浮球的姿态信息,再借助软件与必要的人机交互即可完成对浮球空间姿态的非接触测量。
1 检测系统组成及工作过程
本检测系统由测试台、恒温冷柜、测试方瓶、数码相机、计算机及相关软件组成。测试台用于安放计算机、打印机等设备,提供测试工作台案;恒温冷柜用于降低测试方瓶中仪表液的挥发,并保证其密度满足测试要求,其表面透明,可直接对内部测试方瓶中的浮球进行拍摄;测试方瓶是承载测试用仪表液与浮球的透明容器;数码相机用于透过测试方瓶摄取浮球的平衡状态;计算机及相关软件用于对数码相机摄取的图像进行交互式处理,最终完成对浮球平衡位置的检测。
视觉检测技术是通过非接触手段进行目标物体测量的一种常用方法。一般而言,利用二维图像信息估计物体的三维参数需要采用多个视图的立体视觉方法,但若物体的特征模型已知,则基于单视也能进行物体三维位置估计。其中一类是利用物体与其图像之间的点[1]、线[2]对应关系求解其三维位置,另一类则是基于物体中常有的圆形、球形特征估计其三维位置[3]。本文给出一种基于圆与球特征的浮球轴向姿态视觉检测方法[4]:若已知球体、轴孔的形状参数及相机焦距,则可用两种方法估计所需的方向参数:1)直接估计轴孔圆形端面法向量的方向余弦;2)分别估计球体中心与轴孔圆形端面中心的三维位置,进而计算出所需的端面法向量方向余弦。显然,两种方法可相互验证。
2 检测算法原理
2.1 基于空间圆特征的物体三维位置估计
取空间圆的法向量指向相机方向,建立如图1所示的图像坐标系xyz及相机坐标系xcyczc。若相机焦距为e,相机光心与投影图像形成一构造圆锥,该构造锥将通过空间中的圆特征,而角点位于相机光心。

图1 空间圆与其图像点的投影关系
若圆特征在图像平面的投影椭圆可表示为:


式中:

将式(2)的构造圆锥方程由图像坐标系经坐标变换T0变换至相机坐标系,则有:XTAX=0。

取坐标变换T1,将方程(2)简化为下述形式的中心圆锥方程:


可以证明[5]: 是矩阵A的特征值,而[limini]可由相应的特征矢量求得。
设截平面lX+mY+nZ=p与(6)式所示的中心圆锥截交线为圆。作旋转变换T2,使新坐标系X'Y'Z'的Z'轴与圆截平面正交,这样,截交面位于Z'=p,截交线方程为:
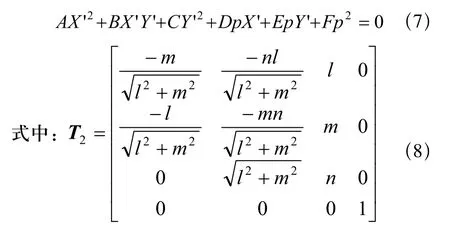
因截交线是圆,则有:A=C,B=0,且l2+m2+n2=1,整理可得:
1) 若 ˜1< ˜2,

事实上,中心锥圆形截交面方向余弦[l m n]T即为圆特征平面法向方向余弦。
由式(7),再由A=C,B=0,设圆半径为r,则还可求得截交圆心为:

2.2 基于球特征的物体三维参数估计
对于中心位于x0, y0, z0, 半径为R的3D球面,有:

从相机坐标系原点Oc(0, 0, 0)向其作切线,形成封装锥体为[5]:

采用与上节类似的方法获取中心锥,则中心圆锥方程可简化为:


图2 空间球与其图像点的投影关系
比较式(9)即可得球心坐标:
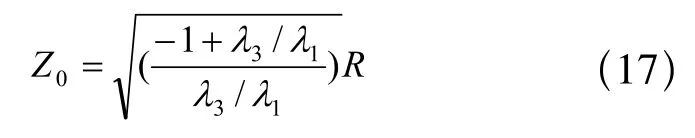
类似地,可使用式(7)中T1的旋转部分将所求球心坐标由XYZ坐标系变换至相机坐标系。
3 仿真计算
考虑如图3所示的空间球体及中心轴孔形成的圆形端平面的估计问题。定义世界坐标系为xwywzw,不失一般性,设球体中心位于(0, 0, 22),半径R=25;轴孔端面构成的空间圆特征中心位于(0, 0, 0),半径为r=6.8。相机焦距e=22,点距为0.02,单位均为mm,再设相机坐标系xcyczc与世界坐标系xwywzw的变换关系为:

图3 算法的仿真示例

计算光心与球体及圆端面形成的构造锥及其投影椭圆方程,并对两个投影椭圆分别进行采样,样本点取30个,再加入零均值,方差为0.1-2pixel范围的高斯噪声,重复50次,计算估计所得的球心、圆心与理论值的均方根误差,同时计算估计所得端面法矢量、中心线(球心与圆心连线)方向矢量与理论值的均方根误差角,结果如图4所示。由图可见,本文所述估计方法对于估计球体姿态是有效的。同时,采用基于球心与圆心连线的中心线估计比直接采用端面圆法向量估计的结果具有更小的误差。这主要是由于较小的端面圆投影图像更易受到噪声干扰,造成估计误差相对偏大。
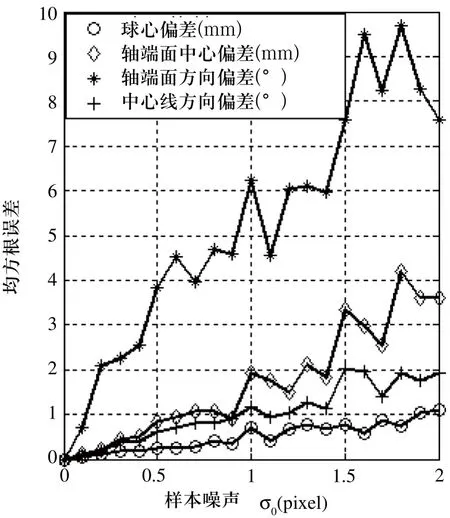
图4 样本点噪声与估计误差
4 软件程序功能简介
MATLAB是MathWorks公司开发的“演算纸”式的程序设计语言,它提供了强大的矩阵运算和图形处理功能,几乎在所有的工程计算领域都提供了准确、高效的工具箱,并可通过m函数文件扩展其算法功能。
本程序首先借助MATLAB灵活的GUI函数实现所需的图形用户界面,其次充分利用MATLAB丰富的图像处理功能以实现图像的打开、裁剪、灰度化、中值滤波、边缘检测、Radon直线检测等功能,再使用自编的函数实现图像中的圆/椭圆特征检测及前文中所述的空间球体及中心轴孔的位置估计算法,从而大大简化了程序设计。测试程序的功能菜单框图如图5所示。
1)“文件”菜单:
“打开图像”子菜单:打开拍摄的图像文件,文件格式可是BMP或JPG;
使用下述MATLAB代码可完成图像文件的选择与读取:
[FileName PathName]= uigetfile('*.bmp;*.jpg');
RGB=imread(strcat(PathName,FileName));
“退出”子菜单:退出图像检测软件。
2)预处理”菜单:
“裁剪与灰度化”子菜单:将打开的RGB格式图像文件裁剪至适当大小,以加快程序处理速度。同时完成图像文件的灰度化。
使用下述MATLAB代码可由用户对图像文件进行适当的剪切,并将剪切后的RGB彩色图象变换成灰度图像:
RGB_Crop=imcrop(RGB);
GRAY=RGB2gray(RGB_Crop);
“提取边界”子菜单:增强图像的边缘信息(必要时首先对图像进行中值滤波),便于用户手动选择样本点。
使用下述MATLAB代码可对剪切后的灰度图像完成中值滤波,并基于LOG算法取得图像的边缘图二值图:
GRAY=medfilt2(GRAY,[7,7]);
BW=edge(GRAY,'log',[]);
3)“直线检测”菜单:
“Radon检测”子菜单:采用Radon算法对浮液水平面进行检测,以校正相机歪斜的影响。
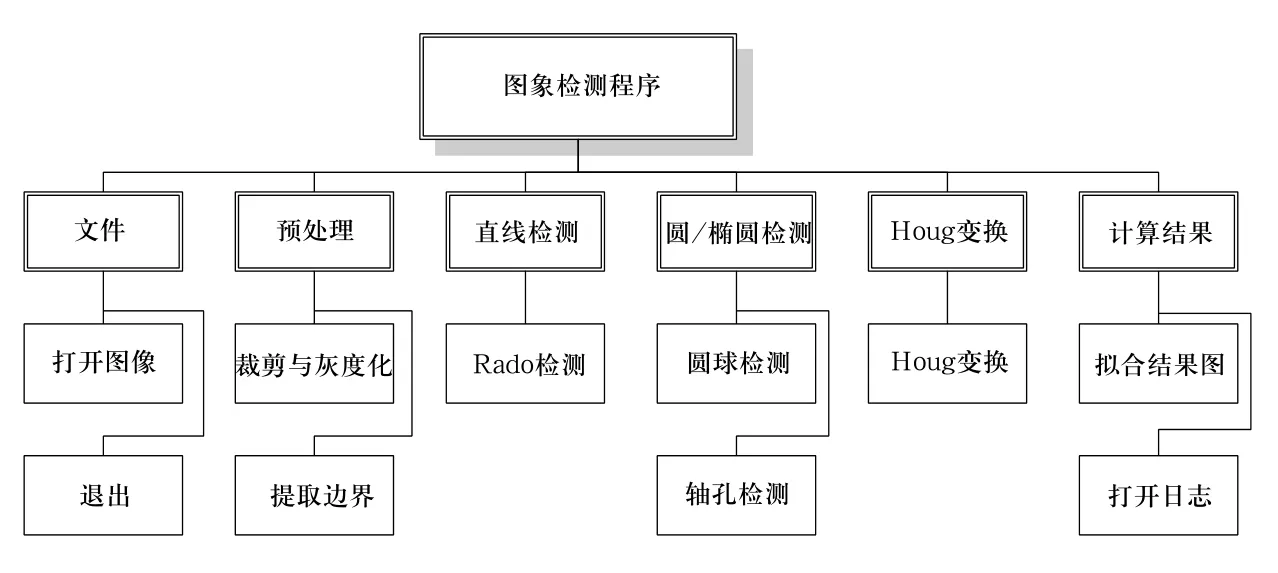
图5 程序功能菜单框图
使用下述MATLAB代码可实现对边缘图像的Radon变换,在变换后的图像中搜索最大值点,即可鲁棒地获得对水平面的位置检测,最后实现对相机歪斜的相正:
[R,xp]=radon(BW,theta);
4)“圆/椭圆检测”菜单:
“圆球检测” 子菜单:利用手工方法,标定浮球的投影椭圆轮廓上若干样本点,使用基于几何距离的非线性最小二乘法获得投影椭圆轮廓[6];使用下述MATLAB代码建立一种交互机制,供用户使用手工方式对投影椭圆上的若干轮廓点进行标示,以便后续基于最小二乘法对投影轮廓进行拟合:[X Y]=getpts;
“轴孔检测” 子菜单:利用手工方法,标定浮球的中心轴孔投影椭圆轮廓上若干样本点,使用非线性最小二乘法获得投影椭圆轮廓;
处理方式与“圆球检测”相似。
5)“Hough变换”菜单:
“Hough变换”子菜单:对上述圆球、轴孔的检测结果利用随机Hough变换(RHT)[7]进行拟合处理,以降低对图像点取样的随机性。
6)“计算结果”菜单:
“拟合结果图”子菜单:将上项检测的结果迭加在原图上,以观察检测的结果是否满足要求;
“浮球姿态计算”子菜单:根据上述检测出的投影轮廓及第2节算法,对浮球姿态进行估计,并将计算结果存入日志;
“打开日志”子菜单:显示日志文件中的相关信息。
5 结论
文中讨论了一种基于单视图像对空间给定球体与圆特征进行三维位置估计的算法。利用浮球形体中存在的球及圆特征,采用上述算法,即可由图像信息估计出浮球及其中心轴孔的空间姿态。使用MATLAB提供的强大的图像处理工具箱及可视化界面,加之其便捷的程序扩展能力,从而可方便地实现所需的桌面视觉系统的功能,实现对浮球姿态的非接触测量。应用结果表明,该系统可用于对液浮陀螺中浮球的静平衡状态进行有效检测,从而有助于提高陀螺仪的精度与综合性能。
[1] Horaud R, Conio B, Leboulleux O. An analytic Solution for the perspective 4-Points problem [J]. Comput. Vision,Graphics Image Processing, 1989; 47:33-44.
[2] Haralick R M. Solving Camera Parameters from the Perspective Projective Projection of a Parameterized Curve[J]. Pattern Recognit, 1984; 17(6): 637-645.
[3] Safaee-Rad R, Tchoukanov I, Smith K C, et al. Threedimensional location estimation of circular features for machine vision [J]. IEEE Trans. on Robotics and Automation, 1992; 8:624-640.
[4] 邹益民, 汪渤. 基于单视图像的球体姿态估计[J]. 电子与信息学报, 2007, 29(8): 1826-1828.
[5] Mosnat E. Problemes de Géométrie Analytique[M]. 3rd Ed, Paris: Vuibert, 1921.
[6] Spath H. Orthogonal distance fitting by circles and ellipses with given area [J]. Comput. Stat. 1997; 12: 343-354.
[7] Xu L, Oja E. Randomized Hough transform: basic mechanisms, algorithms and computational complexities[J]. Computer Vision Graphic Image Process: Image understanding, 1993, 57(2): 131-154.

