下肢外骨骼康复机器人的自适应控制研究

陈贵亮，李长鹏，刘更谦

（河北工业大学 机械学院，天津 300130）

0 引言

我国和世界上许多国家一样正在进入老龄化。大量老龄人患有偏瘫症状的脑血管疾病，中国的发病率稍偏高于世界平均水平，属于脑卒中高发地区之一，而且在年龄上呈现出年轻化趋势[1]。

70%～80%的脑卒中患者会留有不同程度的下肢运动障碍。临床医学证明，脑卒中偏瘫患者除了手术和必要的药物治疗以外，早期的运动康复治疗能够明显提高患者肢体运动功能的最终恢复程度。神经康复医学理论证明：中枢神经系统具有高度可塑性。以此为依据，通过将计算机控制技术、康复医学和机器人相结合，将医师从传统的“多对一”康复训练模式中解放出来，为患者提供科学的、安全的和高效率的康复训练。因此，康复机器人技术已成为国内外研究的热点。

文献[2～4]中阐述了鲁棒自适应控制应用于不确定性机器人轨迹跟踪问题的研究成果，但仍存在着控制器结构复杂、计算量大和稳定性差等问题。将预先获得的近似模型作为标称模型用于控制器设计，能够减轻计算机运行负担，缩短运算时间，实现在线实时控制。文献[5～7]中的控制方法并没有考虑未建模动态和环境不确定因素。

本课题组研发的下肢外骨骼康复机器人系统具有强耦合非线性动态特性和参数不确定的特征。本文中根据其动力学模型特征和康复训练控制要求，采用的变结构鲁棒自适应补偿控制器不需对系统的未知参数进行估计，通过引入非线性阻尼项来消除未建模动态、未知有界扰动和参数不确定性的影响。将两个相互独立的控制器相结合可以达到对这类系统实时、精确的控制目的。利用Lyapunov理论对其进行的分析和仿真实验研究证明了系统的稳定性。

1 下肢外骨骼康复机器人系统

下肢外骨骼康复机器人虚拟样机及其右腿结构简图如图1所示。

图1 下肢外骨骼康复机器人虚拟样机及其右腿结构简图

外骨骼机器人大腿杆绕点O1转动，长度为l1，与竖直垂线之间的夹角为髋关节角q1；小腿杆绕点O2转动，长度为l2，与大腿杆延长线的夹角为膝关节角q2。根据以上下肢外骨骼康复机器人系统的物理模型，可为其建立完整的拉格朗日动力学方程为：

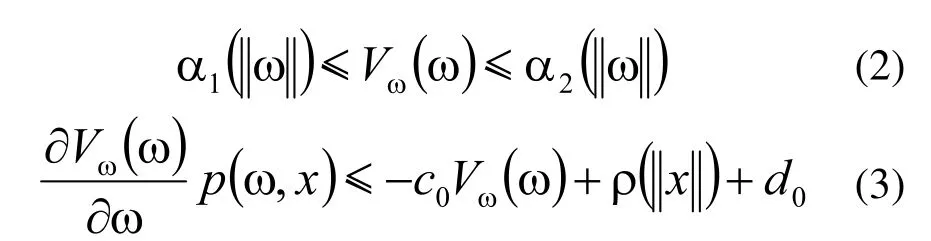
这里，a1, a2为类函数，c0>0, d0≥0为常数。为了不失一般性，我们假设r(·)有这样的形式：r(h) =h2r0(h2)，其中，r0是一个非负的光滑函数。否则，我们可以将r表示为是一个充分小的实数。

为了描述未建模动态对控制系统的影响，我们使用一个动态信号r，定义为：

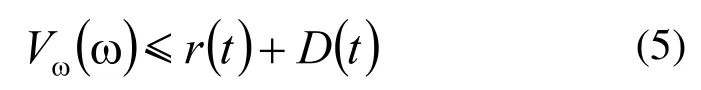
且对于所有t≥0，式（5）成立。对于所有t≥T0≥0，存在一个有限常数T0，使得D(t)=0。

由式（2）和式（5）得：

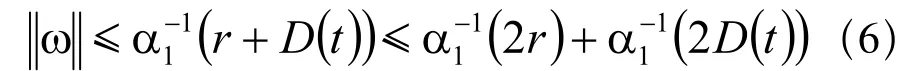
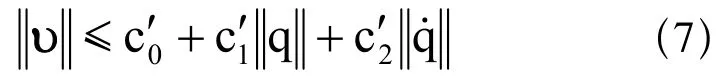
j'(w, q, u, t)为系统中不确定非线性以及和未建模动态w及q、u、 有关的不确定性，j'和p都是未知的非线性Lipschitz连续函数，并且满足：

由式（6）～式（8）得：

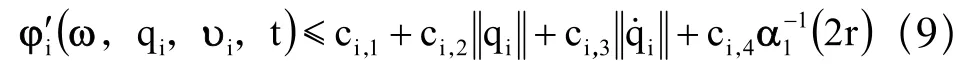
T负为负载作用等效到关节的等效力矩，可由力传感器和其到相应关节的距离获得；非线性摩擦T摩＝［F1F2]T可表示为[9]：

式中，Fs，Fc分别为未知的静摩擦力和动摩擦力，正常数ds、dc分别为其上界，i=1, 2。

根据以上的分析推导，为减轻系统计算负担，对下肢外骨骼康复机器人系统的不确定性进行参数分离得：

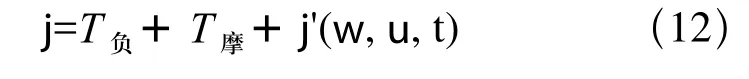
2 控制器设计及稳定性分析

下肢外骨骼康复机器人系统的标称动力学模型为：）

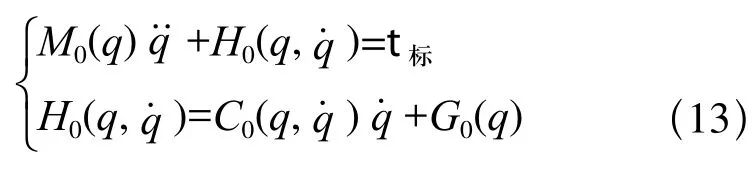
根据文献[10]中的计算力矩控制设计方法，则系统的标称输入力矩和输入加速度矢量分别为：

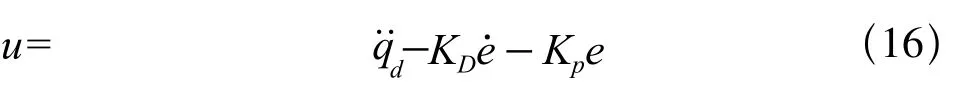
因此外骨骼康复机器人系统的标称力矩输入为：

由式（13）和（17）得误差方程：

根据以上可知，这是基于机器人标称模型的前馈加反馈控制，前馈的作用在于抵消各关节的耦合，反馈则用于补偿跟踪偏差。式（18）表明如果适当选择反馈增益KD，Kp轨迹误差可以渐近稳定收敛于0。

将式（17）带入式（1）得：

将式（20）带入实际模型式（1）有：

上式表明，如果通过适当地选择补偿控制器，并使计算出的补偿值能趋近于系统的不确定项，能够使下肢外骨骼康复机器人的实际系统达到期望的指标。

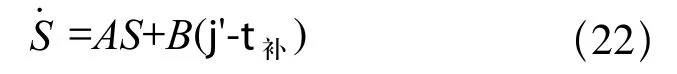
已知A为稳定矩阵，则存在一个正定矩阵P使下列Lyapunov方程有解：ATP+PA=-Q，其中，QR2×2是给定的正定对称矩阵。

针对式（22）给出下列变结构鲁棒自适应控制算法[11]：

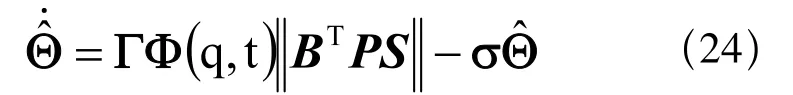
其中，对角阵 为参数自适应修正速率，s为系统特性设计给定的修正参数，用于增加系统的鲁棒性。

选取Lyapunov函数为：

将式（25）对时间求导得：

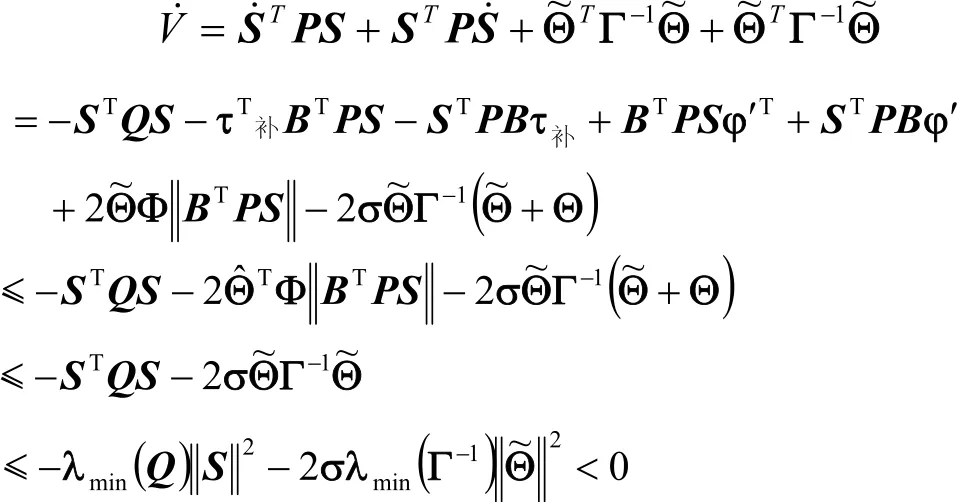
通过上面的推导得知Lyapunov函数满足以下条件：

根据Lyapunov定理，下肢外骨骼康复机器人的实际系统达到期望的指标，即全局指数稳定。

3 仿真实验

采用课题中下肢外骨骼康复机器人的数学模型用于仿真实验，以验证本文算法的可行性和有效性。以男性身高175mm，体重70kg为康复训练对象，人体和外骨骼结构参数为大、小腿质量分别为6.72kg和2.94kg，大腿杆质量和长度为m1=1.5kg，l1=0.5m，小腿杆质量和长度为m2=1kg，l2=0.4m，杆上相应的传感器到髋、膝关节的距离分别为0.25m和0.2m。则式（1）中的M0(q)、C0(q, q.)、G0(q)具体表达式为：

利用Matlab/Simulink仿真工具箱并用M文件编写S函数模块进行仿真，先对美国斯坦福大学开发的OpenSim软件[12]中提供的人体步态数据进行拟合，获得右髋、膝关节的跟踪轨迹为:

尽管系统存在未建模动态和扰动等，采用两个独立控制器的联合作用后，实际轨迹能够快速跟踪期望轨迹，开始时小幅度地跟随曲线趋势的变化，存在的位置误差被控制在人体关节运动的安全范围内，并且保证指数意义下渐近稳定、全局收敛一致有界。

图2 2s步态周期髋关节角度轨迹

图3 2s步态周期膝关节角度轨迹

4 结论

分析证明，本文针对本课题组研发的下肢外骨骼康复机器人系统动力学模型的非线性，所提出的两个相互独立的控制器共同作用，基于标称模型的计算力矩控制器通过高频采样，实现有偏差跟踪的控制方法，可以减轻计算机负担，保证系统的实时性。利用变结构鲁棒自适应控制构造的补偿控制器，弥补由于未建模动态、外部有界扰动和非线性不确定项等造成的影响，通过引入的滑动方程使系统状态在有限时间内到达切换面，开始存在的位置误差在人体关节运动的安全范围内，符合康复医学的要求。仿真实验研究结果表明，本文提出的控制策略在跟踪速度和精度上都具有明显优势。

[1] 南登. 康复医学[M]. 人民卫生出版社, 2005: 1-35.

[2] Ortega R, Spong M W. An adapative motion control of rigid robot.Proc IEEE Conf Decis Control[C], Austin, TX, USA,1988. 1575-1584.

[3] Jun-ichi Imura, Toshiharu Sugie, Tsuneo Yoshikawa.Adaptive robust control of robot manipulatorw-theory and experiment [J], IEEE Trans Automat Control, 1994, 10(5):705-710.

[4] 代颖. 不确定性机器人的鲁棒自适应控制方法研究[D].西安: 西安交通大学电信学院. 1998.

[5] Lin Wei, Qian Chunjiang. Adaptive control of nonlinearly parameterized systems: the smooth feedback case [J]. IEEE Trans Automat Contr, 2002, 47(8): 1249-1266.

[6] Riener R,Lunenburger L,Jezernik S,et al. Patientcooperative strategies for robot-aided treadmill training:first experimental results [J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2005, 3(13):380-394.

[7] Jezernik S, Colombo G, Morari M. Automatic gait-pattern adaptation algorithms for rehabilitation with a 4-DOF robotic orthosis [J]. IEEE Transaction on Robotics and Automation, 2004, 20(3):574-582.

[8] Jiang, Z P, Praly L. Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties[J].Automatica, 1998, 34:825-840.

[9] Southward SC, Radcliffe CJ, MacCluer CR. Robust nonlinear stick-slip friction compensation. ASME Journal of Dynamic Systems[J]. Measurement and Control, 1991,113:639-645.

[10] Markicwica B R. Analysis of the computed-torque drive method and computer-controlled manipulator. Technology Memo[M], 33-601, Jet Propulsion Lab, Pasadena, CA,1973.

[11] 杨盐生, 贾欣乐. 不确定系统的鲁棒控制及其应用[M].大连: 大连海事大学出版社, 2003.

[12] Scott L. Delp, Frank C. Anderson, Allison S. Arnold, Peter Loan, Ayman Habib, Chand T. John, Eran Guendelman,and Darryl G. Thelen, OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement[J].IEEE Transactions on Biomedical Engineering,2007,54(11): 1940-1950.