基于帝国主义竞争算法的切削参数优化
陈志楚,李 聪,张超勇
(1. 湖北汽车工业学院 电器信息与工程学院,十堰 442001;2. 华中科技大学 机械工程学院,武汉 430074)
0 引言
数控加工技术是现代自动化、柔性化及数字化生产加工技术的基础与关键技术。切削参数的合理选择与优化,直接关系能否合理地使用刀具与机床,对提高生产率,提高加工精度及表面质量,降低生产成本都有重要作用,是实现整个切削过程优化的关键。随着各种新加工材料的不断涌现,以及数控加工机床、加工中心和柔性制造系统的广泛运用,在传统的CAD/CAM系统中仅依靠个人经验来确定切削参数己远不能适应时代的发展。而运用现代切削理论、数学建模和模型分析方法寻求切削参数的最优组合,则是切削参数优化的一个重要发展方向,是实现高效数控加工技术的关键。
帝国主义竞争算法[15]最初是由Atashpaz-Gargari and Lucas于2007年在对基于人口数量最优化算法的著作中提出。在算法中, 每一个个体都被定义为一个国家,同时,所有的国家被分类为两类,即帝国主义国家和殖民地。帝国主义国家为最初时人口数量最有优势的国家,而剩下的国家即为殖民地。每个国家的力量被用来指明它的健康程度。在该算法的反复使用过程中,帝国之间相互竞争以获得尽可能多的殖民地为目的。更有力量的帝国有更高的可能性去占领更多的殖民地,而力量薄弱的帝国将逐渐失去他们的殖民地。当所有的殖民地都被一个帝国占有时,该算法即为结束。在连续函数优化方面帝国主义竞争算法在效率和质量方面超过遗传算法和粒子群优化算法。因此,本文引入帝国主义竞争算法求解切削参数优化问题。
1 切削参数优化的数学模型
切削速度、进给量和切削深度统称为切削用量三要素。由于切削深度对刀具耐磨度的影响较切削速度和进给量要小,而且可根据工件余量和具体的加工要求来确定,这里视为已知量,不进行优化。因此,模型的设计变量包括切削速度v和进给量f,在铣削加工中,考虑的是每齿进给量fz。对于数控切削加工,因采用无级调速,所以切削参数是连续变量。切削参数优化问题的目标函数选择生产率,表现形式为加工工时。
由于切削加工过程中包含多种实际约束,并且是非线性的。主要有:机床、刀具、夹具等所组成的工艺系统的加工能力;零件加工质量的要求;包括刀具寿命约束在内的经济性约束等。所以,切削参数的数学模型是非线性、多约束的连续函数问题的优化。下面以铣削加工为例建立优化模型。
1.1 目标函数
引入以最大生产率为目标的切削参数数学模型。进行批量生产时,完成一道工序的铣削加工工时为[2~4]:

式中,Tw为完成一道铣削加工的总工时;Tm为工序的切削时间;Th为单工序铣削加工中由于刀具磨损导致的平均一道工序的换刀时间;Tc为工序之间的换刀时间;Tot为除换刀时间以外的其他辅助时间,包括工件的装卸载时间、机床及刀具准备时间等。
工序切削时间Tm的表达式[2~5]:

式中,D为刀具直径;L为切削长度;v为切削速度;fz为铣刀每齿进给量;Z为铣刀齿数。
由于刀具磨损导致的平均一道工序的换刀时间Th的表达式:
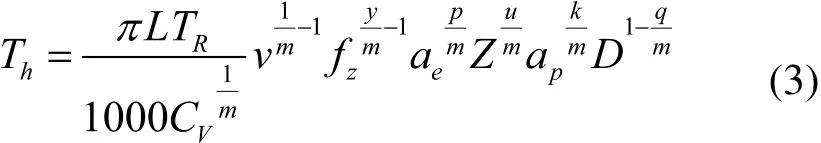
式中,L为切削长度;TR为刀具磨损的换刀时间;v为切削速度;fz为铣刀每齿进给量;ae为铣削宽度;Z为铣刀齿数;ap为铣削深度;D为刀具直径;CV、m、y、p、u、k、q为铣刀的刀具耐用度系数。
综合式(1)~式(3),目标函数为:

1.2 约束条件[2~5]
实际加工中的切削参数必须满足上面提到的各类型约束,具体如下。
1.2.1 切削速度约束
数控机床需满足切削速度约束,表达式如下:
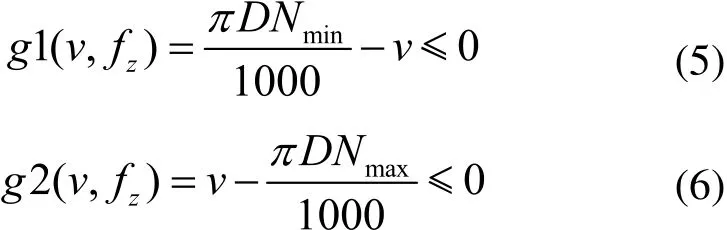
式中,Nmin、Nmax分别为主轴最低和最高转速。
1.2.2 进给量约束
对铣削加工而言,每齿进给量满足的约束条件如下:

式中,vfmin、vfmax分别为机床最小和最大切削进给速度。
1.2.3 机床切削力约束
机床进给方向切削力应小于主轴最大进给力,表达式如下:
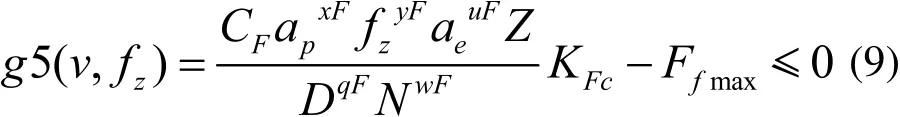
式中,Ffmax表示机床主轴的最大进给力;N为主轴转速,CF、xF、yF、uF、qF、wF、KFc为切削力系数。
1.2.4 切削扭矩约束
切削扭矩不能超过主轴最大扭矩。表达式如下:
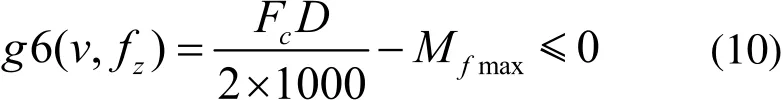
式中,Mfmax为机床主轴的最大扭矩。
1.2.5 机床功率约束
切削功率应小于规定的最大有效切削功率,表达式如下:
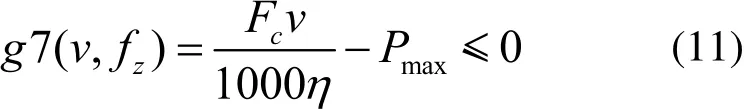
式中,˜为机床功率有效系数;Pmax为机床最大有效切削功率。
1.2.6 粗糙度约束
零件还需满足表面粗糙度要求,表达式如下:

式中,r~为刀具的刀尖圆弧半径;Rmax为表面粗糙度的最大值。
2 基于帝国主义竞争算法的切削参数优化
2.1 帝国主义竞争算法流程
帝国主义算法流程描述如下:
1)初始化帝国主义竞争算法的参数:Npop, Nimp
2)随机生成Npop作为国家的人口数量。选择Nimp最好的国家作为帝国并根据他们的能力规定他们的殖民地数量;
3)如果终止条件未得到满足,则重复下列步骤;
4)内部位置交换;
5)帝国主义竞争;
6)淘汰弱小的帝国;
7)保留最终剩余的帝国,其适应度取值作为最优解。
流程图如图1所示。
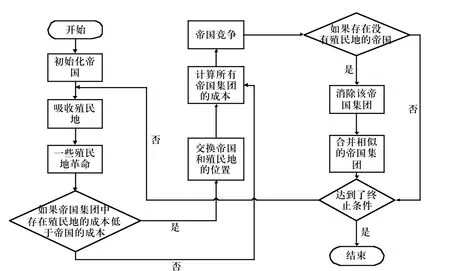
图1 帝国主义竞争算法流程图
2.2 帝国集团的初始化
在一个NVAR维的最优化问题中,一个国家即为一个1×NVAR的矩阵。该矩阵定义如下[16]:

此处,Pi为被优化的变量。这些在国家属性中的变量为浮点数。国家中的每个变量可以被理解为这个国家的社会政治属性。在算法中几时要求我们寻找到最小的成本值。每个国家的成本由变量所组成的函数f决定:
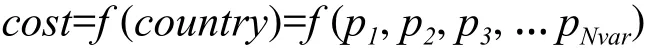
为了开始该最优化算法,必须初始化国家数量Ncountry.我们选择Nimp个最优力量的国家来形成帝国集团。剩下的Ncol个最初国家作为这些帝国集团中的殖民地。

图2 初始化帝国集团:帝国拥有的殖民地越多,它所代表的五角星越大
为了形成最初的帝国集团,殖民地依据各帝国的力量情况决定。即:一个帝国集团最初拥有的殖民地数量应直接与其力量所占比例相关。为了能按比例分配殖民地,每个帝国的成本被定义为:
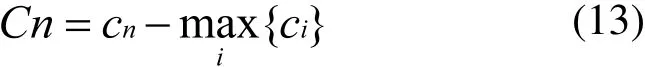
在这里,Cn为第n个帝国的成本。计算了所有帝国的成本后,帝国的相对力量定义为:
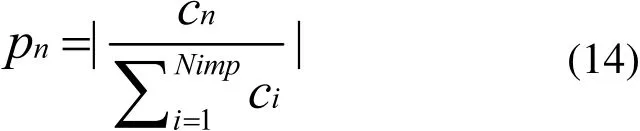
最初的殖民地的分配依赖于其所属的帝国集团的力量。从而最初的殖民地分配为:
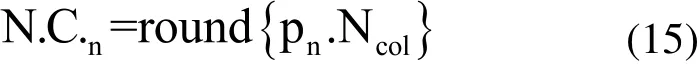
在这里,N.C.n为第n个帝国所拥有的殖民地数量。如图2所示的初始化帝国集团,越大的帝国集团拥有更多的殖民地数量,同时,弱小的集团拥有较少的殖民地。在该图中,帝国1组成最有力量的帝国集团,于是它拥有最多的殖民地数量。
2.3 帝国集团内部调整
为了实现吸收壮大的目的,帝国试图去吸收它们的殖民地并使其成为帝国的一部分。更准确的说,殖民地沿着坐标轴向着帝国移动。移动过程如图3所示。考虑一个二维最优化问题,殖民地在由文化和语言组成的坐标轴中被帝国吸收。殖民地将会不断地向帝国移动,最终将使殖民地完全被帝国吸收。

图3 殖民地向其相关帝国的移动
在图3中,x为一个服从均匀分布的随机数x~U(0, β×d),在这里β为比1大的数,同时˜为殖民地与帝国的距离。b>1将使殖民地从两边都离帝国更近。帝国对殖民地的吸收并不直接导致殖民地向帝国的移动。即是说,殖民地并不一定依照向量所示方向向帝国移动。为了更好模型化这个事实,引入一个随机的角度作为移动的方向。在图中显示了新的方向。在该图中,参数θ服从均匀分布。θ~U(-γ,γ),在这里γ为角度范围。然而˜和˜是随机的。在大多数情况中,我们将˜设置为 2,˜设置为π/4(Rad)。
革命是指在力量和组织结构的基础方面在相对短时间内发生变化。在ICA的术语中,革命使一个国家的社会政治特征突然产生变化。即是说,与帝国的吸收不同,殖民地是随机的在社会政治坐标轴中突然发生位置上的改变。图3和图4是在文化语言坐标轴中的革命过程。这种革命增加了该算法的搜索过程同时组织了国家形成早期的局部收敛。算法中的革命率显示的是每个殖民地随机改变它们位置的比例。一个较高的革命率会降低算法的搜索效果并降低收敛率。在我们的应用中,我们将革命率设定为0.3.即是指帝国集团中有30%的殖民地会随机改变它们的位置。

图4 一个国家社会政治特征的突然改变
2.4 交换帝国和殖民地的位置
当殖民地向帝国移动的过程中,殖民地可能会到达一个成本比帝国要低的点。在这种情况下,帝国和殖民地即交换它们的位置。而后,算法将由在新位置的帝国吸收新位置的殖民地过程继续下去。如图5所示为帝国和殖民地交换位置的过程。在改图中,最好的殖民地由深色表示,该殖民地比其帝国的成本要小。如图6所示为殖民地和帝国交换位置后的状态。

图5 交换殖民地和帝国的位置

图6 交换位置后的帝国和殖民地的状态
在殖民地和帝国向着目标最小值移动的过程中,一些帝国可能会移动到相似的位置,如果两帝国之间的位置要小于初始位置,它们将会合并为一个新的帝国集团。原帝国集团的殖民地将会成为新帝国集团的殖民地,同时新帝国的位置将由原帝国中二者之一的位置所决定。图7和图8显示的合并过程。

图7 合并前的帝国集团

图8 两帝国合并后的状态
2.5 帝国集团竞争
一个帝国集团的总力量主要由它的帝国力量所决定。可是殖民地的力量也对帝国集团的力量有影响。一个帝国集团的总成本由式(16)所决定[16]:
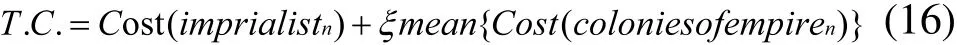
此处,T.C.为第n个帝国集团的总成本。ξ为一个较小的正数。ξ越大会使殖民地对帝国集团的影响越大。在大部分的情况下ξ取0.1被认为是最好的。
每个帝国集团都试图占领并控制其他帝国集团的殖民地。帝国竞争过程中,强国将更强,弱国将更弱。帝国竞争一般先选出最弱帝国集团,并使其他帝国集团竞争去占领该集团。图9显示帝国竞争。在这个过程中,基于各自的力量,每个集团都有占领最弱集团的可能性。从另一个方面来说,最弱国不一定确定被最强国家占领,但是越强的集团占领弱集团的可能性越大。为了开始这个竞争过程,首先最弱的帝国集团的一个殖民地将被选出来,并确定每个国家占领的可能性。占领可能性Pp依据帝国集团的总力量所决定:

图9 帝国竞争:帝国越有力量,越有可能占领最弱帝国集团的殖民地
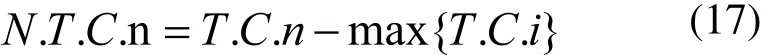
此处,T.C.n和N.C.n为第n个帝国集团的总成本和相对成本。依据相对成本,每个帝国的占领可能性由下式决定:
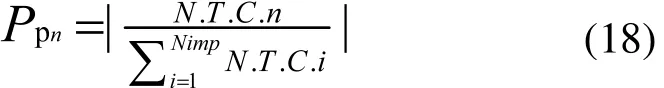
为了将在帝国集团中将上述的殖民地分类,我们引入如下向量P:

向量R是与向量P具有相同规格的向量,其元素服从均匀分布:

向量D由向量P减去向量R所得:

向量D中元素值最大的对应帝国集团即会占领上述的殖民地。
这样选择帝国集团的过程与遗传算法中选择母类的轮盘赌过程相似。但是这里的选择方法比相关的轮盘赌过程要快。因为这个过程并不需要计算累积分布函数,并且选择过程仅仅基于可能性的值。因此,帝国集团的选择过程可以完全替换遗传算法中的轮盘赌,并增加执行速度。上述步骤将会持续下去直至实现国家收敛并且达到成本最小的目标。不同标准可用来结束该算法。一种思想是设定最大迭代次数。或者当仅剩一个帝国集团时即结束该算法。
2.6 约束处理
依前所述,切削加工过程中存在各类非线性约束条件。ICA算法也是针对无约束优化问题的随机寻优算法,因此,必须结合约束处理技术,才可用于解决切削参数优化问题。目前流行的约束处理技术主要是罚函数法[17]。文献中考虑了粒子的历史约束状态,本文结合二者进行约束处理。针对本文数学模型,罚函数如公式(22)所示:

式中,α为罚因子。根据公式(22)来评价帝国和殖民地,如果当前帝国没有违反约束条件,则以目标函数为评价标准,否则,根据罚函数来评价帝国。
3 实例分析与结果比较
3.1 模型与算法中的参数设置
3.1.1 切削参数优化模型中相关参数设置
前面引入参考文献[2~4]中的模型,这样便于比较结果,同理,也采用相同的实例。
刀具直径:100mm;切削长度:159mm;切削深度:2mm;切削宽度:60mm。
铣刀齿数:4;
刀具刀尖直径:1mm;
表面粗糙度最大值:3.2 ;
刀具磨损导致的换刀时间:600s;
主轴最低转速:45转/分 ;
主轴最高转速:6000转/分;
最小进给速度:3mm/s;
最大进给速度:8000mm/s ;
机床主轴最大进给力:8000N;
机床主轴最大扭矩:200N×m;
机床主轴最大有效功率:7.5Kw;
机床功率有效系数:0.8;
查切削用量手册[5]得刀具耐用度系数:
Cv:1067 m:0.2 y:0.2 p:0.15 u:0.1 k:0.1 q:0.25;
切削力系数:
Cf:7900 xf:1.0 yf:0.75 uf:1.1 qf:1.3 wf:0.2 kfc:0.25。
3.1.2 ICA算法中的参数设置
ICA算法中,初始国家数量为20,其中帝国数量为5,殖民地数量为15;ξ为0.1,β设置为2,γ 设置为 π/4(Rad);罚因子 α=1。
3.2 结果比较与分析
将ICA算法随机测试20次,所得最好结果、平均值、最差结果和标准差结果与文献[4]进行比较,如表1所示,其中PSO+LS代表采用局部搜索的PSO混合算法;PSO代表基本的PSO算法;SA代表模拟退火算法;Dynamic与Adaptive分别代表采用动态及自适应惩罚策略的遗传算法。从表中可以看出,ICA算法最好解、平均解和标准差的值均优于其他算法,表明了ICA算法应用于切削参数优化问题的有效性和优越性。

表1 不同算法随机测试20次的统计结果
4 结论
本文在考虑机床加工和工件的实际约束的基础上,建立以最大生产率为目标函数的铣削参数数学模型,然后应用帝国主义竞争算法对数控机床的铣削参数进行寻优,并进行了实例验证。同时,在理论研究的基础上,开发出相应的原型系统软件,本文的研究内容和成果可为帝国主义竞争算法求解其他相似类型问题提供启发和借鉴。
[1] 邹云. 铣削加工切削参数只能选择系统的研究与开发.2004.
[2] 凌玲, 黄豪, 胡于进等. 基于遗传算法的多种切削方式集成参数优化[J]. 机械制造. 2009 (2): 43-47.
[3] 高亮, 高海兵, 周驰. 基于粒子群优化的切削参数优化算法研究[A]. 第五届全球智能控制与自动化大会会议论文集(4)[C]. 2004: 2867-2871.
[4] 高海兵. 粒子群优化算法及其若干工程应用研究[D]. 华中科技大学出版社. 2004.
[5] 艾兴, 肖诗纲. 切削用量简明手册. 第三版[M]. 北京: 机械工业出版社. 2004.
[6] Kennedy J, Eberhart R.C. Particle swarm optimization[C].Proc of IEEE Intl Conf on Neutral Networks, Perth,Australia, 1995: 1942-1948.
[7] 王凌, 刘波. 微粒群优化与调度算法[M]. 北京: 清华大学出社. 2008.
[8] K.E. Parsopoulos, M.N. Vrahatis. Particle Swarm Optimization Method for Constrained Optimization Problems[J]. Intelligent Technologies-Theory and Applications: New Trends in Intelligent Technologies, 2002, 214-220.
[9] Y. Shi et al., Cellular particle swarm optimization. Inform Sci. (2010), doi:10.1016/j.ins: 2010.05.025.
[10] 吕凯. 元胞自动机的研究及模型的建立[D]. 哈尔滨理工大学. 2007.
[11] 夏小翔, 曾建潮, 高慧敏. 基于元胞自动机的小生境微粒群算法[J]. 计算机工程与应用. 2007(11): 66-68.
[12] M. Tolouei-rad, I.M. Bidhend. On the optimization of machining parameters for milling operations. Intl. J. of Machine Tools & Manufacture. 1997, 37(1): 1-16 .
[13] C.Carlos. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms:a survey of the state of the art. Computer methods in applied mechanics and engineering. 2002. 191(11): 1245-1287 .
[14] Wassila Bouzid. Cutting parameter optimization to minimize production time in high speed turning. Journal of Materials Processing Technology. 161 (2005) 388–395.
[15] Esmaeil Atashpaz-Gargari,Caro Lucas.Imperialist Competitive Algorithm: An Algorithm for Optimization Inspired by Imperialistic Competition 1-4244-1340-0/07_c 2007 IEEE.
[16] Ebrahim Hosseini Nasab, Mohsen Khezri, Morteza Sahab Khodamoradi, Esmaeil Atashpaz Gargari, European Journal of Scientific Research,ISSN 1450-216X Vol.43 No. 4 (2010): 495-506.
[17] 何郁波, 马昌凤, 田亚娟, 非线性互补问题的罚函数法,1001-7437(2005)06-61-03.
[18] P. Padilla, B. Anselmetti, L. Mathieu, M. Raboyeau,Productionm’ ecanique Dunod, 1986.
[19] J. Paulo Davim, A note on the determination of optimal cutting conditionsfor surface finish obtained in turning using design of experiments, JMPT 116 (2001) 305–308.
[20] J. Paulo Davim, Design of optimization of cutting parameters for turning metal matrix composites based on the orthogonal arrays, JMPT 132(2003) 340–344.

