基于似然的航迹关联算法研究*
刘国栋 吴媛媛
(1.91550部队 大连 116023)(2.海军北海舰队司令部 青岛 266071)
1 引言
现有的用于航迹关联的算法通常可以分为两类:一类是基于统计的方法,另一类是基于模糊数学的方法[6~7],本文提出了几种基于似然的航迹关联算法,它通过建立似然函数[9~11]来反映代表同一目标的不同传感器间的航迹相似度,通过对似然函数的评估来决定一个最佳全局关联假设,从而达到航迹关联的目的。
2 问题的描述
我们对来自Ns个传感器的航迹建立一个数学形式的描述,设每个传感器上报的航迹数为Ti,i=1,…Ns,那么第i个传感器的航迹表示为Zj,i,j=1,…Ti,对应的状态估计为zj,i,协方差为Rj,i,定义一个集合量元组T,假设每个元组由来自同一个目标的状态估计组成,这样所有元组的组合就构成了一个全局的关联假设H,一个元组对于一个传感器最多只能包含它的一条航迹,且元组必须是非空的,所以每个元组的大小一定是限制在0<NT≤Ns之间。
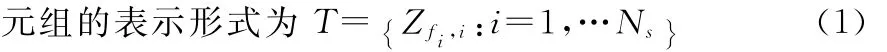
fi是来自传感器i的航迹,如果一个元组中没有航迹来自传感器i,那么fi=0,传感器上报的每一条航迹都是一个元组的成员,且一条航迹只能在一个元组中,因此,在一个全局假设H中,所有元组的大小之和一定等于所有传感器上报的航迹数之和,即
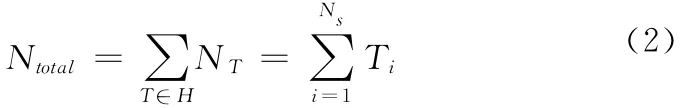
由于量测和过程噪声的独立,所以和不同目标关联的航迹之间是独立的,因此全局假设H的似然p(z1,1,…,可以分解为多个元组的似然,式(1)中定义的元组的似然可以表述为
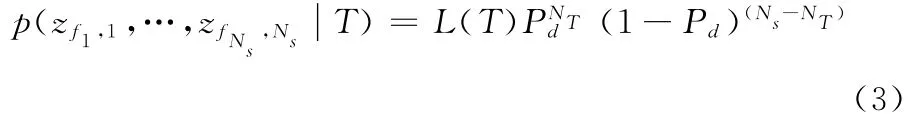
这里L(T)为元组联合概率密度函数,Pd代表传感器的探测概率,且
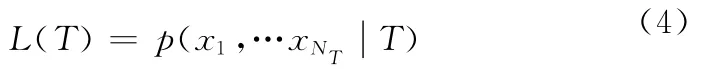
式(4)中的航迹观测xi和协方差Ri,i=1,…NT与航迹的状态估计和误差协方差是一一对应的,设所有的全局假设H构成的集合为W,则利用所有元组似然的乘积可以形成最大似然(ML)方法
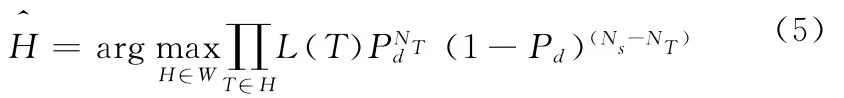
假设没有虚警、漏警的理想情况(Pd=1),这样每个传感器上报的航迹数就等于目标的总数,即N0=T1=…=,ML方法可以简化为

当来自不同传感器的航迹源于同一目标时,ML方法是最优的,但是组成元组的航迹所对应的目标真实状态往往是未知的,所以一个似然的精确表达式是难以获得的,这就需要一些合适的似然近似来替代,本文将对四种元组似然的近似进行描述和分析,通过利用关联误差来达到对似然近似的目的。
为描述方便,下文将元组的大小NT统一表述为N,这样一个元组中和不同航迹关联的传感器可记为i=1,…N。对于第i个传感器来说,xi是 M维目标状态的估计,Rii是估计误差协方差,一个元组中的N条航迹,状态估计记为
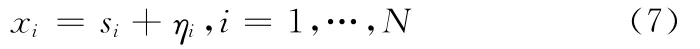
这里si是来自第i个传感器的真实目标状态,ηi是状态估计误差,该误差服从均值为0方差为Rii的高斯分布,由于共同的过程噪声,来自不同传感器同一目标的航迹之间存在互关联,不妨设第i个传感器和第k个传感器对同一目标的互协方差为E{ηiη′k}=Rik。在一个元组中认为N条航迹源于同一个目标,即有s1=s2=…=sN=s,所以式(7)可以简化为
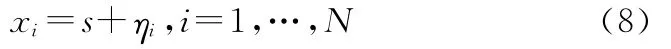
设XN是元组中N条航迹的串联,即
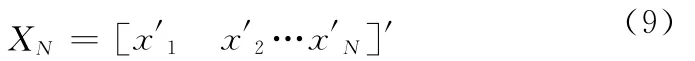
对应的误差协方差矩阵为

令NM×M维矩阵IN=[IMIM…IM]′(11)
这里IM为M×M的单位阵。
对元组中的航迹进行融合,从而得到融合航迹
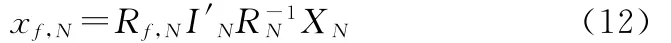
这里Rf,N是融合航迹的协方差
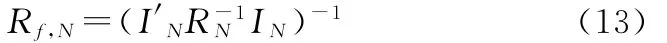
通常情况下,认为航迹间误差是相互独立的,即Rik=0,i≠k,这样式(12)、(13)可以简化为

3 近似似然航迹关联
3.1 顺序似然
为讨论问题的方便,认为航迹间的互协方差为零。
元组顺序似然的表达式为

对于一个元组来说,当元组似然达到最大时,认为元组中对应的航迹源于同一个目标,利用该准则可以对不同传感器的航迹进行有效的关联,下述几种似然均是采用此关联准则。
图1给出了顺序似然的流程图。
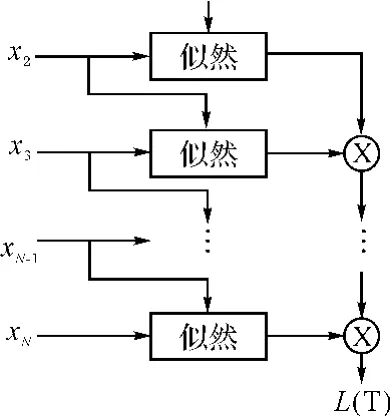
图1 顺序似然流程图
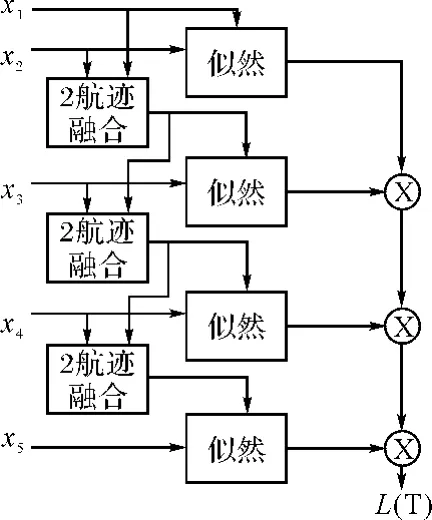
图2 分布先验似然的顺序形式(N=5)
图中每个似然的输入xi代表传感器的航迹,顺序似然可以通过一系列的最优2维分配来实现,首先,对来自传感器1和2的航迹通过2维算法进行关联,保持关联结果固定,然后对来自传感器2和3的航迹进行关联,保持关联结果固定,这样重复,一直到来自传感器N-1和N的航迹进行关联,最后由各个2维关联结果的乘积得到N维关联结果,即顺序似然。各个2维关联之间可以独立进行,然而该方法不是最优的,因为它依赖于各传感器航迹序列的顺序。
3.2 全局似然
全局似然的表达式为
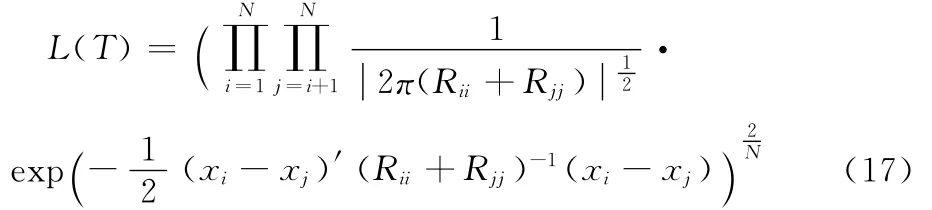
式(17)中的指数2/N是对全局似然维度的归一化,使之与顺序似然的维度相一致,全局似然不依赖于航迹序列的顺序,但它和顺序似然一样,都认为航迹误差是相互独立的。
4 仿真分析
为了讨论问题的方便,这里均考虑三个局部节点的情况,且认为误差互协方差均为零。
仿真环境1:三部雷达测距和测角误差均为σρ=170m,σθ=1°,用蒙特卡洛方法进行50次仿真,每次仿真14步,采样间隔T=4s,假设在两传感器的公共观测区域内有60批目标,模拟目标在一个二维平面上具有变速、存在有意和无意机动,具有可以认为在速度上变化的过程噪声,目标初始速度在4m/s~1200m/s之间均匀分布,初始航向在0~2π之间均匀分布,目标初始位置在x=190km,y=135km处按正态分布产生,三局部节点的位置分别为(125km,125km)(235km,130km)、(190km,160km)。
在模拟目标运动时,取
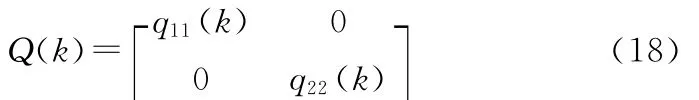
仿真结果1:
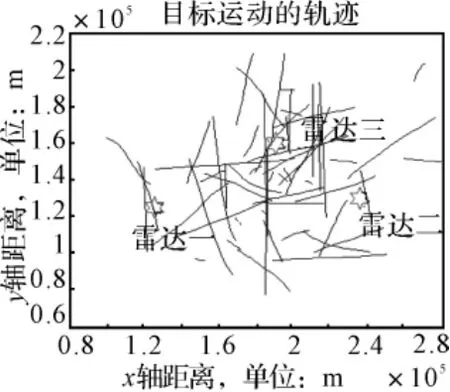
图3 60批密集目标的运动轨迹
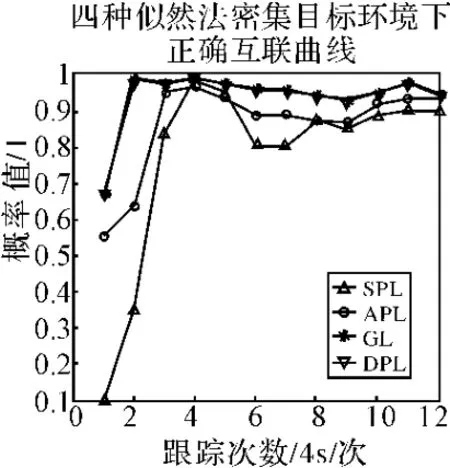
图4 四种似然法正确关联率对比
仿真分析1:图3给出了在公共观测区域60批密集目标的运动轨迹及三个局部节点的位置。图4给出的是对图3所示的公共区域目标的航迹分别采用两种基于似然的航迹关联方法仿真50次后的平均正确关联率曲线,由图4可以看出在密集目标环境下广义似然和分布先验似然有较好的正确关联效果,并且这两种方法的关联效果几乎一致,全局似然的正确关联效果次之,但也能维持较高的正确关联率,顺序似然的正确关联效果最差,全局似然正确关联率高于顺序似然的原因在于它合并了所有的两两航迹间的联合,而顺序似然只是合并了顺序两两航迹间的联合。由仿真结果可以看出这两种基于似然的航迹关联算法均能达到较好的关联效果,只是顺序似然在关联初始阶段稍差。
仿真环境2:三部雷达测距和测角误差均为σρ=100m,σθ=0.6°用蒙特卡洛方法进行50次仿真,每次仿真14步,采样间隔T=4s,假设在两传感器的公共观测区域内有N=10批目标,模拟目标在一个二维平面上做匀速直线运动,具有可以认为在速度上变化的过程噪声,目标速度为vx=600m/s,vy=600m/s,目标初始位置在x=-8km,y=-15km附近产生,目标之间的间距设为d=200m,三局部节点 的 位 置 分 别 为 (125km,125km)(235km,130km)、(190km,160km)。
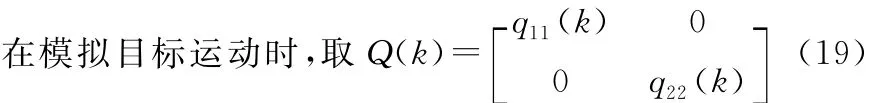
仿真结果2:
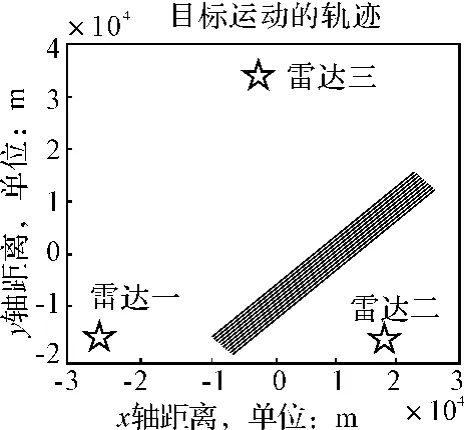
图5 10批平行目标的运动轨迹
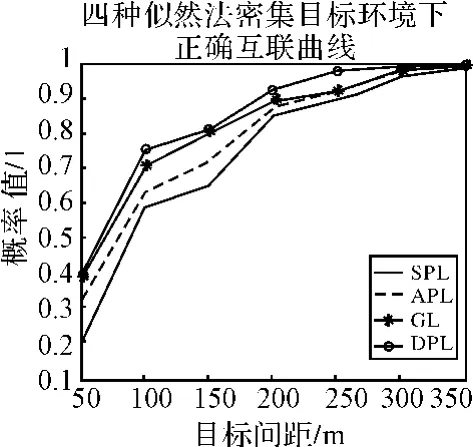
图6 两种似然法正确关联率随目标间距变化比较图
仿真分析2:图5给出了在公共观测区域10批平行目标的运动轨迹及三个局部节点的位置。图5给出的是对图6所示的公共区域目标的航迹分别采用四种基于似然的航迹关联方法仿真50次后的平均正确关联率随目标间距变化曲线,由图6可以看出在平行目标环境下,两种似然关联算法正确关联率均是随着目标间距的增大而增大,其中在相同目标间距的情况下,分布先验似然的关联效果最优,广义似然、全局似然和顺序似然的关联效果依次次之,并且均能达到较好的关联效果。
5 结语
本文先对似然关联进行了简单的问题描述,接着给出了两种基于似然的航迹关联算法,这两种算法通过建立似然函数来反应航迹间的相似程度,从而达到航迹关联的目的,最后通过两种典型仿真环境下的仿真结果可以看出,基于似然的航迹关联算法对密集目标和平行目标均能达到较好的航迹关联效果。
[1]Chen,H.,Kirubarajan,T.,and Bar-Shalom,Y.Performance limits of track-to-track fusion versus centralized estimation:Theory and application.IEEE Transactions on Aerospace and Electronic Systems,39,2(Apr.2003):386-400.
[2]Chong,C.-Y.,Mori,S.,Barker,W.H.,and Chang,K.-C.Architectures and algorithms for track association and fusion.IEEE Aerospace and Electronic Systems Magazine,15,1(Jan.2000):5-13.
[3]Rao,B.S.,and Durrant-Whyte,H.F.Fully decentralized algorithm for multisensor Kalman filtering.IEEE Proceedings,Pt.D,138,5(1991):413-420.
[4]Bar-Shalom.Y., William.D.B., Multitarget-Multisensor Tracking,Applications and Advances[M].Artech House,2001:155-157.
[5]Bar-Shalom.Y.A Tutorial on Multitarget-Multisensor Tracking and Fusion.1997,IEEE National Radar Conference,15 May 1997,Syracuse,NY.
[6]何友.分布式多传感信息融合算法研究[D].清华大学,2006.
[7]何友,王国宏,陆大金,等.多传感器信息融合及应用[M].(第二版).北京:电子工业出版社,2000:203-206.
[8]李启元,段立,李亚楠.海战场目标航迹间距离聚类方法[J].计算机与数字工程,2010(5).
[9]Blackman,S.S.,and Popoli,R.Design and Analysis of Modern Tracking Systems.Boston:Artech House,1999:7-14.
[10]Bar-Shalom.Y.,and Chen,H.Multisensor track-to-track association for tracking with dependent errors.ISIF Journal of Advances in Information Fusion,1(July 2006),3-14.
[11]Pattipati,K.R.,Kirubarajan,T.,and Popp,R.L.Survey of assignment techniques for multitarget tracking.In Y.Bar-Shalom and W.D.Blair(Eds.), Multitarget-Multisensor Tracking:Applications and Advances,vol.3.Norwood,MA:Artech House,2000:77-159.

