基于协同学的超视距协同空战模型研究*
陈 正 于 乐
(1.海军航空工程学院研究生管理大队 烟台 264001)(2.91980部队 烟台 264001)
1 引言
协同学是以系统论、信息论、控制论、突变论等为基础,采用统计学和动力学相结合的办法,通过类比分析,建立一整套数学模型和处理方法来研究由完全不同性质的大量子系统(如电子、原子、细胞、神经元、力学元、光子、器官、动物乃至人类)所构成的各种系统,研究这些子系统是如何通过合作在宏观尺度上产生空间、时间或功能结构以及从无序到有序的演变规律[1]。其思想表明:一切开放系统,无论是宇观系统还是宏观系统,或是微观系统,无论是自然系统,还是社会系统,都可以在一定的条件下呈现出非平衡的有序结构,都可应用协同学[2]。许多研究人员利用协同学理论在经济、交通、教育、军事等领域进行了相关应用[3~6]。
在现代高技术条件特别是信息化条件下的航母编队防空作战中,舰载机编队遂行远程防空任务与敌方空中力量交战时不再只是航空武器装备之间的对抗,而是空中力量体系与体系之间的对抗。当我们把遂行超视距协同空战任务的基于预警机指挥引导的舰载战斗机编队作为一个独立的复杂动态系统进行分析时,其目标是取得远程防空作战(空战)的胜利;其元素是参与空战的每一架舰载战斗机以及预警机;其子系统是每个战术编队。同时我们也应该认识到,组成作战飞机的各种航电、动力、武器、火控、飞控等系统又可以看成是上一级协同空战子系统(飞机)的子系统。因此,整个协同空战系统就形成一个庞大的金字塔,构成了协同空战的多层复合的总系统。其中各子系统既有纵向指挥隶属关系,又有横向协同关系。它们之间存在着物质、能量、信息等方面的关系和交流。
因此,协同学理论同样可以作为探索舰载战斗机超视距协同空战复杂系统结构和秩序的有效手段,应用协同学的基本原理,寻找影响空战系统变化的控制因素,进而研究如何发挥空战系统内子系统间的协同作用。
本文把协同学理论引入到超视距协同空战中,构建超视距协同空战的协同模型,实现舰载战斗机编队协同作战整体效用的最大化。
2 协同学理论
1)系统与子系统。系统是这样的一种集合,它存在目标、元素和关系,具体来说它的元素或元素组合为着一个或一组共同目标而做出贡献、发生关系。也叫这样的系统为简单系统。系统各元素都存在变域,所有变域的乘积空间叫做系统空间。一个系统中元素的子集合构成了所谓的“子系统”[2]。在舰载战斗机超视距协同空战中,子系统是每个战术编队,单架战机是系统的元素。
2)序参量。序参量是由子系统的协作而产生,是大量子系统集体运动的宏观整体模式有序程度的参量,序参量是描述系统宏观有序度或宏观模式的参量。当控制参量达到一定的“阙值”时,子系统关联和子系统独立运动之间的平衡被打破,关联胜过独立运动,开始起主导作用,从而使系统中出现了由关联所决定的子系统之间的协同运动,于是宏观上呈现出有序结构。序参量表示系统的有序结构和类型,是子系统介入协同运动程度的集中体现[7]。
3)支配原理。支配原理体现了相变时系统内子系统协同作用的特点,即由慢弛豫参量支配快弛豫参量形成协同作用。支配原理是经过归纳总结提出的系统相变时遵从的基本原理,是协同学理论框架中的最主要支柱。
4)自组织。在一定的环境条件下,由系统内部自身组织起来,并通过各种形式的信息反馈来控制和强化这种组织的结构称为自组织结构,相应的描述和分析方法称为自组织理论。它是协同学的核心理论。
5)协同。协同是系统中诸多子系统的相互协调、合作或同步的联合作用,集体行为。一个复杂的系统,若子系统互相配合产生协同作用和合作效应,系统便处于自组织状态,系统在宏观上和整体上表现为具有一定的结构或功能。不同的系统性质会有不同,但都从不同侧面揭示了从宏观到微观、从机械运动到生物运动的和谐性和协调性。
协同系统是指由许多子系统组成的、能以自组织方式形成宏观的空间、时间或功能有序结构的开放系统。系统演化过程中从无到有的变化通过序参量来表示。序参量来源于子系统之间的协同,能够指示新结构的形成,同时起着支配子系统行为的作用。协同学认为,一个系统从无序到有序转换的关键在于由一个大量子系统构成的开放系统内部发生的协同作用。它强调系统内部的关联及系统发生变化时要素间的互相配合与耦合。
可从协同成员对协同的贡献、对各自观点的表达方式上将协同方式分为以下三种[6]:(1)协商(或对策)方式。(2)合作的方式。这种方式的协同工作可以描述成一个协作群体共同解决一个(或多个)问题,或协作完成一项(或多项)共同的任务。(3)创造的方式。
3 舰载战斗机超视距协同空战中的协同研究
协同空战系统由一组具有自治性、主动性、反应性等特征的舰载战斗机组成,由于单架舰载战斗机能力和资源受限,舰载战斗机需要相互协同合作来完成空战任务,因此要构建一个有效的协同空战系统,需要详细分析和设计系统内的协同过程,通过舰载战斗机协同合作去研究解决一些复杂的优化问题。
预警机和舰载战斗机存在能力、控制上的异构;舰载战斗机的数量、战术、机动规划及指挥关系可能是动态的;目标、环境的不确定性;舰载战斗机飞行员的“心理”状态不可预测。以上特征增加了空战系统协同合作的复杂性。
假设有遂行超视距协同空战任务的系统X,有n个元素为x=(x1,x2…,xn)∈X表示各舰载战斗机,令所考察的系统功能为W,则有W=Φ(x1,x2…,xn)
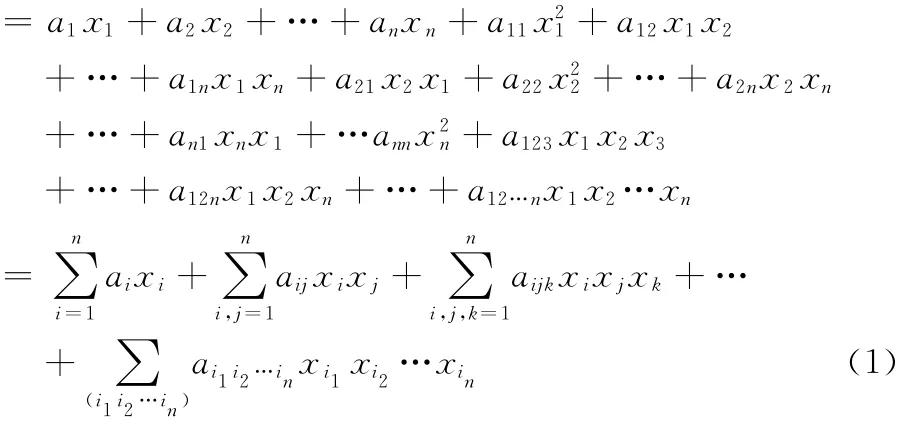
式(1)取的是n个元素的各种“排列式”,而一般协同空战系统只需取作“组合式”即可,即有:
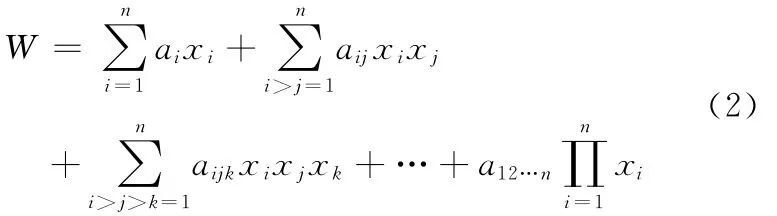
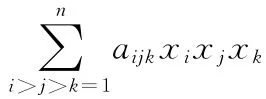
目前提出的解决空战系统中协同问题的关键方法有如下三种:
1)组织协同。采取组织的、分层组织的结构,提供一个具有系统视野的预警机,由它来解决各个舰载战斗机的冲突,确保系统行为一致。预警机通过自身的探测设备或从舰载战斗机组收集信息、创建计划、向舰载战斗机分配任务来确保全局一致。预警机始终是系统中起决定作用的序参量。
2)为了协同的合约。合同网协议(CNET)是最著名的协同合约。采取市场机制,通过任务共享实现有效合作,并引入不遵守承诺的惩罚措施,利用金融选择定价理论获得在不确定性环境中的灵活协同方案。
3)为了协同的规划。将协同问题抽象成规划问题,目前存在集中式和分布式两种舰载战斗机规划模型。规划需要节点共享和处理大量的信息,所以涉及到更多的计算和通信。
上述方法有一定的适用性但都存在局限。而协同学理论认为,在混沌的运动阶段,系统中有数个序参量交互起作用,以此推动着结构形成的过程。在结构形成过程中,不是在始终地增加无序,而是把后来无序的各个部分吸引到已存在的有序状态中来,最终促成结构的协同。本文认为舰载战斗机超视距协同空战协作完成复杂任务的过程与此类似,可以应用该理论研究舰载战斗机超视距协同空战中的协同过程。
4 基于协同理论的舰载战斗机超视距协同空战协同模型
协同学中,用n个状态变量描述系统,如q=(q1,q2,…,qn),对于不同的系统,qi表示不同的参量。存在单一变量的系统和多变量的复杂系统,都可以用微分方程或方程组来描述,用积分表示的方程的解来描述系统的演化过程。本文先引入自组织理论中对多变量复杂系统的描述,进而推导出舰载战斗机超视距协同空战合作的协同模型。
4.1 多变量复杂系统的协同学描述
现实中大量存在的是多变量的复杂系统。考虑用下标u来标志多变量系统中的子系统,每个子系统由一组变量(qu1,qu2,…,qun)所描述;同时,引入一组对系统产生作用的外力(F1,F2,…,Fm)。在变量q之间存在耦合,耦合常数也可以与外力Fj有关。这种情况下,该系统的协同学方程为[8~10]:
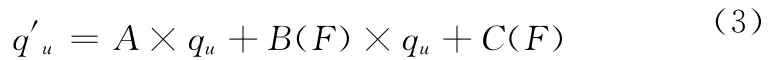
对于C也满足同样的假设。要求矩阵A的特征值实部全部为负,即Re{λ}<0,A的行列式,A有逆矩阵。按照对B和C所作的假设,只要F充分小,总有行列式。虽然式(3)是qu的线性方程,但求其一般解仍是非常困难的。利用协同学的绝热近似(绝热消去法)可以得到它的唯一解。为此,假设F远比系统qu随时间的变化慢,令q′u=0。此时,式(1)便化为简单的代数方程,其解为
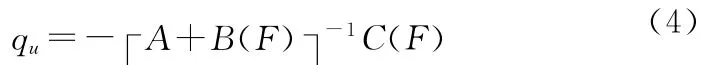
对不同的子系统有不同的A、B和C,即在式(4)中进行如下的替换:

则解为qu=- [Au+Bu(F)]-1Cu(F),此式表明了状态变量qu对“力”F的响应。
4.2 空战系统协同模型
超视距协同空战系统中,由于空战目标威胁所产生的系统“外力”可以转化为系统元素协同所产生的“力”并引入第4.1节的方法进行量化,并以此为基础构建舰载战斗机超视距协同空战的协同模型。首先以一组变量描述各个舰载战斗机,则空战系统可以描述为q(q1,q2,…,qn)。其中qi代表某个舰载战斗机的能力与目标参量,则空战系统的演化方程为
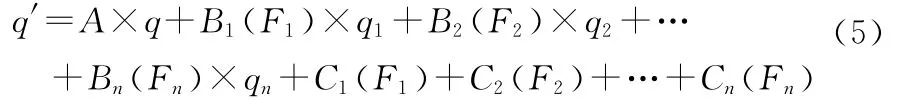
其中,F表示因为空战目标威胁使舰载战斗机的协同所产生的“力”;矩阵A表示空战系统对系统演变的阻尼效应,即当多个舰载战斗机按照自己选择的目标各自为战时,系统自己演变的效应;矩阵B1,B2,…,Bn表示舰载战斗机子系统协同机制的“力”对子系统舰载战斗机序参量q1,q2,…,qn之间耦合的影响;矩阵C1,C2,…,Cn表示舰载战斗机超视距协同空战协同对单个舰载战斗机目标实现的影响。
为讨论方便,令
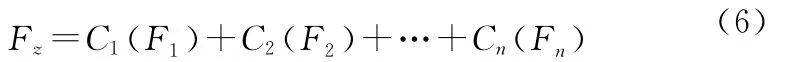
将式(5)代入(6)得
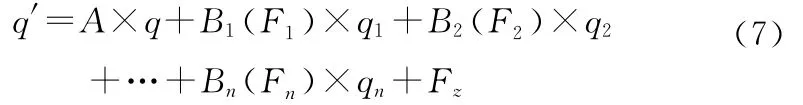
同样地,令q′=0,并遵从与上面相同的假设条件,可以得到式(7)的唯一确定解:
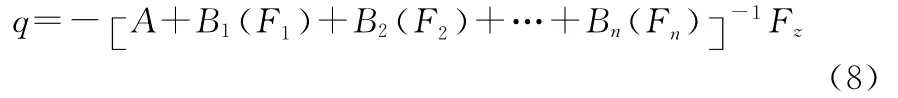
式(8)代表了多个舰载战斗机协同对系统任务完成的作用。
上述模型适应了舰载战斗机超视距协同空战合作的复杂性和任务阶段性,为舰载战斗机超视距协同空战协作研究引入了协同理论,以此来评价不同的舰载战斗机协作机制的协同效果,更好地解决了超视距空战协作中的单架战机能力独立性和空战目标一致性问题。
5 模型分析
基于协同学的舰载战斗机超视距协同空战协同模型量化了协同效应,在模型中:Fi表示舰载战斗机为协同活动的付出;矩阵A表示系统自身对系统演变的阻尼效应,即当系统无协同机制下,舰载战斗机在各自目标的驱动下,系统空战可以达到的协同效应;矩阵B1,B2,…,Bn表示协同机制对各舰载战斗机努力的影响,即在特定协同机制下舰载战斗机的行为模式;C1,C2,…,Cn表示特定的协同机制下,单个舰载战斗机目标实现程度的量化。
在空战系统协同过程中,随着外界环境的变化以及系统任务的进展,在不同的阶段,系统需要不同的协调方法来指导各舰载战斗机之间的协调合作。这些特点符合自组织系统演变的开放性和远离平衡态的条件。按照自组织的理论在系统由无序到有序、再由有序演变到更高的有序状态,需要新的序参量来引起系统的演化。所以本文认为在舰载战斗机超视距协同空战完成一个复杂任务中,协同任务的完成需要不断适应外界和自身的变化,从而确立舰载战斗机的任务目标,优化协同效应,调整努力程度和行为模式。
因此在空战过程中,为使协同效应q最大化,优化矩阵A及矩阵B1,B2,…,Bn元素的取值,然后根据矩阵的取值来指导各个舰载战斗机的行为模式,以此达到舰载战斗机超视距协同空战协同的优势互补。如果有多种协同方法可以采用,那么可以通过对协同机制参数转换为式(8)中的矩阵参数来评价各个方法的协同效应,选择最优的协同方法,在时间、空间等资源的约束下达到空战协同效应的最优化。该模型适用于完成复杂实时任务的空战系统,它是随环境变化自适应调整行为的动态模型。
6 结语
在舰载战斗机超视距协同空战合作研究中引入协同学理论,将空战系统中各舰载战斗机的能力、目标量化为影响协同结果的变量,将协同方法量化为序参量。给出了基于协同学的舰载战斗机超视距协同空战的协同合作模型。该模型是随环境变化自适应调整行为的动态模型,可以评价不同协同方法对舰载战斗机任务完成的协调程度,为最优协同方法的选择提供了依据。本文首次将协同学理论引入到空战系统合作中,为空战系统合作问题的解决提供了新的理论依据。下步的工作应将协同的效果模型进一步研究,得出超视距协同空战系统的协同度模型并结合超视距协同空战进行分析。
[1]郭治安.协同学[M].北京:科学出版社,1989:2-3.
[2]高隆昌.系统学原理[M].北京:科学出版社,2005:1-2.
[3]李义,赵新国.作战指挥系统的协同学特性及演化问题研究[J].装备指挥技术学院学报,2010,21(2):14-18.
[4]杨兆升,陈昕,王海洋,等.协同学理论应用于ITS研究[J].辽宁工业大学学报,2008(1):48-51.
[5]孙珠峰,赵亮,薛昌友.基于协同学理论的舰艇CGF反潜态势识别研究[J].系统仿真学报,2006,18(9):2616-2619.
[6]胡旦华,马永光,张宇晴.Multi-Agent系统中合作策略的研究[J].计算机仿真,2004,21(3):130-132.
[7]郭治安.协同学入门[M].成都:四川人民出版社,1988:23-25.
[8]卜先锦.指控单元战术协同效果分析、建模与应用[D].国防科学技术大学,2006(1):15-16.
[9]卜先锦.军事组织协同的建模与分析[M].北京:国防工业出版社,2009:30-31.
[10]孙玲.协同学理论方法及应用研究[D].哈尔滨工程大学,2009(5):18-20.

