自适应NURBS插补中陷波滤波器的设计*
张颖颖
(三门峡职业技术学院,河南 三门峡 472000)
高速高精度的运动控制是机械制造业自动控制领域的核心技术,而插补模块是实现这一技术的重要模块,其中自适应NURBS曲线插补技术是工程应用中的典型代表。运动速度、控制精度以及整个系统的动力学特性是自适应NURBS曲线插补技术涉及到的几个重要因素,其中动力学特性在现代高速、高精度、复杂运动轨迹的数控加工系统中尤为重要。
动力学特性对加工过程的影响主要体现在加工运动轨迹出现尖角时、受进给速率变化影响较大的拐角点、高频分量以及与执行机构固有频率相同的频率分量等这几个方面。数控机床运动控制器要追踪加工轨迹的尖角处非常困难,同时尖角处进给的加速度很容易超出机床所能承受的范围。在插补的过程中往往会遇到这样运动加速度超过机器本身所能承受范围的情况,这会产生过度波动而导致加工精度降低,产品质量得不到保证。针对这个问题,传统的解决方法是在数控机床控制器最后的执行阶段给出一定的加速度,避免超限,该处理效果并不十分理想[1]。
为了能够在计算加工轨迹的同时将动力学影响考虑在内,可以运用数字滤波的方式,对执行插补指令后的数据进行滤波处理,滤除能够引起机床共振的频率分量,保障运动控制的高精度。采用陷波滤波器可以在完成DSP插补控制的前提下,插补数据经由串行口直接导入PC机,对其进行陷波滤波处理,滤除与机床执行机构固有频率同频的分量,避免出现共振,实现动力学滤波,提高控制精度。
1 滤波器的设计方法
1.1 数字滤波器
数字滤波器是对输入的数字信号按照一定的要求进行数值运算等处理,实现保留有用信号,滤除无用信号等功能的算法或装置。最常用的两种数字滤波器为FIR和IIR,分别被称为有限响应冲击数字滤波器和无限响应冲击数字滤波器[2]。二者相较各有所长,FIR线性相位,需要较高的阶数,相比之下,若要达到同样的性能指标,IIR所需要的阶数远小于FIR,所需要的存储单元少,经济而且高效。由于NURBS线性插补后是以序列形式的坐标做为输出,因此本滤波器采用IIR模型。
1.2 设计方法
设计IIR数字滤波器一种方法是先设计一个相应的模拟滤波器,然后根据要求转换成满足实际需要的数字滤波器,由于模拟滤波器有许多可用的公式和参数表格,设计过程相对比较简单。另一种方法是借助计算机进行辅助设计,在确定最佳准则的前提下,求出数字滤波器的系统参数,此种方法灵活,可根据不同的需求快速的调整滤波器的系统参数。本滤波器采用MATLAB软件仿真获得滤波器的系统参数来设计IIR滤波器。
MATLAB具有强大的矩阵运算、数值分析及信号处理功能,其信号处理工具箱综合了各种滤波器的设计、仿真和分析技术,为设计数字滤波器提供了方便快捷的设计工具。将低通模拟滤波器变换到具有相同性能的数字滤波器的经典设计方法,即将模拟滤波器的系统传递函数映射为数字滤波器的系统传递函数,是MATLAB信号处理工具箱提供的IIR数字滤波器设计方法之一。要实现从H(s)到H(z)即s域与z域之间的转换,可以通过脉冲响应不变法或双线性映射法来实现[3]。
脉冲响应不变法可以利用信号工具箱中的函数impinvai和以下公式实现求解过程:
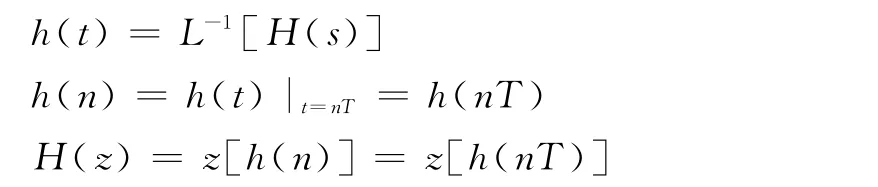
双线性变换法则是通过S=2fs(z-1)(z+1)和信号处理工具箱中的bilinear函数实现将传递函数从H(s)到H(z)的变换[4]。
MATLAB提供的第二种设计方法是直接利用IIR数字滤波器完全设计函数,根据具体需要产生自由阶数常用的带通、带阻、高、低通等任何形式的滤波器。
2 陷波滤波器的设计与实现
带阻滤波器的阻止带宽窄到一定范围内时,就被称为陷波滤波器。陷波滤波器的设计和实现是通过利用MATLAB信号处理工具箱提供的设计工具,以具有代表性的四种不同几何特征的曲线作为目标测试曲线,用滤波器对其进行处理后,对处理结果进行误差分析。以统计学为依据,主要从两个方面作出评价,一是速度的稳定性,二是位置控制的精确度。
2.1 确定中心频率
实际应用系统执行机构的固有频率是选定滤波器中心频率的重要依据,只有满足这个条件才能达到滤除产生执行机构共振频率分量的目的。以实测电机作为执行机构,测试其固有频率,用以选定本陷波滤波器的中心频率,测试数据如图1所示。

图1 实测电机实验
由测试结果可知电机的固有频率处在低频频段。不同的曲线所含有的频率分量也不同,曲线越复杂,其频率分量越丰富,而滤波器的带宽也会对滤波处理后的结果产生影响,从而使得误差发生变化。针对不同的曲线,将采用不同的中心频率,以及不同的频带宽度。因此,选定滤波器的中心频率为50Hz、100Hz两段。
2.2 基于DSP实现陷波滤波器
可编程DSP芯片具有诸多优点,用它来实现陷波滤波器不仅稳定而且精确度高,可以通过编程修改滤波器的系统参数,调整滤波器的功能,灵活方便。滤波器实现所需要的硬件设备包括DSP和ARM9运动控制板、PC机,其中DSP和PC机的数据采集由相应的软件控制,将插补后的数据导入PC。
本陷波滤波器采用IIR模型中最常用的II型滤波结构,滤波器的系统参数、通过运用双线性变换法求得,如表1所示。
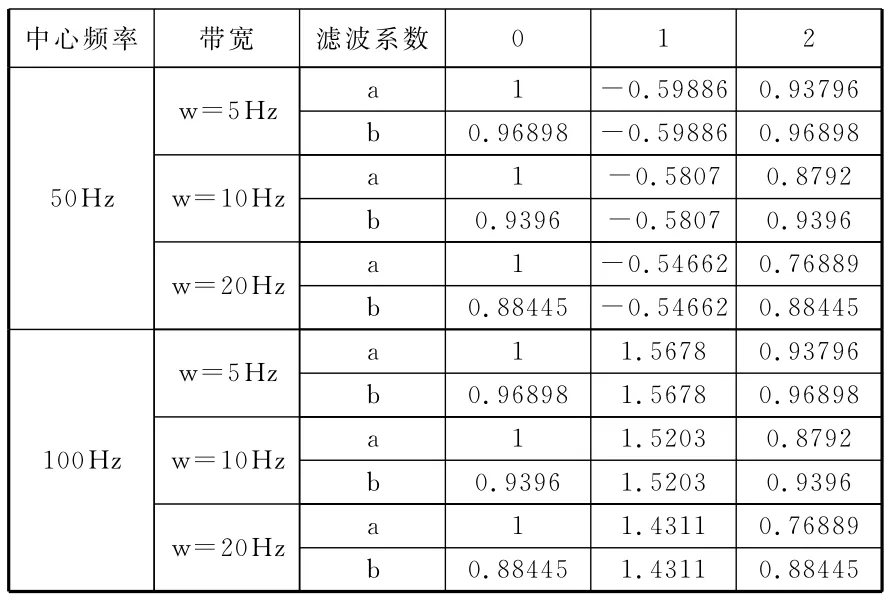
表1 陷波滤波器系数
当陷波滤波器选取带宽5Hz,中心频率为50Hz时,滤波器的传递函数H(z)应为:
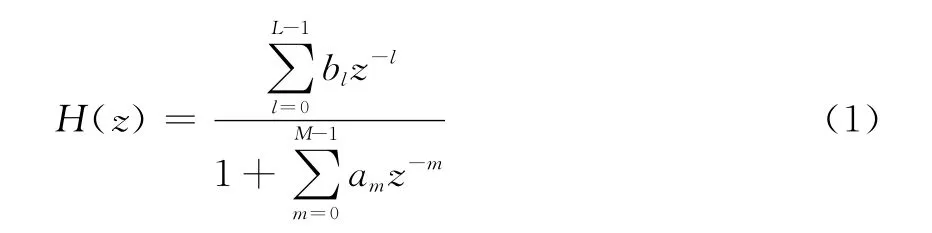
代入滤波器的系数a、b,则H(z)应表示为:
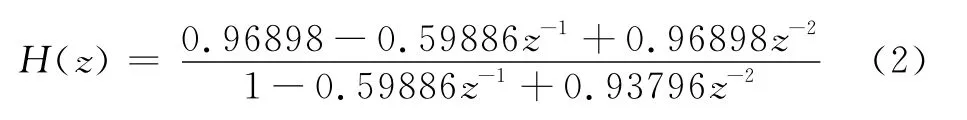
由此可获得:

3 滤波器性能分析
根据相对误差ex(i)、ey(i),位置偏差e(i)以及RMS、Max和Mean这三个指标对滤波器的性能进行分析和评价。
3.1 目标测试曲线
选用直线、圆、星形曲线和桥形奇点曲线这四种代表性的离散型值点曲线作为目标测试曲线,由于其具有不同的几何特征,因此在滤波后呈现不同的特点。其中,直线和圆的几何特征较简单,星形曲线作为一种封闭曲线的代表,具有几何对称的特点,桥形奇点曲线则属于非封闭、不对称、曲率复杂的曲线代表。如图2所示,“◇”表示NURBS插补定点,点之间的曲线为插补后的离散型值点的连线。

图2 目标测试曲线
对这四种曲线进行陷波滤波处理,针对每一种曲线陷波滤波后的性能进行分析。不同特征的曲线选用不同中心频率的滤波器,曲线越复杂,包含的频率分量越多。对于直线和圆形曲线,滤波器的中心频率选择50Hz,而对于星形曲线和桥形奇点曲线则选用中心频率为100Hz的滤波器。
3.2 滤波结果及性能评价
3.2.1 目标曲线-直线

表2 直线轨迹滤波误差评价
直线的几何及频率特性简单,从直线滤波后的误差评价表中可以得出,滤波器的带宽越小,误差评价的各项指标也越小。滤波后误差评价数据如表2所示,以带宽为10HZ下的各项指标为例,其中ex(i)和ey(i)的Mean指标分别为0.03616%和0.03619%,由于插补周期一定,故可将ex(i)和ey(i)看作是x轴和y轴速度的相对误差,评价数据表明,滤波前后直线的速度比较稳定;Max指标分别为9.54685%和9.54648%,与Mean值相差近9%,意味着在滤波处理后的某个区域相对误差较大。位置误差e(i)的Mean指标为0.002147mm,Max指标为0.002890mm,表明位置误差均值大约为2μm,而最大误差不超过3μm,能够满足高精度位置控制的要求。
3.2.2 目标曲线-圆
圆轨迹包含了很多频率分量,其瞬时角频率不断变化。平面圆轨迹可以分解x、y为两部分,x方向为正弦轨迹,y方向为余弦轨迹。滤波后误差评价数据如表3所示,ex(i)和ey(i)的Mean指标比直线轨迹的Mean指标数值大,但均控制在1%以内,随着带宽的减小,其值随之减小。ex(i)和ey(i)的滤波处理后的误差最大值分别为25.24689%和30.13169%,该指标也随带宽的减小而减小。带宽为20Hz时e(i)的Mean值达到8μm,这一指标已经能够满足工业上的一般精度要求,若对带宽加以调整,可将其控制在4μm以下,因此,对于圆形轨迹,滤波器带宽不宜过大。

表3 圆轨迹滤波误差评价
3.2.3 目标曲线-星形曲线
星形曲线是一类呈几何对称、曲率均匀变化的封闭曲线。对其进行滤波处理,速度稳定性较好,滤波后误差评价数据如表4所示,在ex(i)和ey(i)的误差均值被控制在0.05%之内;带宽为5Hz时,误差均值为0.00057036mm,即精度能够达到0.5μm,精度非常高。

表4 星形曲线轨迹滤波误差评价
3.2.4 目标曲线-桥形奇点曲线
桥形奇点曲线是一类曲率均匀变化且对称不封闭的曲线,对其进行滤波处理,能够获得较好的速度稳定性及较高的精度,滤波后误差评价数据如表5所示,e(i)的Mean指标较小,均控制在1μm以内。
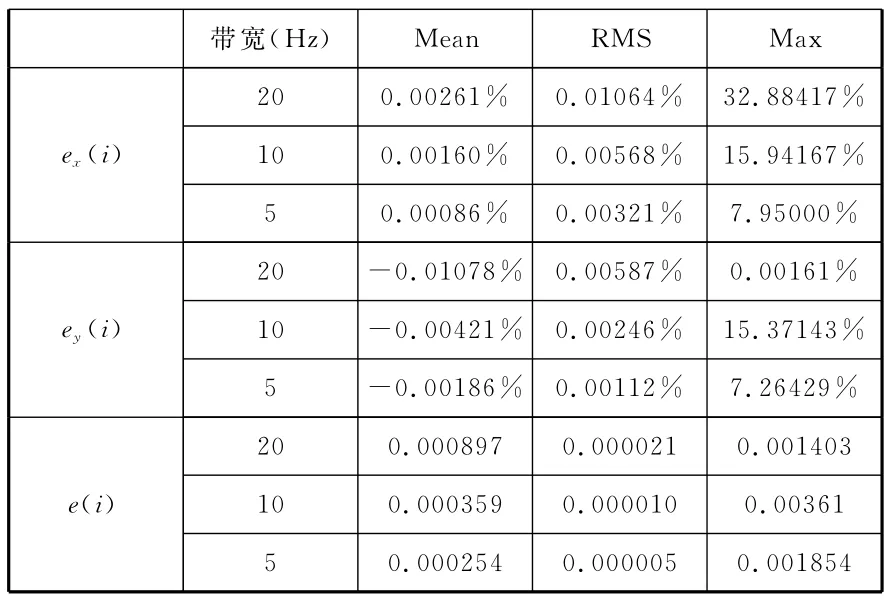
表5 桥形奇点曲线轨迹滤波误差评价
4 总结
由实验结果可以得出,直线滤波产生的误差很小;星形曲线和桥形奇点曲线位置偏差也都在1μm以内;而圆形曲线通过选取合适的滤波器带宽也能够将偏差控制在4μm。对于四种曲线轨迹进行陷波滤波处理,均能达到较高的精度,并获得较好的速度稳定性。NURBS插补技术中运用动力学陷波滤波器能够解决执行机构的共振问题,提高运动控制的精度。
[1]姬晓天,施寅.NURBS的概念与使用[J].计算机辅助设计与制造,1998,(12):25-26.
[2]廖永进.基于DSP的NURBS曲线插补控制[J].DSP开发与应用,2006,(6):181-183.
[3]罗军辉,罗永江.MATLAB7.0在数字信号处理中的应用[M].北京:机械工业出版社,2005:63-115.
[4]张明照,刘政波,刘斌.应用MATLAB实现信号分析和处理[M].北京:科学出版社,2006:183-245.
[5]C.C.Lo.Feedback command generators for CNC machine tools[J].Journal of Manufacturing Science and Engineering-Transactions of the ASME,1997,119(4):587-592.
[6]M.Weck,G.Ye.Sharp corner tracking using the KF control strategy[J].Annals of CIRP,1990,39(1):437-441.

