独立时差计算公式的错误分析＊

刘慎熊 周 黎 张长清

（武汉交通职业学院，湖北 武汉 430065）

1 问题的提出

在现行各版本施工组织学教材中，求单代号网络计划的独立时差的计算公式皆为：

可是，在教学和实践的过程中，发现在某些工程中应用这个公式计算单代号网络计划的独立时差时，其结果与同一工程的双代号网络计划是不同的。不是数值不对，就是出现了不可思义的负数。（这个不可思义，是指这个负数的绝对值甚至大于前后工作的总时差之和）。我们知道一个工程既可以表达为单代号网络计划，也可以表达为双代号网络计划。而且，同一项工作的所有时间参数在这两种计划中应该是一致的。但在使用公式（1）时独立时差却出现有时不一样的问题，这是什么原因呢？

双代号网络计划独立时差的计算公式是：

公式（2）定义的双代号网络计划的独立时差的概念及推导是清楚的、正确的，因此公式（2）是不会有问题的。而对公式（1）的max｛IFh｝，总感觉含义似是而非，且无法作出概念上的清析解释，这样看来，问题或许就出在公式（1）上。为了找到答案，必须对公式（1）作深入的研究和探讨。

2 独立时差的含义及公式分析

独立时差是指在既不影响紧前工作的最迟完成，又不影响紧后工作的最早开始的前题下，本工作的机动时间。考虑到自由时差对紧后工作没有影响，独立时差也可以表达为是自由时差中对紧前工作最迟完成不产生影响的那一部分机动时间。也就是说，独立时差是在本工作的自由时差中减掉其对紧前工作最迟完成产生影响的那部分后，所得的差。公式（1）和公式（2）似乎都有点这个意思。

在双代号网络计划图中，本工作的紧前工作中既有实工作也有虚工作，它们的最迟完成时间是一样的，都是LFh－i，因此本工作自由时差对所有紧前工作的最迟完成产生的影响都是一样的，即都等于LFh－i－ESi－j＝IFh－i，从自由时差中减去这个影响值，剩下的差就是本工作的独立时差，可见公式（2）是正确的。

但是在单代号网络计划图中，由于没有中间虚工作，所以在把一项工程的双代号网络图转换成单代号网络图时，就可能会出现某一工作跨越虚工作直接成为本工作的紧前工作。（为了方便，我们把它称为名义紧前工作）。如图1所示：（a）是某双代号网络图的一部分，（b）是該图转换成单代号网络图后与（a）相应的部分。

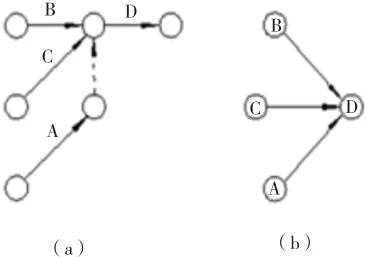
图 1

A工作就是D工作的名义紧前工作，它的最迟必须完成时间值，必然小于或等于其余两紧前工作B和C的最迟完成时间值。那么D工作的自由时差对A工作最迟完成的影响必然小于或等于对B、C两工作最迟完成的影响。故我们要取这个影响的最大值，完全可以不考虑对A工作最迟完成的影响。但是公式（1）却把这个最大值定义为紧前工作相关时差的最大值：max｛IFh｝。这里就没有排除A工作的意思，因为不能保证A工作的相关时差一定比B和C两个工作的相关时差小，相反A工作的相关时差有时确实是最大值。（在后面实例图3上，可以看到这种情况。如：D工作的名义紧前工作A的相关时差是4，而工作B的相关差是0）。也就是说公式（1）考虑了不该考虑的选项，而应该考虑的选项又没有考虑，或者说选择最大值的标准不对。就像是本要选一个统军将才，结果选了一位百发百中的神枪手。这里正确选项应该是“本工作自由时差对所有紧前工作最迟完成产生影响的最大值”，而不是公式（1）中定义的“所有紧前工作相关时差的最大值”，这也许就是问题的根源所在。下面我们用一个实例来应证公式（1）是不正确的。

3 实例论证

图2是某工程双代号网络计划图，经过计算，各时间参数都按标注图例填入相应的位置。而图3是这同一个工程的单代号网络计划图，各时间参数也填入相应的位置。其中单代号网络计划图的独立时差是使用公式（1）计算出来的。

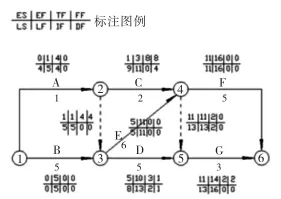
图 2

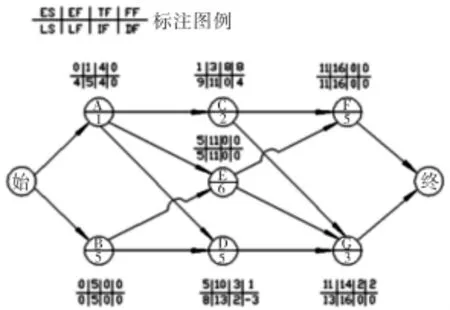
图 3

这两种网络计划中的同一工作各参数应该是完全一致，但是可以发现图3中D工作的独立时差与图2中D工作的独立时差不同。下面是使用公式（2）、公式（1）及定义式计算的过程和结果。

图2是双代号网络计划，独立时差用公式（2）计算：

或者用定义式：

图3是单代号网络计划，独立时差用公式（1）计算，图2中的工作3－5在图3中就是工作D。它有两个紧前工作A和B。用公式（1）DFi＝FFi－max｛IFh｝来计算，则有：

而从图3中可以看到FFD＝1，IFA＝4，IFB＝0。于是有DFD＝1－max｛4，0｝＝1－4＝－3

在这三个答案中，用公式（2）计算的结果是毋庸置疑的，因为，它与使用独立时差的定义式所得到的结果完全一致，那只能说明使用公式（1）所得到的结果是错误的。

4 正确公式的推导

4．1 公式推导

单代号网络计划中独立时差应该根据独立时差的定义及单代号网络图的特点进行推导。

根据独立时差的定义，又考虑到在单代号网络图中因没有中间虚工作，i工作的所有紧后工作的最早开始时间不尽相同，故要取最小值；同样i工作的所有紧前工作的最迟完成时间也不尽相同，故要取最大值。即：

（4）代入（3）得：

又∵TFi＝LSi－ESi

（6）代入（5）得：

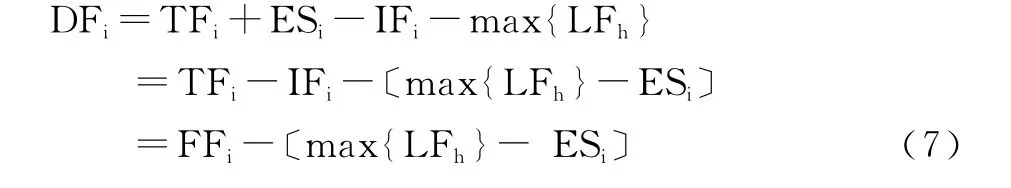
这个（7）式就是我们给出的正确公式。这个公式中max｛LFh｝表示本工作所有紧前工作的最迟完成时间的最大值，这也可认为是排出了那些名义紧前工作。而方括号里面的内容所表达的正是我们前面所说的选项：“本工作自由时差对所有紧前工作最迟完成产生影响的最大值”。这与我们前面分析的结论是吻合的。

4．2 验证

现在我们对图3中D工作的独立时差用（7）式进行计算：

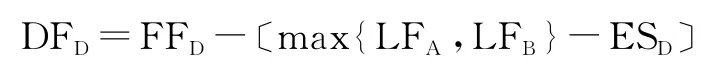
从图2，3中我们知道FFD＝1，LFA＝5，LFB＝5，ESD＝5

即：DFD＝1－〔max｛5，5｝－5〕＝1

可见经过检验，这个式子的正确性是显而易见的。把它用于上面的计算，得出的结果与双代号网络计划的结果是一致的。

5 结论

（1）在计算单代号网络计划独立时差时，应该用（7）式来计算。即：

（2）独立时差出现负数时的含义及计算时应注意的问题。负数表明本工作对紧前工作的最迟完成或者对紧后工作的最早开始产生了影响，或者对紧前紧后工作都产生了影响。这个负数的绝对值就是这个影响程度，但是这个绝对值，不能大于前后工作的总时差之和。因为如果这个绝对值大于前后工作的总时差之和，就意味着本工作的最早开始时间在紧前工作的最早完成时间之前，同时本工作的最迟结束时间在紧后工作最迟开始时间之后。而这是绝对不可能发生的现象，除非算错了，正如本例一样。所以我们认为，如果独立时差算出负数，可以直接填入，没有必要令其等于零。

（3）关于“名义紧前工作”的处理方法，在特殊情况下，即若所有紧前工作都是名义紧前工作时，不能全部排除，必须在这些“名义紧前工作”中取最迟完成时间的最大值。即便是这样，也并不影响公式（7）的正确性。