基于时间序列分析方法在车队健康管理中的应用研究

王 培，张晓玉，柳 丹

（1，2.河南交通职业技术学院，郑州450005；3.湖南巴士公共交通有限公司，长沙410114）

健康管理（Health Management－HM）可提高整体设备的生产效率、可靠性和盈利能力，并确保生产安全[1].这里的健康有多种理解，如系统执行设计功能的能力[2，3]、系统相对预期正常状态的降级或偏差程度[4]等.实质上，健康就是系统的状态，这种状态包括完成相应功能的能力情况、与预期状态的偏差程度等.健康管理则是与健康直接相关的管理活动，通常包括监测、诊断与评估、预测和决策优化与评估四个部分.

1 时间序列

由一连串随机变量z1，z2，z3，…，zn构成的序列称为随机序列，如果该随机序列是按时间顺序排列的，就称该序列为时间序列.假设，我们在时间ti（i＝1，2，3，…，n，…）观测得到zt（t＝1，2，3，…，n，…），即：

此时，就得到了一个时间序列Zt＝｛zt，t＝1，2，3，…，n，…｝，如果同时观测m个相同对象，那么就得到一组时间序列Ztj＝｛ztj，t＝1，2，3，…n，…，j＝1，2，3，…，m｝[5].

时间序列的影响因素分为四类：长期趋势、季节变动、循环变动和不规则变动.

对以上四部分可以通过简单数学关系式得到时间序列的分解模型，分解模型很多，最基本的模型有加法模型和乘法模型，加法模型可以表达为：

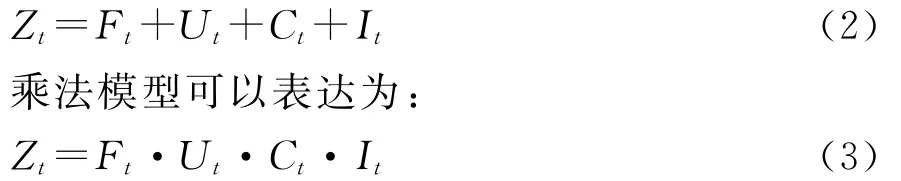
在应用中，将依次确定以上各项，直至剔除确定项后的序列为不规则变动为止．检验是否为不规则变动的最简单方法就是看序列是否为白噪声［6］．下面就本文应用到的建模过程介绍如下．

（1）确定长期趋势Ft：本文采用多项式趋势模型，模型描述如下：

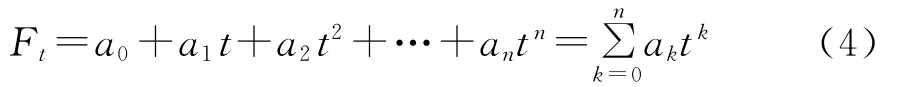
（2）确定季节变动Ut：当确定长期趋势后，在时间序列中减去长期趋势后的部分记为yt＝Zt－Ft．对于季节变动的分析可以采用谐波分析法［7］、隐周期分析［8］等，本文采用谐波分析．

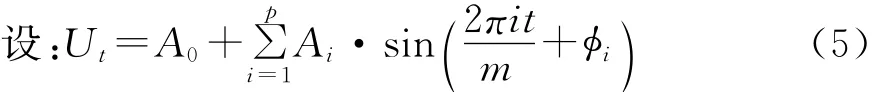
其中m为季节变动的基本周期称为基波，其余各波的周期分别为基波周期为潜波．若时间单位为周，则m＝52，如果为月，则m＝12．

Ai、φi和P分别为振幅、相位和yt中含基波与潜波数目．当P＞1时，意味着yt中含有p－1个潜波．假设yt的季节变动基本周期m＝52，yt时间序列含有n个基本周期，不同基本周期内的yt观测值另记为：

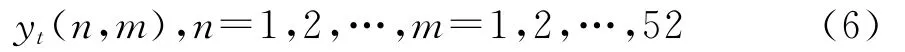
2 实际应用

2.1 数据及预处理

我们收集了某巴士公司一个由22辆车组成的车队近175周（2006年9月1日至2010年1月9日）的失效数据.在本文中，我们将整个车队看成为一个整体，运用分解分析方法对该车队的平均失效次数进行分析.表1给出了该车队部分时间序列数据Nt进行示意.

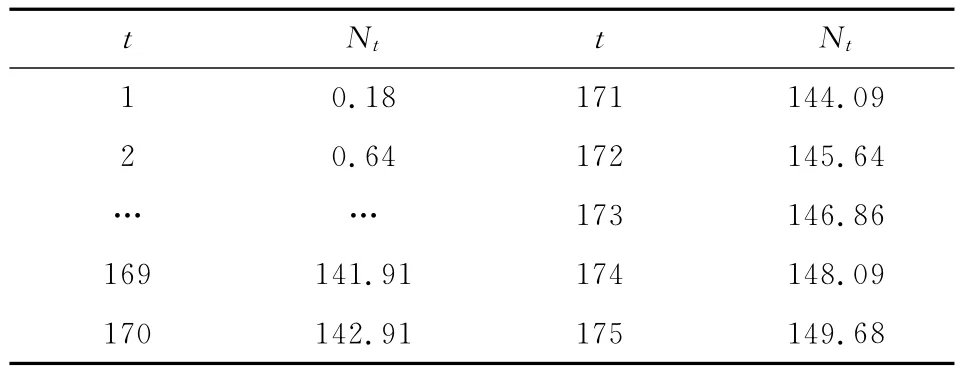
表1 车队平均失效次数的时间序列数据

为了验证模型预测的准确性，本文利用前170周数据建立结构时间序列模型，预测未来171至175周失效次数，并与实际失效次数进行比较.

2.2 建模

根据前述方法，我们有：

（1）长期趋势F170，应用多项式趋势模型逼近解得：

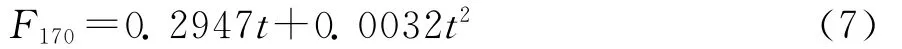
拟合的效果图如图1所示.剔除长期变动后的序列均值不为零，非白噪声序列.接下来进行季节变动的确定.

图1 长期趋势拟合效果

（2）季节变动U170：该车队2007至2009年在1－53周的失效次数统计如表2所示，并以其均值作

表2 2007至2009年在1－53周的失效次数

为真值确定季节变动.我们从图2中的真值曲线可以明显看出，失效次数随着季节变化存在着规律性变动.令式（5）中p＝1，2，…，由最小二乘法进行参数估计，估计的参数及最小误差平方和见表3，当p＝2时其最小误差平方和小于1，故取p值为2.p＝2，3时的季节项拟合效果见图2.

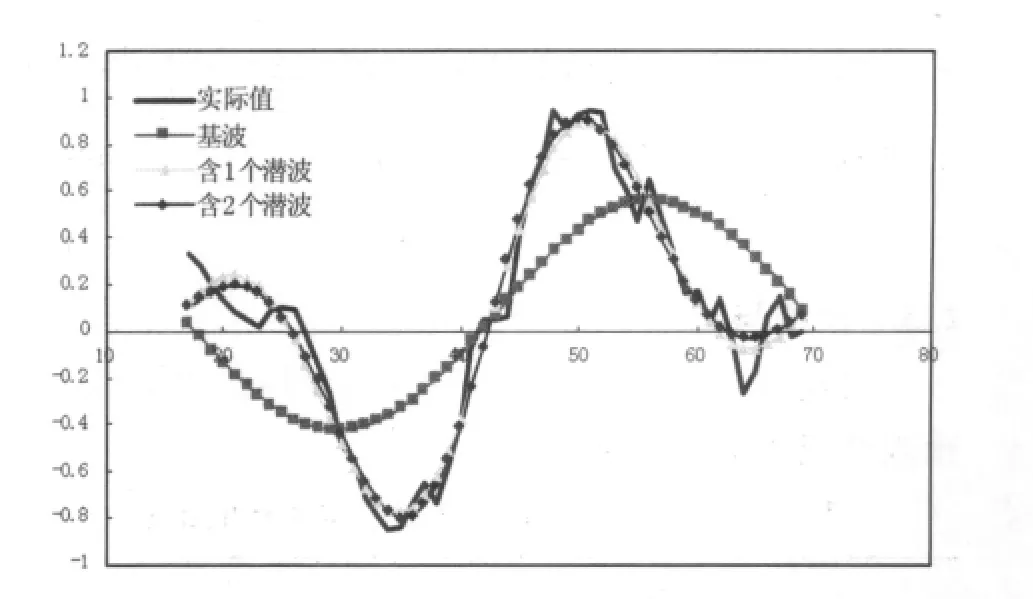
图2 季节项拟合效果

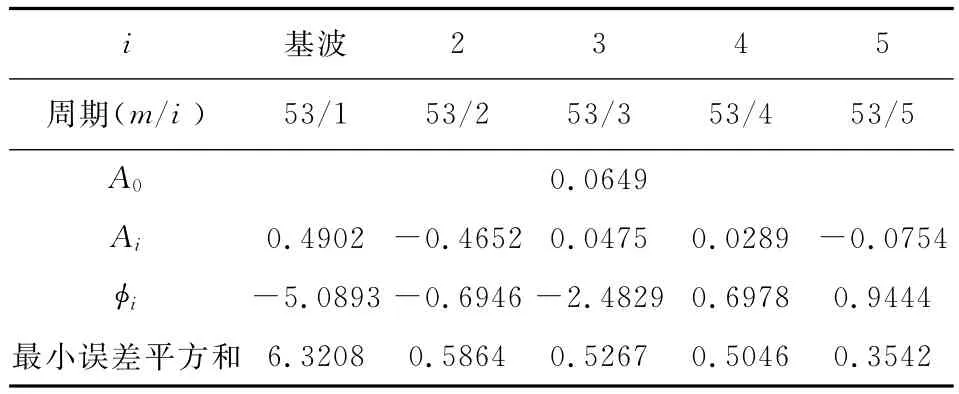
表3 P＝2，3时的参数及最小误差平方和

由此，我们得到季节变动为：

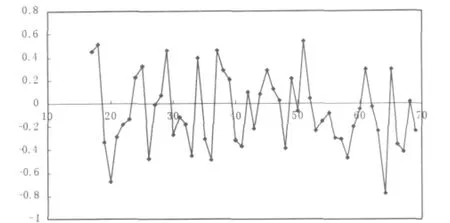
图3 剔除长期趋势和季节变动后的时间序列数据散点图

剔除季节变动和长期趋势后的时间序列数据，如图3所示；且其均值为0.0021，为白噪声.我们认为车队失效数据只存在长期趋势和季节变动.对于长期趋势，我们不难理解为车辆随着使用时间的增长，出现劣化所致.对于季节变动，存在一个潜波和一个潜波.我们可以近似得到式（8）的周期为19.5周，而该巴士公司对车辆进行二级保养的时间间隔平均是17.9周，也就是说季节变动反映的是车辆二级保养效果.至此，我们就确定了t＝170时的模型：

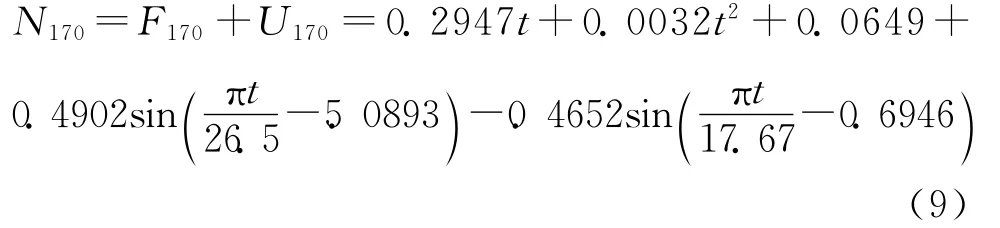
2.3 预测与比较

根据式（9）预测了第171－175周的失效次数，预测结果如表5所示.

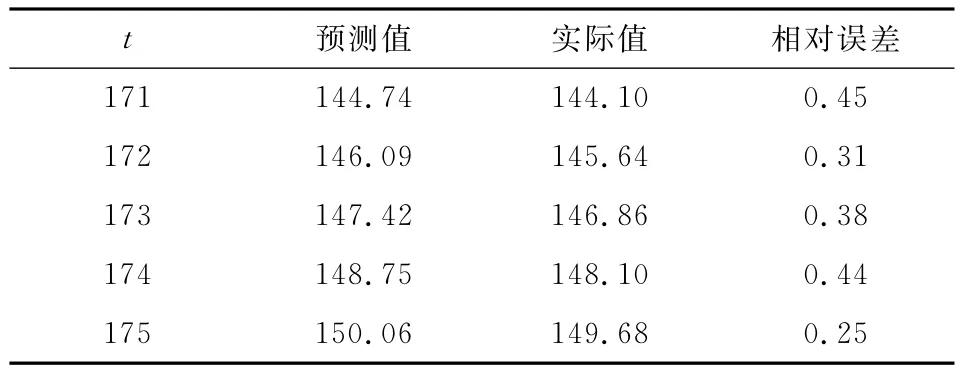
表5 第171－175周的预测值与实际值比较

从表5可以看出，预测结果与实际值的相对误差小于0.5%，说明时间序列模型建模车队失效次数十分有效的.

3 潜在应用

（1）预测未来某时间t的失效次数：如前文所示我们在建立完模型后可以预测车队未来时刻的失效次数，如得到了前175周失效次数的模型，则可以预测之后的失效次数.表6给出了基于前175周数据建模预测的176至180周的累积失效次数.

表6 预测未来五周的失效次数

178 153.98 179 155.29 180 156.60

设一次失效的平均修理费用为Cr＝300（元），停机时间为Td＝1（h），那么在未来i周内的失效总次数、维修费用以及停机时间为：

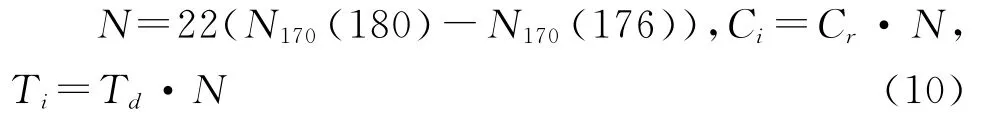
该巴士公司每月制定一次维修计划，如于第175周计算，在未来近一个月（5周）内将有115次失效、需要花费近3.45万元且停机115小时.

（2）预测发生第n次失效时间：假设大修前最优失效次数为160次，则需要估计车队到达160次失效的时间，如本例中到达160次失效时间在第182周，据此则可以安排相应的维修任务.

（3）确定最优大修时间：

根据年龄更换的模型[9]：

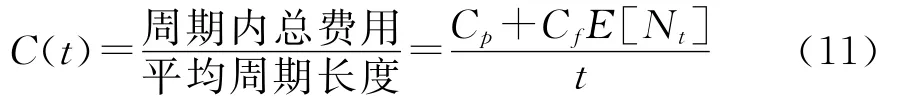
在这里，我们令E[Nt]＝N170，式中Cp＝20000元、Cf＝400元分别为预防维修更换费用和失效更换费用.我们以费用率为目标函数，确定出最优维修时间为to＝127周，费用率变化如图5所示.换句话说，该车队应该在运行到第127周时进行大修.

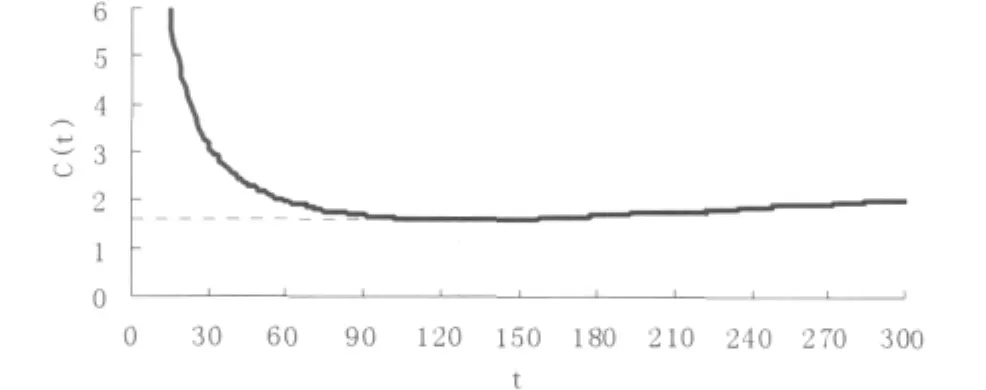
图5 最优大修时间

4 总 结

本文就车队健康管理中的状况预测问题，根据车队数据的特点尝试应用时间序列中法进行分析研究，并结合某车队近175周的失效次数数据给出了应用示例.根据示例研究，我们得到了较理想的结果，验证了时间序列模型在车队健康管理中的适用性.可见，本文是应用时间序列模型于车队健康管理的一次成功尝试.

[1]S.Roe，D.Mba.The Environment，International Standards，asset Health Management and Condition Monitoring：An Integrated Strategy[J].Reliability Engineering and System Safety，2009，94：474－478.

[2]雷 鸣，李学仁，刘林刚.基于 MAS的飞机健康管理专家系统设计[J].微计算机信息，2003：17－19.

[3]杜 隽，王少萍，张文超.航空液压泵源健康管理系统硬件平台设计[J].流体传动与控制，2008，（5）：37－40.

[4]Michael Pecht，康锐.故障诊断、预测与系统健康管理[M].香港：香港城市大学，2010：1－3.

[5]何书元.应用时间序列分析[M].北京：北京大学出版社，2003：1－81.

[6]张树京，齐立心.时间序列分析简明教程[M].北京：清华大学出版社，2003：49－57.

[7]Keh－shin Lii，Tai－houn Tsou.Tests of hidden periodicities in non－Gaussian noise.Workshop Higher－Order Spectral Analysis，1989：83－88.

[8]杨叔子，吴 雅，轩建平，等.时间序列分析的工程应用（上册）[M].武汉：华中科技大学出版社，2007：277－306.

[9]R.Jiang，D.N.Prabhakar Murthy.Maintenance：Decision Models for Management[M].Beijing：Science Press.2008：31－35，102－106.