气液两相流绕管束流动压降特性实验研究

洪文鹏，王宣宇，陈柄君

(1.东北电力大学能源与动力工程学院，吉林 吉林132012;2.长春供电公司，长春130041)

在动力工程、石油化工、核能利用等领域广泛存在气液两相流体绕流管束的流动现象，如冷凝器、蒸发器及核反应堆蒸汽发生器等管壳式换热设备［1-2］。管束间的气液两相流压降特性对其绕流流动特性和传热规律有着重要的影响［3］。因此对换热器管束间压降的准确预测有利于设备的高效安全运行。

目前国内外多位学者对管内气液两相流型、压降、含气率及摩擦系数等进行了大量研究，而对气液两相流体横掠管束流动特性的相关研究较少。Chisholm D［4］研究了两相流水平横掠管束时的流行转变的压降特性，建立了预测流型转变的压降模型。Dowlati R［5］以空气-水为介质研究了管间距对压降的影响，实验发现，Martinelli参数一定时，顺列管束的管间距越大两相摩擦因数越大，而错列管束摩擦因数几乎不受间距变化影响。Schrage D S［6］等人以空气-水为介质研究了影响摩擦因数的因素。以上建立的关联式都在其特定的条件下建立的，适用范围有限。本文对气液两相流绕流节距比分别为1.8和1.3的两种不同管束的压降特性进行研究，并对已有的压降预测模型验证分析。

1 理论模型

本实验中压降实验对比分析所采用的两种模型为。因此对两种模型做简要的介绍。

1.1 一维模型

假定气液两相流绕流管束气液两相充分发展，一维，稳态，绝热。因此，气液两相混合发展的动量方程为

Fsf是管束对流体的作用力，由下式给定

1.2 双流体模型

双流体模型采用多孔介质法(多孔介质是由多相物质所占据的共同空间，是多项物质共存的组合体)进行推导，假定两相流动绝热，稳定，充分发展。假设固体体积份额εs，液体份额，εl，气体份额，εg，则

可用于流动部分的体积分数，即孔隙度是φ=εg+εl=1-εs，对于顺列管束孔隙度为

D是管道直径，P是管间距。因此动量方程为

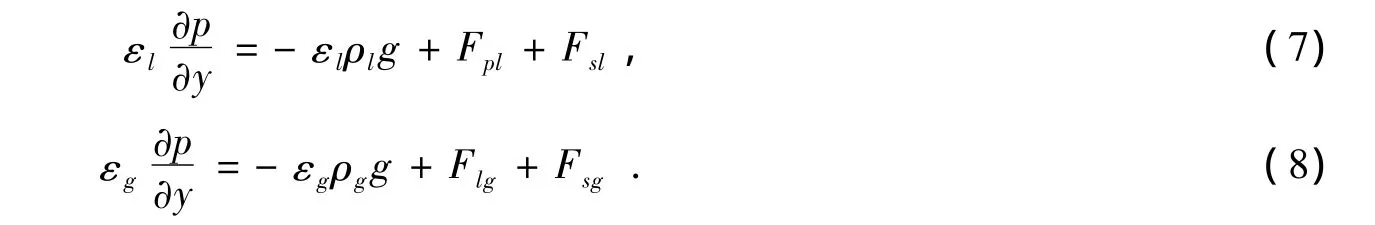
Flg是单位体积液体作用在气体上的作用力，Fsg是单位固体容积作用在气体上的作用了，相应的是单位固体容积作用在液体上的作用力。Flg=-Fgl，由气液动量方程得

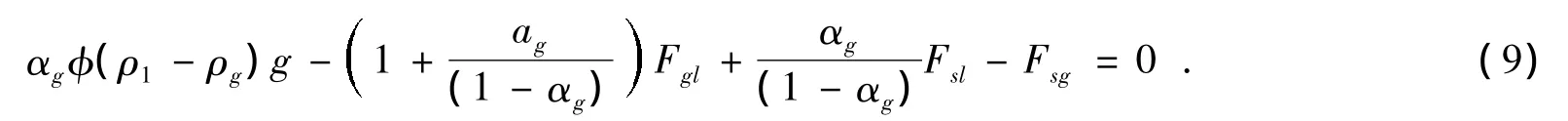
Fsl由液体速度和气体速度相关，

其中:CD为曳力系数，Agl为横断面上所有气泡所占截面积，εg=，带入(10)得

简化后曳力系数计算式为

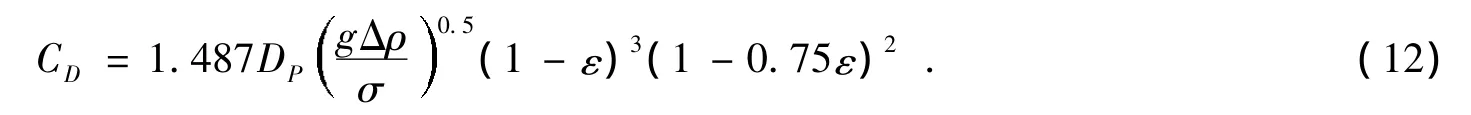
2 实验装置及方法

实验是在空气-水两相流系统上完成的。实验装置如图1所示。该实验装置包括两部分，流体控制系统和动态数据采集系统。流体控制系统主要有空气压缩机、两相混合器、水泵、旋风分离器、水箱及实验段组成。水由水泵抽出，经电磁流量计计量后进入混合器。空气经空气压缩机和气体孔板流量计计量后进入混合器。从混合器流出的气水混合物，流经实验段，进行数据采集后进入旋风分离器，将空气分离出来并排入大气，分离出的水流回水箱循环使用。

图1 实验装置系统图

动态数据采集系统主要有恒压直流电源、压力变送器和数据采集仪组成。采集仪为IDTS-4516U型16通道数据采集仪。压力变送器为Rosemount 3051S电容式压力传感器，测量精度0.05%。实验中动态数据的采集时间为8s，采集频率256 Hz。

图2为实验测试段的管束布置。测试段是由10 mm厚的有机玻璃板制成的长度为700 mm，截面为180 mm×65 mm的矩形通道，分别布置节距比P/D为1.3和1.8的10×4和10×6两种管束。管直径20 mm，长65 mm，采用顺列布置。

图2 测试段管束布置

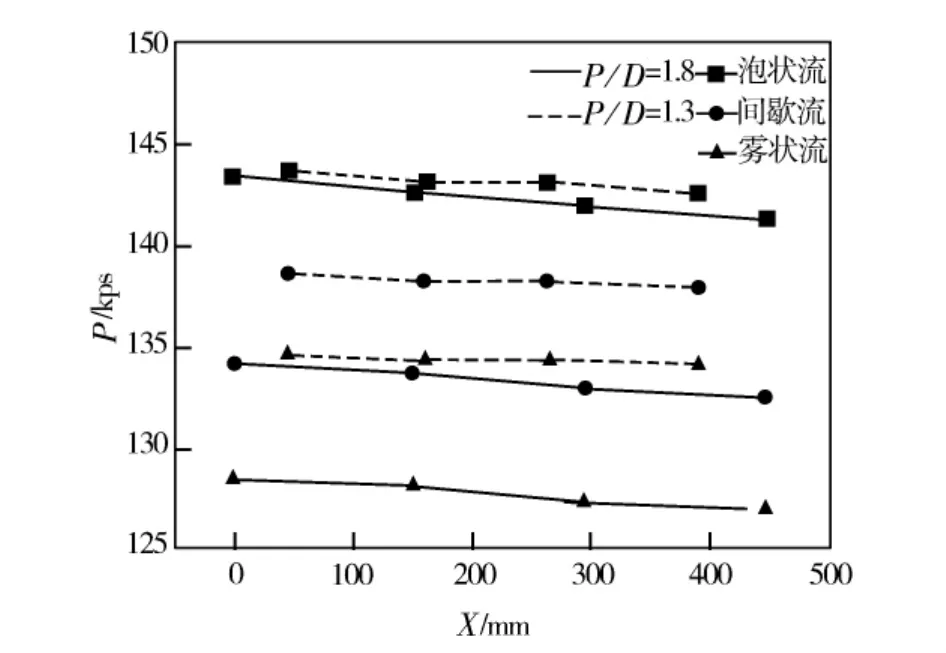
图3 沿管束流动方向的压力降比较

实验中，先调节水流量调节阀，把水流量调到某一流量，再通过调节气体流量来改变流经试验段的总流量和含气率，重复上述步骤直到实验结束。实验参数范围:压力0.1～0.3 MPa，温度10～25℃，水流量2 ～15 m3/h，气流量0.01 ～48 m3/h。

3 实验结果分析

绕流管束时流型主要有三种，即泡状流、间歇流、雾状流。气体以细小气泡的形态分散在液体中流动，气泡尺寸非常小，近似球形或椭球形时的流型称之为泡状流;液弹和气弹连续相随，交替经过管束，中间伴随着气弹的形成和破碎时的流型为间歇流;除了小部分液体粘在管壁或在管束表面形成一层液膜，大部分液体以液滴方式随气流一起流动，这时的流型为雾状流。实验测量了不同流型工况下的压力降，流过管束不同流型压力降如图3所示。实验测得含气率在0.15～0.65之间时，流过两种节距比管束间的压降泡状流最大，间歇流次之，雾状流最小。可能的原因是在气液两相流垂直向上流动过程中，含气率在0.15～0.65范围内，质量流量小时两相压降几乎由重力压降决定(忽略加速压降)，而重力压降的大小与含气率有密切关系，质量含气率小，重力压降大。泡状流的质量含气率最小，所以压降最大，间歇流压降次之，雾状流最小。

将测量压降与一维模型和双流体模型预测值进行比较。一维模型选取三种关联式，分别是Schrage［7］关联式，Dowlati［8］关联式，Feenstra［9］关联式。计算中两相摩擦关联因子由 Ishihara［10］实验所得，单相损失系数由ESUD［11］实验所得。

图4是压降测量值与两种模型预测值的比值随质量含气率的变化趋势。图4(1)显示质量流量为50 kg/m2s时，预测值与测量值接近，而随质量流量的增加，压降预测值与测量值吻合度较差，特别是含气率超过0.3。与双流体模型相比，一维Feenstra模型和Dowlati模型预测压降效果较好，从图4(2)和图4(3)可以看出，随质量流量的增大，其预测数据合理性减小，预测数据偏离实验值。由图4(4)可以看，一维Shrage模型对压降的预测普遍高于实验值，特别是质量含气率大于0.15时，在质量流量为160 kg/m2s时其预测数据进一步偏离实验值。高的压降预测值出现的原因可能是在计算过程中采用的含气率关联式过高的考虑了重力压降的影响，而实际流动过程中其影响较小或有可能不存在。而在大质量流量时，预测数据偏低，可能由于流动过程中的摩擦压降的变化造成的。因此，进一步的工作需要研究大质量流量下的摩擦压降的影响以及修正或建立适用更宽泛的预测模型。

图4 压降比值随质量含气率的变化曲线

4 结 论

本文对气液两相绕流管束的压降进行测量并分析了其压降特性，将实验数据与一维预测模型和双流体预测模型的预测值进行对比分析，发现一维Feenstra模型和Dowlati模型预测效果较好。

［1］Khalid B，David A M.Experimental and numerical investigation of two-phase pressure drop in vertical cross-flow over a horizatal tube bundle［J］.Applied Thermal Engineering，2009，29:1536-1365.

［2］洪文鹏，刘燕，任静秋.顺列管束间气液两相流型及压降特性研究［J］.中国电机工程学报，2011，31(5):84-89.

［3］陈斌，郭烈锦，张西民.管束间气液两相流动特性研究进展［J］.化工机械，1999，26(2):105-109.

［4］D Chisholm，A D K Laird，Two-phase flow in rough tubes［J］.Transactions of ASME，1958，80(2):276-286.

［5］R Dowlati，M Kawaji，A M C Chan，Pitch-to-diameter effect on two-phase flow across an in-line tube bundle［J］.AIChE Journal，1990，36(5):765-772.

［6］Schrage，D S，Hsu，J T，Jensen，M K.Two-phase pressure drop in vertical cross flow across a horizontal tube bundle［J］.AIChE J.，1988，34:107-115.

［7］P A Feenstra，D S Weaver，R L Judd，Improved void fraction model for twophase cross-flow in horizontal tube bundles［J］.International Journal of Multiphase Flow，2000，26(11):1851-1873.

［8］Feenstra，P A，Weaver，D S，Judd，R L.An improved void fraction model for two-phase cross-flow in horizontal tube bundles［J］.International Journal of Multiphase Flow，2000，26:1851-1873.

［9］Z R Simovic，S Ocokoljic，V D Stevanovic，Interfacial friction correlations for the two-phase flow across tube bundle［J］.International Journal of Multiphase Flow，2007，33(2):217-226.

［10］M Ishii，N Zuber，Drag coefficient and relative velocity in bubbly，droplet or particulate flows［J］.AIChE Journal，1979，25(5):843-855.

［11］ESDU，Crossflow Pressure Loss over Banks of Plain Tubes in Square and Triangular Arrays Including Effects of Flow Direction［J］.Engineering Sciences Data Unit，1979，79(34):17.