具有HollingⅡ型功能性反应的捕食者－食饵模型的定性分析

于丽颖

(北方工业学校数学教研室，辽宁盘锦124021)

捕食者－食饵关系是自然界中普遍存在的物种间相互作用的一种基本关系.揭示具有功能性反应的捕食者－食饵相互作用关系，具有非常重要的理论意义和应用价值，许多学者对此作了大量研究工作。1965年，Holling［1］在试验的基础上，对不同类型的物种，提出了三种不同的功能性反应函数，被广泛应用于生物动力系统研究［2－4］。但在已有的工作中，大多假设食饵种群的增长服从经典的Logistic方程

其中，N是t时刻的种群密度，r，k是正常数。Logistic方程假设种群的相对增长率N'/N是种群密度的线性函数，这一假设受到了学者们的质疑［5－7］。

1963年，F E Smith［8］在实验室里利用扩充培养的方法对Daphnia Magna种群进行了研究，发现此种群的相对增长率不满足线性规律，提出了一种形式更为一般、更符合实际的单种群增长模型(称Smith模型或食物有限模型)

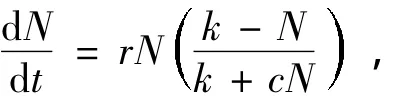
这里r，k，c是正常数，许多学者从不同角度对Smith模型及其各种推广形式进行了深入研究［9－11］。

据悉，文献中对于食饵种群遵循Smith增长和捕食者种群具有HollingⅡ型功能性反应的捕食者－食饵模型至今尚未有学者研究。为此，本文考虑如下自治的具有双密度制约捕食者－食饵系统

其中，x(t)，y(t)分别表示时刻食饵和捕食者的种群密度，系数r，a，b，c，α，β，k，ω均为正常数。系统(1)的建立基于以下假设:

(1)食饵种群:食饵种群的相对增长率(即平均增长率)遵从Smith增长函数h(x)=(r－ax)/(1+kx)，并且满足h(0)=r＞0，h(B)=0，h'(x)=－(a－kr)/(1+kx)2＜0，(0≤x＜+∞，B=r/a)。

(2)捕食者种群:捕食者种群的功能性反应函数φ(x)=αx/(1+ωx)为HollingⅡ型，而β=ea，e表示转化系数，d为捕食者种群的死亡率，b为捕食者种群的密度制约系数。

(3)考虑到r，β分别为系统(1)中的食饵种群和捕食者种群的增长系数，本文总是假设β－dm＞0，d/(β－dm)＜B。

自治的模型(1)具有一般性，其特殊情形在文献中已被广泛讨论。如k=0，m=0即经典的Lotka-Volterra捕食者－食饵系统［12，13］;又如k=0即通常称之谓Rosenzweig－MacArthur模型［14，15］。

1 平衡点的性态

则由

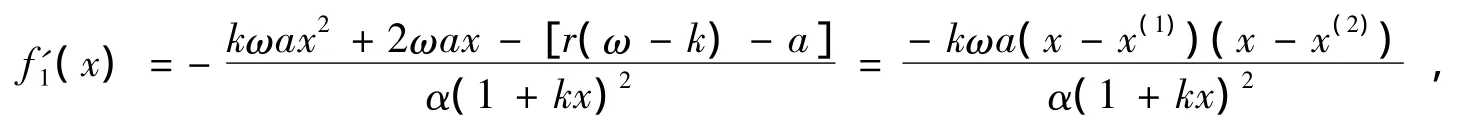
其中

可知x(1)＞0，x(2)＜0，当0＜x＜x(1)时(x)＞0，当x＞x(1)时(x)＜0，得极大点x(1)，记M=f1(x(1))，注意到

由x(1)＜B知在x∈(0，x(1))，f1(x)是凸的上升;在x∈(x(1)，B)，f1(x)是凸的下降。

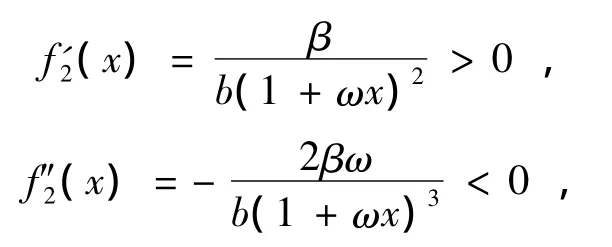
那么系统(1)存在唯一正平衡点Ω(x0，y0)，其中αy0=(1+ωx0)h(x0)，并且

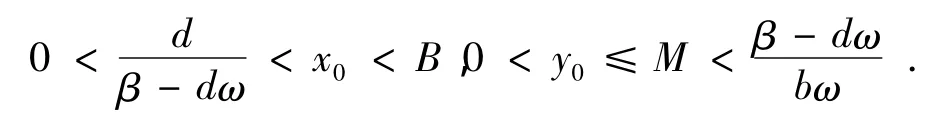
1)在O(0，0)处，系统(1)的线性化系统的系数矩阵为

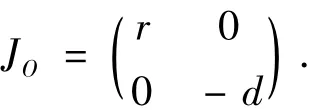
由于detJO=－rd＜0，所以O为系统(1)的鞍点。

2)在E(B，0)处，系统(1)的线性化系统的系数矩阵为

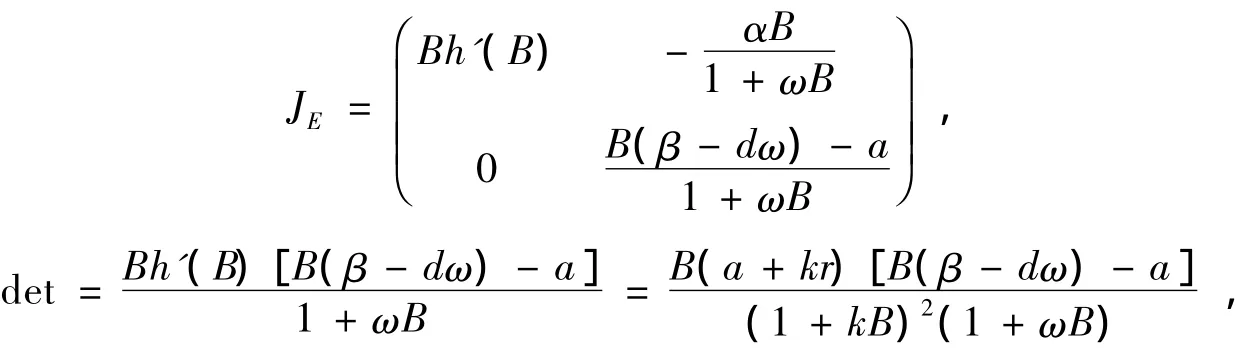
由于B＞d/(β－dω)，detJE＜0，所以E是系统(1)在内的鞍点。

3)在Ω(x0，y0)处，系统(1)的线性化系统的系数矩阵为

这里，N=(1+ωx0)h'(x0)+ωh(x0)，当r(ω－k)－a＞aωx0(2+kx0)时，恒有N＞0成立。注意到，因此

由此，可得如下结论:

①当r(ω－k)－a＞aωx0(2+kx0)且可知Ω是系统(1)在内的稳定焦(结)点;

②当r(ω－k)－a＞aωx0(2+kx0)且知Ω是系统(1)在内的不稳定焦(结)点;

③当r(ω－k)－a＞aωx0(2+kx0)且，则由文［8］定理4.3知Ω是系统(1)在内的中心－焦点型奇点。

引理1非负平衡点O(0，0)和E(B，0)是系统(1)的鞍点，对于正平衡点Ω(x0，y0):

①当r(ω－k)－a＞aωx0(2+kx0)且时，Ω是系统(1)的稳定焦(结)点;

②当r(ω－k)－a＞aωx0(2+kx0)且时，Ω是系统(1)在的不稳定焦(结)点;

③当r(ω－k)－a＞aωx0(2+kx0)且时，Ω是系统(1)在内的中心－焦点型奇点。

证明设x1=max{，B}作直线l1:x－x1=0，即x=x1，当x1=B时，由系统(1)得

当x1=时，表明＞B(即r－a＜0)，由系统(1)得

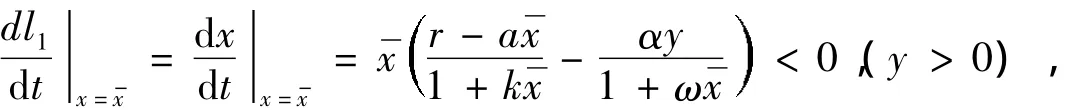
这表明系统(1)的正半轨线经直线l1时是自右向左的;

可见，系统(1)的正半轨线经直线l2时是自上向下的;

又直线l3:x－0=0及l4:y－0=0都是系统(1)的轨线，因此由l1，l2，l3，l4构成的闭合曲线Γ所围成的区域是系统(1)的最终有界区域。证毕。

2 闭轨线的不存在性

定理1如果2b＜α≤4b且2b(rω+α)＞αa，则系统(1)在内不存在闭轨线

证明作Dulac函数:B(x，y)=x－1y－1，于是，由系统(1)及∀(x，y)∈，有

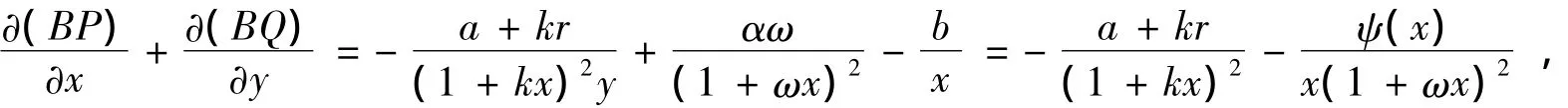
其中ψ(x)=b(1+ωx)2－αωx，由于

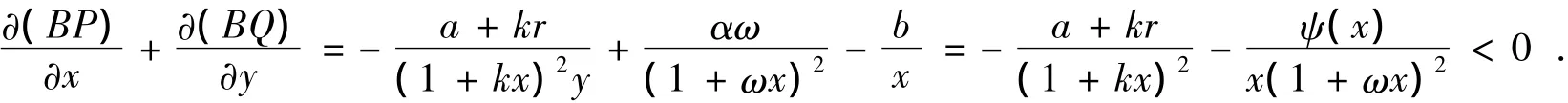
定理2设系统(1)满足定理1条件，又同时满足条件

证明由引理1、引理2和定理1易得，证略。

3 极限环的存在唯一性

首先，我们讨论系统(1)极限环的存在性:由引理1知，Ω(x0，y0)是系统(1)的不稳定焦(结)点。今作包围不稳定焦(结)点Ω(x0，y0)的闭区域:

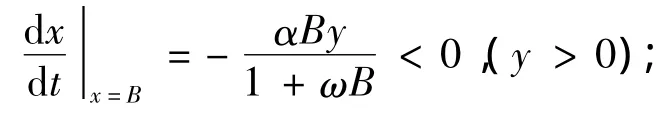
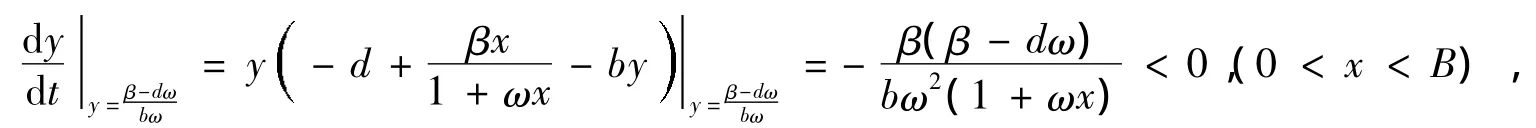
③直线x=0及y=0，即正半y轴和正半x轴都是系统(1)的轨线。

再证唯一性:作自变数变换:(1+ωx)dτ=dt，则将系统(1)化为下面等价系统

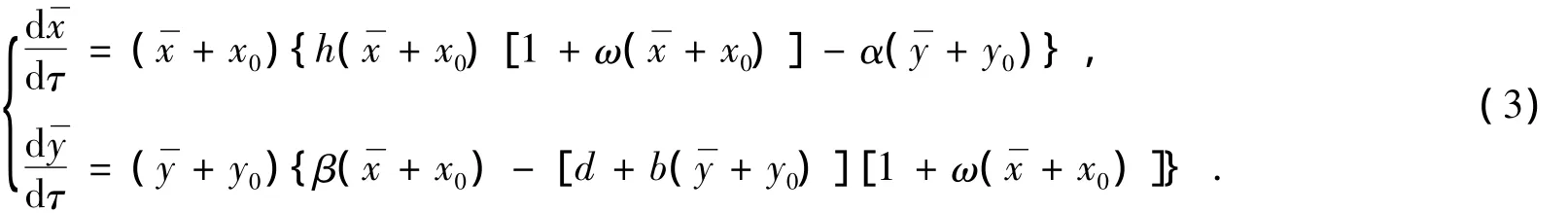
再令αy0exp{b［ωx0(eu－1)+u］/α}dτ=ds，变换后u，υ，ds仍记为x，y，dt，进而将系统(1)化为Lienard系统

其中

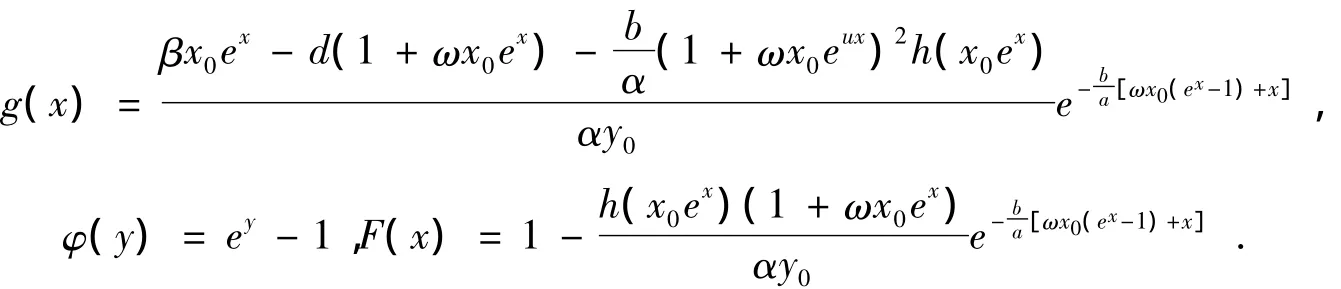
由上述所使用的一系列变换可知，系统(1)的正平衡点Ω(x0，y0)变为Lienard系统(6)的平衡点O(0，0)，为此，相应地需要证明Lienard系统(6)在包含有平衡点O(0，0)的带状区域－∞＜x＜ln{B/x0}内，至多存在一个极限环。

由系统(1)在带状区域0＜x＜B内存在唯一正平衡点Ω(x0，y0)知

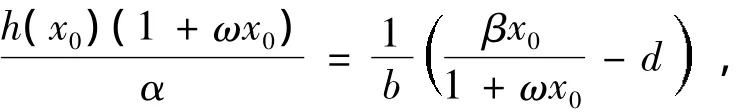
据此，H(x)=0存在唯一正根x0使得H(x0)=0，当0＜x＜x0时，即f2(x)＜f1(x);当x0＜x＜B时，f2(x)＞f1(x)，即H(x)＞0。

①由所使用变换知，当0＜x＜B时，对应系统(6)中－∞＜x＜ln{B/x0}，当0＜x＜x0时，H(x)＜0，ln{x/x0}＜0，对应于－∞＜x＜0，xg(x)＞0;当x0＜c＜B时，H(x)＞0，ln{x/x0}＞0，对应于0＜x＜ln{B/x0}，xg(x)＞0.因此，x≠0，xg(x)＞0.

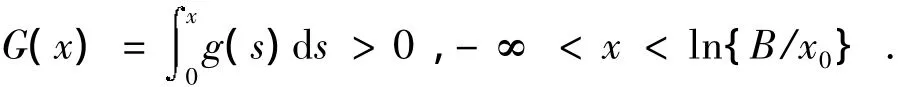
②y≠0，yφ(y)=y(ey－1)＞0，φ(－∞)=－1，φ(+∞)=+∞，并且φ'(y)=ey＞0，φ(y)是单调增加的。

③由前面讨论知αy0=(1+ωx0)h(x0)，所以F(0)=1－1=0，在条件

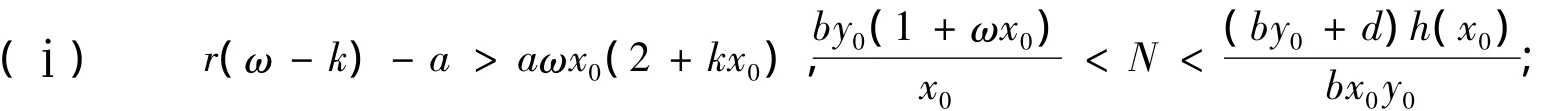
当－∞＜x＜ln{B/x0}且x≠0时，相应于系统(1)0＜x＜B且x≠x0，则当条件

成立时，恒有

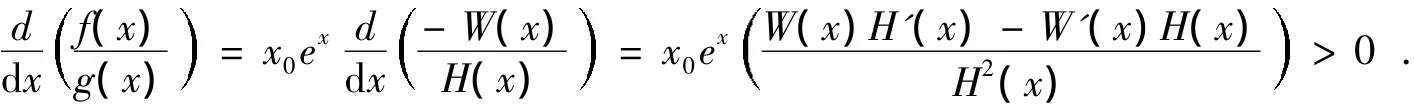
综上，根据张芷芬唯一性定理［16］获得如下定理3。

定理3如果系统(1)满足条件

6 结论

本文所研究的食饵带有Smith增长的捕食者——食饵模型，具有重要的理论意义和实际应用价值。当参数满足定理2条件时，捕食者——食饵两种群将长期共存并稳定在一组恒正的定值上;当参数满足定理3条件时，捕食者——食饵两种群将产生生物性周期振荡现象，并将趋于稳定的。这一结果不仅揭示了该生态系统在食物有限时的基本演变规律，而且在控制理论中也有其重要学术价值。

［1］Holling C S.The Functional Response Predators to Prey Density and its Role in Mimicty and Population Regulation［J］.Mem Ent Sci Cannad，1965，97(45):5－60.

［2］匡亦群，邱梅青.一类具功能反应的食饵－捕食者模型的定性分析［J］.生物数学学报，2007，22(4):629－633.

［3］Jicai Huang.Bifurcation and Chaos in a Discrete Predator-Prey System with Holling Type-ⅣFunctional Response［J］.Acta Math.Appl.Sinica，English series，2005，21(1):157－176.

［4］田德生，朱长青，朱永松.HollingⅣ捕食－食饵时滞系统的多个周期解［J］.纯粹数学与应用数学，2009，25(2):339－345.

［5］黄健民.食饵按广义生长的HollingⅡ型功能反应的捕食者－食饵模型［J］.华南师大学报，1996(4):90－95.

［6］Fan M，Wang K.Global Existence of Positive Periodic Solution of a Predator-Prey System with Holling Type II Functional Response［J］.Acta Mathematiea Scintia，2001，21(4):83－91.

［7］Li Y K.Periodic Solutions of a Periodic delay Predator-Prey System［J］.Prie of Amer Math Sec，1992，127(5):1331－1335.

［8］Smith F E.Population Dynamics in Daphnia Magna and a new Model for Population Growth［J］.Ecology，1963，44(4):651－663.

［9］孙伟平.微分方程边值问题的若干研究［D］.北京:北京理工大学论文，2000:65－68.

［10］Lotka A J.Elements of Physical Biology，Williams and Wilking Baltimore［M］.New York:Reissued as Elements of Mathematical Biology，Dover，1956.

［11］Volterra V.Variazienie Fluttuazini Del Numere in Specie Animali Conviventi［M］.Mem Res Com Tolassogr Ital，1927.

［12］Lotka A J.Elements of Physical Biology，Williams and Wilking Baltimore［M］.New York:Reissued as Elements of Mathematical Biology，Dover，1956.

［13］Rosengzweig M L.Why the Prey curve has a Hump［J］.The American Naturalist，1969，103(929):81－87.

［14］陈兰荪，井竹君.捕食者－食饵相互作用微分方程的极限环存在唯一性［J］.科学通报，1984，24(9):521－523.

［15］张芷芬，丁同仁，黄文灶.微分方程定性理论［M］.北京:科学出版社，1985，152－153.