基于分治法的高校考试安排算法

骆绍烨

（莆田学院电子信息工程系，福建莆田 351100）

0 引 言

现代教育理论认为，考试是教育评价的一种重要手段，其作用主要表现在以下两个方面：其一是评估教师的课堂教学效果，促使教师总结教学经验，改进教学方法；其二是评价检测学生的学习效果，了解学生对所学知识和技能的掌握情况和应用能力，促使学生学习以及帮助改进学习方法［1］。

传统的考试安排方式主要是依靠教学管理人员的人工安排，虽然他们在考试安排中逐渐积累了一些经验和方法［2］，但是，随着专业的不断增加和细化，组织考试的工作量越来越大［3］，而且组织考试的时间大多是在学期中或学期末，此时教学管理的工作又相对集中，时间有限，任务又重，人工管理的方式暴露出了不少的弊端。

计算机自动排考是一个时间表问题，把考试安排问题化为计算领域有约束的时空组合优化问题进行求解［4］。由于约束条件复杂，问题规模庞大，对于排考这类问题迄今为止还没有找到在多项式步骤内解决的有效算法，只能在一定范围内寻求最优解。

1 排考问题描述

从排考过程中涉及到的可能引起潜在资源竞争冲突的角度，排考问题涉及到的因素主要有：时间、课程、场地、班级和教师。其中班级又分为行政班级和考试班级。行政班级指招生时注册的班级，每个行政班级有编号、名称、院系、专业和学生人数。每个行政班同一时间只能考一门课程。考试班概念的产生主要是基于有些课程由于人数过多或者其它原因需要拆班考试。

1.1 约束条件

排考的约束条件可分为两大类：硬约束和软约束。

1．1．1 硬约束

硬约束表示必须遵守的约束条件。

硬约束主要包括以下几个方面：

1）同一班级在同一时间不能考两门不同的课程。

2）同一教师在同一时间不能安排两个考场。

3）同一考卷的班级应在同一时间安排考试。

4）考场的容积必须大于在该处考试的学生的人数。这里所说的容积不是考场的总座位数，而应指按照考试要求所能排下的最大学生数。

5）安排监考的教师必须在岗。

1．1．2 软约束

软约束表示在排考过程中尽可能满足的约束条件，但不满足也无妨，软约束条件的满足与否往往与排考实际情况有关。

软约束主要包括以下几个方面：

1）该课程的授课教师应参加监考，且尽可能安排在该教师所授课班级监考。这样可以方便解决考试中出现的诸如试卷不清等问题。

2）课程安排有一定间隔，让学生有足够备考时间。一天内一个班级尽可能只安排一门考试。

3）教师安排监考次数适当。

4）满足监考教师监考意愿偏好。

5）在指定时间段内安排考试。

1.2 排考目标

由约束条件可以看出，对于排考问题实际上是一个组合规划问题，但要求出问题的最优解却是不可能的，虽然约束条件能帮助我们进行求解，但是随着问题范围的扩大，组合方案呈爆炸式增长，特别是高校的排考问题，其排考难度更大［5］。因而，我们必须放弃寻求最优解，事实上，迄今为止，对排考和排课问题的研究也证明了最优解是极难求出的，只能“退而求其次”，寻找问题的近似最优解。只要这个解能够在满足硬约束条件的前提下，尽可能地满足软约束，满足各方面的需求，使得解决方案合理可行。

2 系统自动排考算法设计

随着资源数量的增大，排考问题因考试编排选择方案的剧增，就可能出现“组合爆炸”，致使排考问题变得错综复杂，从而直接影响到排考问题的解［6］。为了降低排考算法的复杂性，在自动排考时运用分治法的思想，将问题空间分解成多个小规模空间，分别求出各个小空间的解，再组成整个问题的解的方法。

分治法的思想就是将整个问题分成若干个问题后分而治之［7］。当要求解一个输入规模为n，且n取值又相当大的问题时，直接求解往往是非常困难的，有的甚至根本没法直接求出。每当遇到这类问题时，分治法往往能发挥很大的作用。任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少［6］。

运用分治法解决排考问题，把问题空间逐层分解成多个小规模空间，可以减小问题规模。排考时，先将课程分成公共课与专业课两种类型，因为公共课与专业课有着各自不同的特点。公共课课程数量少，但参加考试的班级较多，而专业课则恰恰相反。将两种课程类型分开，有利于采取不同的分配方案，同时也降低了问题的规模。其次，在专业课排考时，将整个学校的考试安排调度分解成各个开课院系的考试安排，问题空间再次缩小。最后将排考过程分解成安排时间、安排场地和安排监考老师3个相对独立的子问题。安排时间时，只需要考虑课程与时间的搭配；安排场地时，只需考虑考试班级与考试场地的搭配；安排监考教师时，只需保证监考教师的监考时间不冲突即可。由以上可以看出，在逐层的分解过程中，求解的难度也不断降低，排考得到了更简单和更迅速的求解。分解到位的排考算法主要通过以下步骤实现。

1）选取课程。为了减少排考过程中可能出现的冲突，采取先难后易的原则，不好安排的课程先排，即容易在排考时出现冲突的、排考条件要求较难满足的课程优先进行排考。如果这些课程在排考后期才开始安排，此时很多资源已被占用。因为虽然总的资源数量是一定的，但到了排考的后期，剩余的资源特别可能会出现类似存储管理中的资源碎片问题，即大量空余的资源很少，取而代之的是分布零散的资源碎片。这时为这些较难安排的课程寻找到适合的资源就变得更难了，也就影响了排考的顺利进行。排考过程中，课程的参加考试班级数、参加考试班级的人数、参加考试班级的考试课程数等多个因素都会影响课程的考试安排难度，但影响最大的因素还是课程的参加考试班级数。

2）贪心法安排时间。选定待排考课程之后，接着就是为课程安排考试时间，公共课的考试时间由排考人员直接指定，专业课程的考试时间在计算机自动排考时是由系统根据权值法和贪心法选定。

在安排专业课程考试时，排考人员首先需要计算每个可排考时间的权值。管理员可以根据需要将一天的考试时段分成1～5个不等的时间段。将所有可以排考的时段的权值存放在权值数组periodstate［］中，periodstate［X］表示第X个时间段的权值。当我们需要表示考试安排区间中的第M天的第L个时段的权值时，有如下公式：

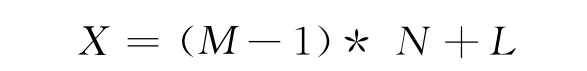
式中：N——每天可排考的时段数。

在为课程选择考试时间时，首先初始化时段权值数组，将所有的考试时段的初始权值为同一值10 000。然后逐时段分析计算各个考试时段的权值。权值的计算方法如下：

首先，如果该时段排考课程中的任何一个参考班级在此时段已安排了考试，则该时段的权值为0。其次，为了使得软约束中的要为学生留有一定的备考时间的条件尽量得到满足，一个班级尽可能不在一天安排多场考试，即一天在可能的情况下最多只安排一场考试。因此，检查该天是否有班级已安排了考试课程，如果有，每增加一个已在该天安排了考试课程的班级，则相应地降低该时段的部分权值。

在使用权值的计算办法处理完所有时段的权值后，就可以使用贪心策略来选择课程的考试时间了。贪心法是一种改进了的分级处理方法，就是在对问题求解时，总是做出在当前看来是最好的选择，每一步都应是局部最优解，不从整体最优上加以考虑，所做出的仅是在某种意义上的局部最优解［8］。贪心法通过不断求解局部最优解逐步构造全局解的方式，对许多问题可以产生整体最优解，即使不能得到整体最优解，也能找到最优解的较好的近似解。并且排考问题实际上并不一定需要找出整体最优解，排考问题最优解的定义也是个难题。所以在很大程度上，只需要求得一个次优解或者满足解即可。在安排课程考试时间上采用贪心法，能在保证速度的前提下求得局部最优解，符合速度和效用的平衡，从而获得整体最优解的良好特性，进而使其在排考系统的应用中能够发挥其主要的特性。

3）最佳适应法安排场地。最佳适应算法（Best Fit）是动态存储分配解决方案中最为常见的一种方案。最佳适应算法就是在内存空间中为将要加入的作业选择大于该作业需要的空间大小，并且是最小的内存空间来存放该作业［9］。排考时的安排考试场地与模拟内存分配十分类似，可以模拟其分配方式。

安排考试场地，首先必须从数据库中获取在排的考试班级的人数K，接着从数据库中获取属于开考班级院系且容积大于K的所有考试场地的信息，然后逐个考试场地进行比较选择。比较选择时，在确定考试场地在安排的课程考试时间时是空闲的情况下，计算考试场地容积S与班级人数K的差值，与已有的场地中的容积与班级人数之差的最小值MIN（S－K）做比较。如果当前的S－K值更小，则记录下当前的考试场地编号和新的MIN（S－K），否则直接选取下一个场地。如此判断比较直至比较完所有的考试场地，此时记录的考试场地即是算法所求的场地。

4）等概率分配法安排监考教师。在安排了考试的时间和考试场地之后，最后要做的是安排监考教师。依据高校的有关考试规定，每个考场安排两位监考教师监考。监考教师原则上选取学生所在系的教师。在安排监考教师时应考虑教师的在岗情况及监考意愿。同时，在满足教师监考意愿的前提下，应考虑教师工作量的均衡，因而对于可任意参加监考的教师使用等概率分配法来安排监考教师。为了方便解决考试中可能出现的一些问题，在安排监考时，优先安排授课教师参加监考，如果该授课教师还未被安排监考，则将其安排到他所担任课程的班级监考。然后获取所有在岗且愿意参加监考的教师信息，以相同的概率分配监考任务。

3 结 语

排考问题是一个有约束的、非线性的、模糊多目标优化的、难解的、时空组合的数学问题［4］。目前还没有找到在多项式步骤内解决的有效算法，只能在一定范围内寻求最优解。根据高校的具体实际所设计的排考算法实现较容易，求出解的合理性也较高，能适应大部分高校排考系统算法设计的要求。

［1］ 朱菊芳．高等教育学教程［M］．南京：南京师范大学出版社，1995．

［2］ 王玲．分布估计算法在排考中的应用［D］：［硕士学位论文］．长沙：湖南师范大学，2008．

［3］ 李红，陈晏辉．高校课程考试管理的思考［J］．长春工业大学学报：高教研究版，2008，29（4）：31－32．

［4］ 张磊，张博锋．分组遗传算法优化大学考试时间表［J］．计算机工程与应用，2009，45（23）：236－238．

［5］ 胡荷芬．高校考试自动安排算法研究和系统设计［D］：［硕士学位论文］．上海：上海师范大学，2008．

［6］ 唐洪英，周敏．基于分层次、贪心算法的排课系统的设计与实现［J］．微计算机信息，2006，22（3）：237－240．

［7］ 胡峰，王国胤．基于分治法的快速确定规则获取算法［J］．模式识别和人工智能，2010，23（3）：349－356．

［8］ 常友渠，肖贵元，曾敏．贪心法的探讨与研究［J］．重庆电力高等专科学校学报，2008，13（3）：40－42．

［9］ 宗大华，宗涛，陈吉人．操作系统［M］．北京：人民邮电出版社，2009．