PID广义预测控制在分子蒸馏中的应用

隋添翼， 李云鹏， 于欢欢， 张 洋， 许红岩

（长春工业大学电气与电子工程学院，吉林长春 130012）

1 概 述

广义预测控制（Generalized Predictive Control）是20世纪80年代产生的一种新型控制方法，是预测控制中最具代表性的算法之一。通过在线辨识获得模型参数，再利用模型参数实现多步预测和滚动优化的自适应模型预测控制算法，由于其具有保持最小方差自校正控制的模型预测、最小方差控制、柔化作用、在线辨识等特征［1－2］，使GPC对建模误差和外界干扰等未知因素具有很强的适应能力。为了获得更好的控制效果，在目标函数中使用了控制增量序列，使它适用于大延迟、非最小相位以及非线性等过程。但是对于一些既含有较大建模误差，又含有较大外界干扰的复杂工业控制过程，就会产生预测输出与实际输出相差甚远等现象。另外，GPC也有在线计算量大、超调难以抑制等问题。

在工业过程控制中，PID控制应用最为广泛，约占生产装置控制回路总数的80%～90%，其控制器的控制规律为比例（P）、积分（I）和微分（D）。具有原理简单、直观易懂、鲁棒性强、可靠性高、易于工程实现等一系列优点。但是像在分子蒸馏提纯五味子油生产中的真空度、蒸发温度、薄膜厚度控制对象，它具有非线性、大惯性、纯滞后等特点，容易引起系统超调和持续的振荡，并且温度、真空度控制对象的参数一般会发生较大的变化，加上对象模型参数随工况参数的变化而变化，具有非线性、时变不确定性，因此，应用单一的PID控制很难达到精确控制的目的。

为使控制系统的反馈环节兼顾鲁棒性和抗干扰能力，利用PID和GPC这两种控制方法的优点是改造目标函数，将广义预测控制算法的性能指标构造成PID形式，获得一种能抑制超调的、具有PID结构的预测控制算法。

通过分子蒸馏提纯五味子油的实验，说明了PIDGPC算法的控制性能，并分析了各PID参数对系统性能的影响。

2 分子蒸馏

2.1 分子蒸馏基本原理

分子蒸馏是一项国内外正在进行工业化开发应用的高新液－液分离技术，它突破了常规蒸馏依靠沸点差分离物质的原理，是在133．3×10－2～133．3×10－4Pa的高真空下进行分离操作的非平衡蒸馏过程，在此条件下蒸发面和冷凝面的间距小于或等于被分离物料的蒸气分子的平均自由程，所以又叫短程蒸馏（Short－pathdistillation），其基本原理是利用不同种类分子逸出液面后，其平均自由程不同的性质来实现分离的。分子蒸馏原理如图1所示［3］。

液体混合物的分子沿着加热板自上而下流动，当获得足够的能量时，轻、重分子就会从液面逸出而成为气体分子。由于轻重分子的平均自由程不同，轻分子自由程比重分子的自由程要大，在大于重分子平均自由程而小于轻分子平均自由程处设置一冷凝面，使得轻分子不断地被冷凝收集，重分子由于不能到达冷凝面而在气相中饱和，并返回蒸发面沿蒸发面馏出，达到轻、重分离的目的［4］。

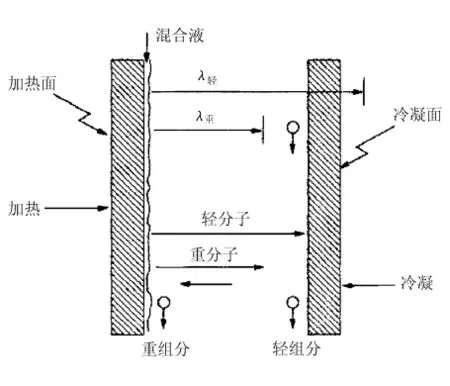
图1 分子蒸馏原理示意图

2.2 分子蒸馏的技术理论

2．2．1 分子平均自由程

一个分子在相邻两次分子碰撞之间所经过的路程称为分子运动自由程，在某时间间隔内自由程的平均值称为平均自由程［5］。设某一分子的平均速度为Vm，碰撞频率为f，λm为平均自由程。则

由热力学原理可知：

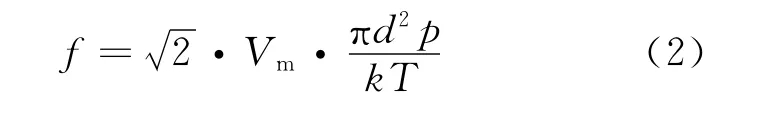
所以

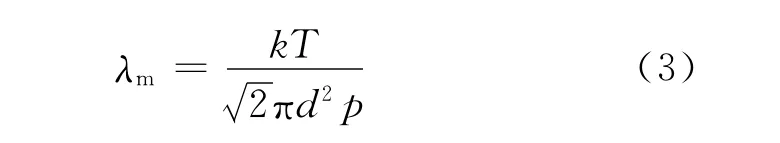
2．2．2 蒸发速率

分子蒸发速率是衡量分子蒸馏设备工作效率的一个重要标志［6］，Lutisan对双组分理想物系的刮膜分子蒸馏器内的传质和传热情况进行数学建模。

根据Navier－stokes方程建立了在y方向上j表面的速度方程：

在忽略蒸气相中分子间碰撞影响的情况下，得到总的蒸发速率方程：

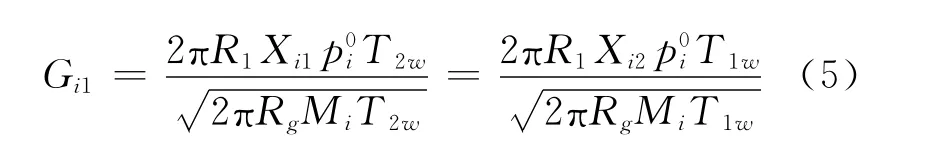
2．2．3 热分解

Hichman对分解概率给出以下公式［7］：

其中，停留时间取决于加热表面长度、物料黏度、表明载荷和物料的流量，通过分解概率可以看出物料的热损伤。

3 广义预测PID控制器设计

3.1 广义预测控制

随着广义预测控制（GPC）在工业过程控制中的广泛应用，广义预测控制的研究已成为当前自动控制工程界研究的热点。GPC作为一种新型的远程预测控制方法，集多种算法的优点为一体，是一种通过在线辨识获得模型参数，再利用模型参数实现多步预测和滚动优化，并且保持最小方差自校正控制的模型预测、最小方差控制等原理基础上而发展起来的一种自适应模型预测控制算法。其控制系统框图如图2所示。

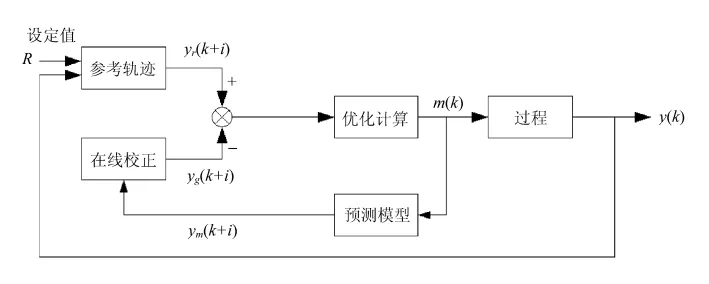
图2 GPC系统结构图

3.2 基于CARIMA模型的广义预测控制

用“被控自回归积分滑动平均模型”来描述受到随机干扰的对象［8］。

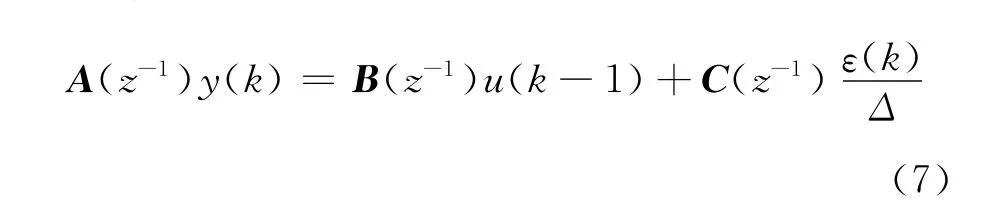
其中：

式中：y（k），u（t）——分别表示系统的输入和输出；

Δ＝1－z－1；

｛ai｝，｛bi｝，｛ci｝——分别为A，B，C3个多项式的系数；

na，nb，nc——对应的阶次；

A，B，C——向量。

为导出利用当前时刻k及以前的输入和输出数据预测k＋j时刻的j步导前输出，引入一组Diophantine方程，并令C（z－1）＝1。

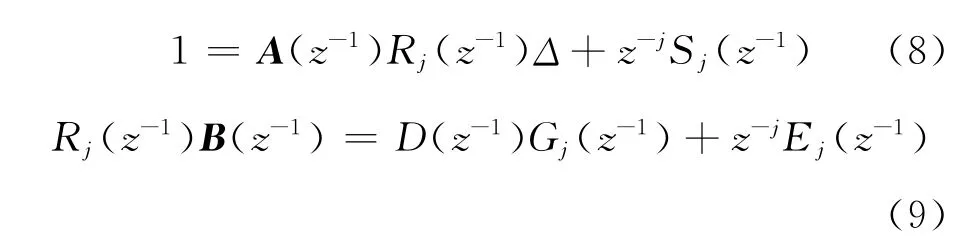
可得系统的j步预测输出为：

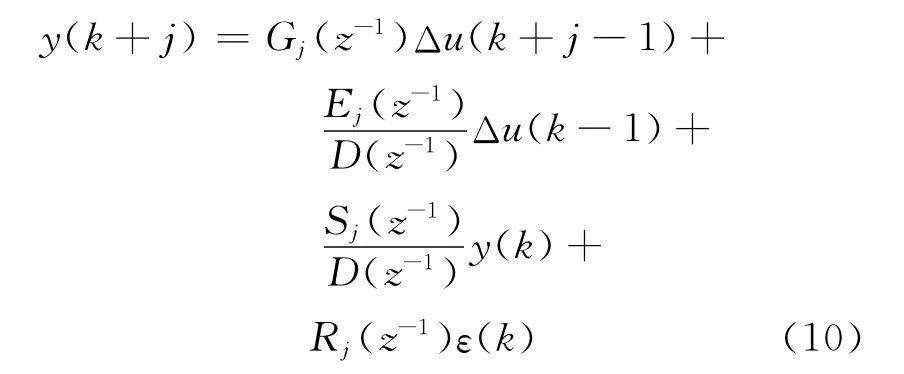
修正后的最优j步预测输出为：

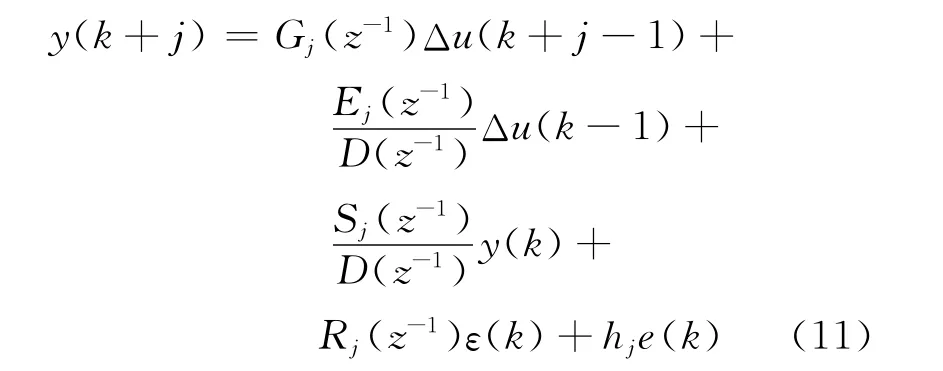
当预测步数j改变时，需要用递推解法重新计算式（10）和式（11）。因为多项式Rj（z－1），Sj（z－1），Gj（z－1），Ej（z－1）的相关参数将于预测步数j一起变化。M为控制时域，当j＞M时，预测步数j取从1到P，则Δu（k＋j－1）＝0，可用下式计算其多步输出的预测值：

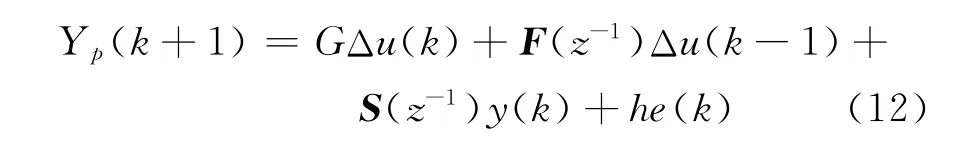
由此可得，GPC的最优控制率为：

式中：P——最大预测步数；

M——控制时域长度；

qj——输出误差加权系数，通常可以取为常量；

λj——控制量的加权系数，通常可以取为常量。

输入的参考轨迹为yr（k＋j），可由下式求得：

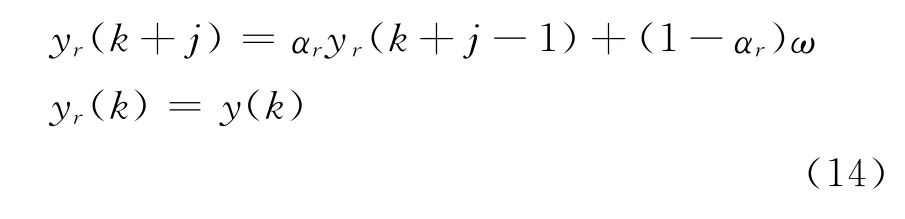
由式（14），并将式（13）写成矢量形式可得：

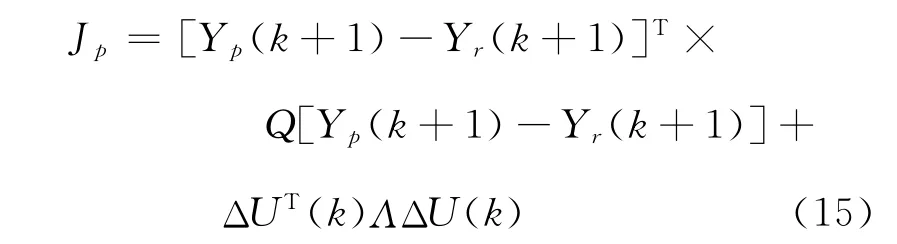
对式（15）进行关于ΔU（k）极小化运算可得：

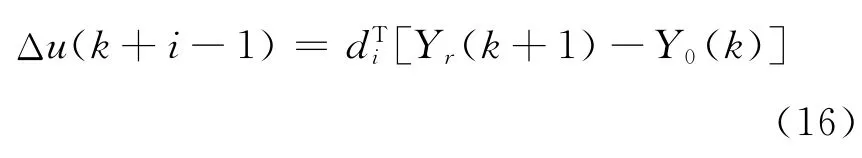
3.3 PID型的广义预测控制

PID型的广义预测控制是指具有PID结构的广义预测控制，原始的GPC函数为：

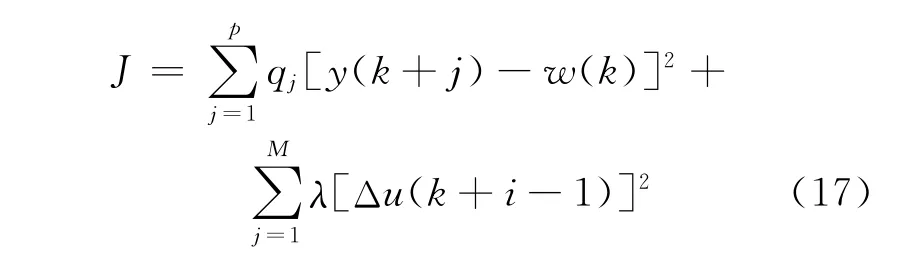
输出误差可取为｛e（k＋j）｝，并令：

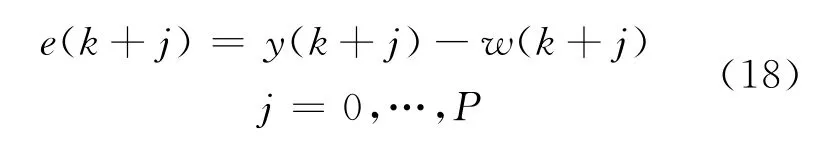
则可得性能指标为：

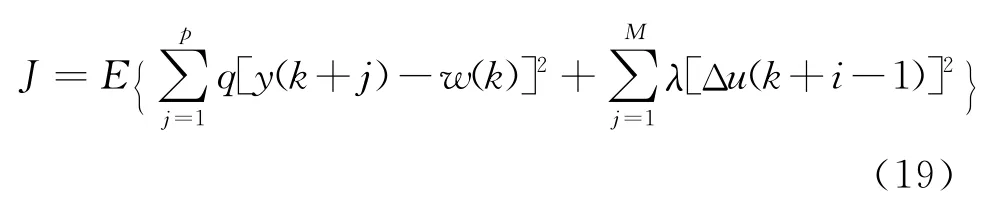
用Δ分别乘以式（19）的两边后可以得到：

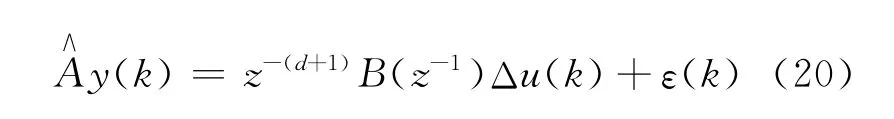
求解下面的Diophantine方程：

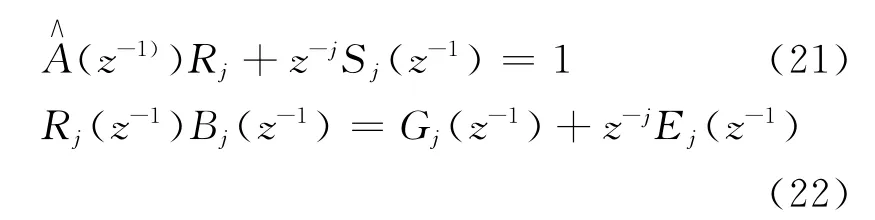
取

可得：

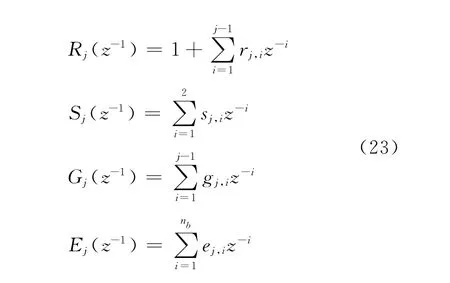
由下式计算可得pj：

其中，G包括了Gj（z－1）系数。

修正式（19）的性能指标，可以得出其最优控制法则：

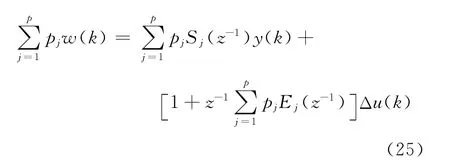
取

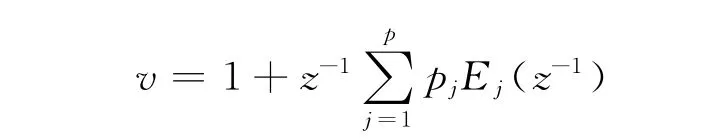
用v除以式（25）的两边，计算后可得到：

因为：

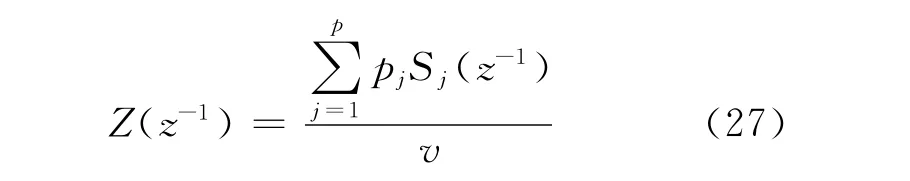
并且由PID算法：

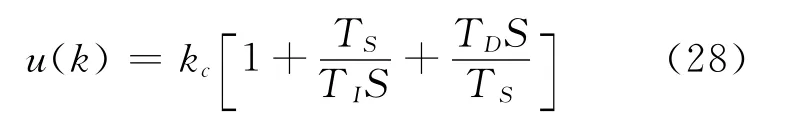
可以得出：

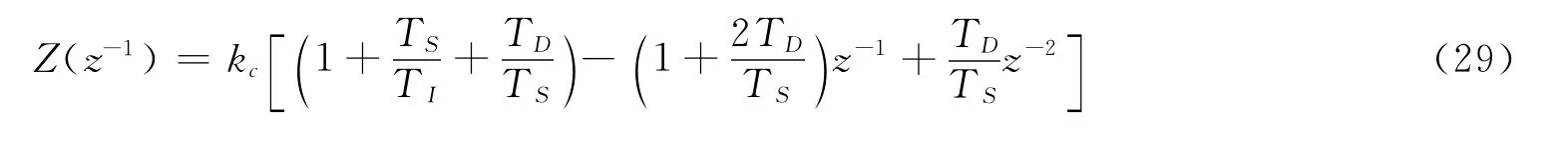
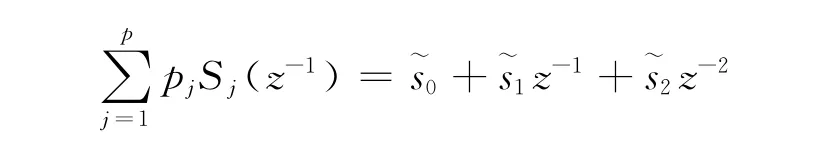
联立式（29）和式（30）可以推出广义预测控制的PID参数：

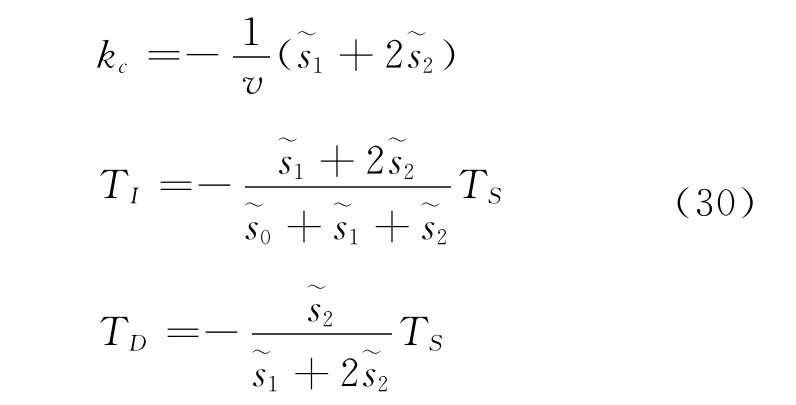
将推出的kc，TI和TD代入下式：

即可得输出增量。具有PID结构的广义预测控制的系统框图如图3所示。

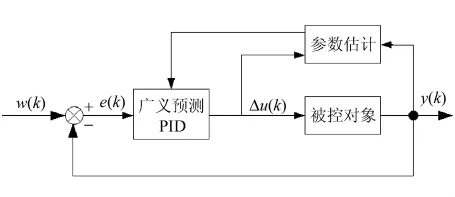
图3 PIDGPC系统结构图

4 实验仿真

仿真对象为刮模式分子蒸馏器，具有PID型的广义预测控制与广义预控制的仿真结果对比如图4所示。

图4 PID与PIDGPC比较

选取α＝0．8，λ＝5，Ki＝8，Kp＝12，Kd＝2。通过对PIDGPC的3个参数Ki，Kp，Kd的调节，可以看出，改进后的PIDGPC算法具有良好的动态性能，其对系统超调的抑制和保持稳定性等方面都有了明显的提高。

Ki，Kp，Kd的变化对系统性能的影响如图5～图7所示。

图5 Ki对系统输出的影响

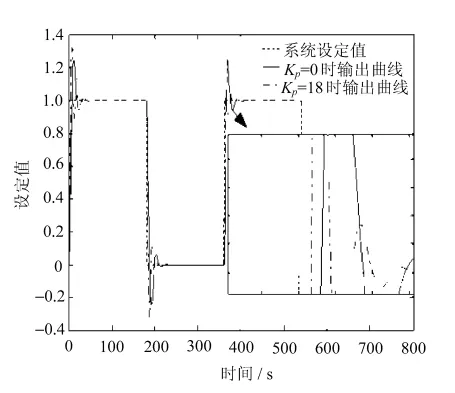
图6 Kp对系统输出的影响

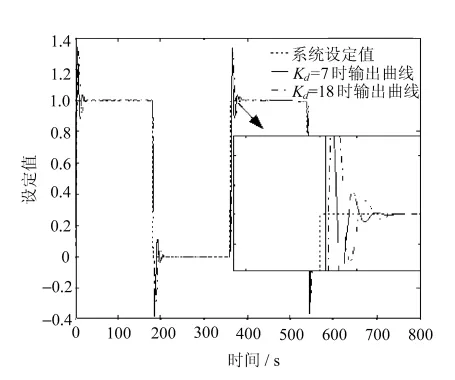
图7 Kd对系统输出的影响

图5中，选取α＝0，λ＝5，Kp，Kd保持不变，分别为5和12。通过改变Ki的值可以看出，当Ki增大时，系统的超调增大，但是其动态性能和响应速度得到了提高。

图6中，选取α＝0，λ＝1，Ki，Kd保持不变，分别为8和2。通过改变Kp的值可以看出，当Kp增大时，系统的超调增大，但是其动态性能和响应速度得到了提高，稳定性下降。

图7中，选取α＝0，λ＝1，Ki，Kp保持不变，分别为8和12。通过改变Kd的值可以看出，当Kd增大时，系统的动态性能和响应速度下降，但是其超调的抑制效果增强，保持系统稳定性。

5 结 语

通过仿真结果研究发现，PIDGPC控制器具有广义上的比例、积分、微分的结构特征，其控制参数可以随着控制对象状态的变化而改变。有效地解决超调、跟踪速度、鲁棒性等问题，使系统更好地保持稳定性，提高系统的控制品质。

符号说明：

g——重力加速度，m·s－2；

Sj——液膜厚度，m；

V——y方向液体流速，m·s－1；

R1——蒸发器的半径，m；

Xi1——组分i在蒸发器膜表面的摩尔分率；

P0i——组分i的饱和蒸气压，Pa；

Xi2——组分i在冷凝器膜表面的摩尔分率；

T1w——冷凝器的壁面温度，K；

Rg——气体常数，J·mol－1·K－1；

Mi——组分i的摩尔分率，kg·kmol－1。

［1］ 陈增强，车海平．具有比例积分结构的广义预测自校正控制器［J］．控制与决策，1994，9（2）：106－108．

［2］ 王伟．广义预测控制理论及其应用［M］．北京：科学出版社，1998．

［3］ Li Guo－bing，Wiped－film．Molecular disthllation process［J］．Tianjin Univesity，2005（12）：35－37．

［4］ 冯武文，杨村，于宏奇．分子蒸馏技术及其应用［J］．化工进展，1998（6）：26－29．

［5］ 李国兵，许春建，周明．刮膜分子蒸馏传质和传热的数学模型［J］．天津大学学报，2003，36（3）：261－266．

［6］ 李桂娟，徐雪丽，宋伟．天然维生素E的提取［J］．长春工业大学学报：自然科学版，2006，27（3）：20－24．

［7］ 张旭斌．分子蒸馏过程研究［D］：［硕士学位论文］．天津：天津大学，2003

［8］ Clarke D W，Mohtadi C，Tuffs P S．Generaliced predutuve control－part［J］．The Basic Algorithm Automatica，2007，23：127－148．