非标准HFS－B问题的设备协同调度研究＊

张 煜 匡家喜 李文锋 容芷君

（武汉理工大学物流工程学院1） 武汉 430063） （武汉科技大学汽车与交通工程学院2） 武汉 430081）

0 引 言

传统集装箱装卸系统中的设备调度问题，可以描述为带阻塞的混合流水车间（hybrid flow shop problem with blocking，HFS－B）问题［1－2］：在任意时空，系统中仅存在一种箱流，箱流中的任意集装箱都经历相同的3个阶段；各个阶段都对应一个并行机集合；相邻阶段之间无缓冲区；集装箱在每个阶段的操作，都对应一个处理时间.这种标准的 HFS－B 问题，广泛存在于电子制造［3］、钢铁［4］、纺织［5］、港口［6］等流程工业中.

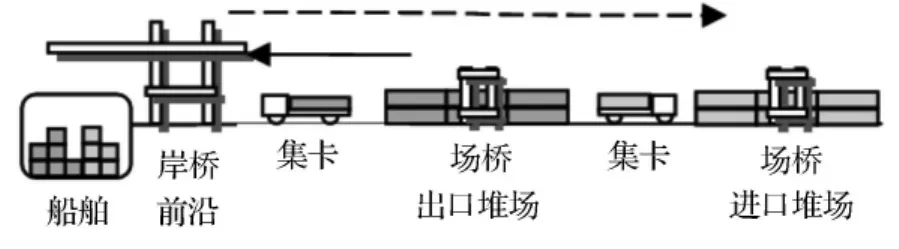
图1 采用边装边卸工艺的集装箱作业系统

目前，采用同贝位边装边卸（dual－cycle或double－cycling）工艺的港口集装箱装卸系统［7］，如图1所示，有别于传统的集装箱装卸系统，体现为2种流程互逆的箱流（进口和出口箱流）同时存在，这类系统内的设备调度问题可以被描述为非标准的 HFS－B问题或Bidirectional FSP（BiFSP）问题［8］，其主要特征为：系统中同时存在2种流向互逆的工件流；同流向的工件，都经历3个相同的阶段，相邻阶段无缓冲区；第2阶段设备的准备和处理时间不是预先可知的，与设备当前工件的紧前和紧后操作的机器位置相关.

非标准HFS－B环境内的港口设备调度问题研究，需要综合考虑设备之间的工作量均衡、箱流的平稳流畅，以上都离不开非标准HFS－B环境内不同阶段之间设备协同能力的研究，即非标准HFS－B问题的设备协同研究.由于标准的HFS－B问题属于NP－hard，精确算法难于求解大规模实际案例，因而启发式算法、元启发式算法被广泛用于实际生产环境中HFS－B问题的求解.本文的研究内容是构建快速高效的3阶段决策的启发式算法，求解这类非标准HFS－B环境下的实际大规模案例，以提高设备之间的协同能力.

1 启发式算法

1.1 堆场空间决策

该决策子问题可以描述为不平衡运输和分配问题.以进口箱为例，已知有m个岸桥，进口箱堆区有n个区块，第i个岸桥需要执行的进口箱任务为ai（i＝1，2，…，m），第j个区块能够接收的箱量为bj（j＝1，2，…，n），从第i个 QC到第j个区块的最短水平输送时间为tij，则如何确定任意区块j从任意岸桥i接收的进口箱量xij，使总水平输送时间最短.该类问题的数学模型为

目标函数（1）要求总的水平运输时间最短；约束（2）对应流平衡约束，保证任意岸桥需要执行的进口箱任务都能被分配给集卡，执行运输任务；约束（3）对应能力约束，保证任意区块或区段（block）接收的进口箱量不能溢出.该数学模型为线性方程，变量数为m×n个，当码头规模较大时（例如：4个泊位，24个QC，48个进口区块），变量数通常上千，很难在较短时间实现问题的精确求解.

1.2 任务分配决策

任务分配决策可以描述为：有n个集装箱作业任务（主要涉及前沿操作、水平输送、堆场操作等环节的作业任务）和m个设备（主要涉及岸桥、集卡、场桥）；任意设备i的最大加工能力，即设备i最多可处理的装卸任务数，记为bi，TEU；如果将任务j分配给设备i，记xij＝1，同时产生费用或成本cij；当装卸任务j对应的集装箱为20或40英尺箱，rij分别取值1或2TEU；决策的目标是如何分配任务给设备，使总成本最小（成本可以是时间、距离、费用等）.该类问题的数学模型可以表示为

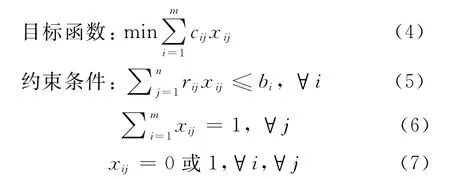
目标函数（4）要求总的成本最小；约束（5）保证任意设备加工的工件数不能超过其加工能力；约束（6）保证任意任务都能被唯一分配给某台设备；约束（7）保证xij为0－1变量.对于此类任务分配问题，Robert M.Nauss指出其为NP－hard问题［9］，很难在多次项时间内获得其最优解.

1.3 设备调度决策

通过分析设备的顺序约束和协同关系（见图2），利用仿真时间的变化和事件的触发，对设备的状态空间进行更新.基于以上状态的转移和当前时刻，确定设备处理当前任务的开始和结束时间，以及当前工件离开该设备的时间.

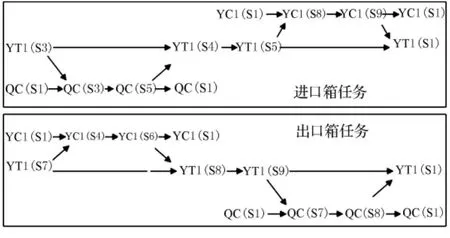
图2 设备的顺序约束和协同关系

图2 中，YT1，YC1，QC分别表示集卡、场桥、岸桥等设备；括号中的内容表示设备的状态；箭头表示顺序约束和协同关系；集卡的S1、S3，S4，S5，S7，S8，S9分别表示空闲、前沿空车排队、重车前往堆场、堆场重车排队、空车前往堆场、堆场空车排队、重车前往前沿、前沿重车排队等状态；场桥的S1，S4，S6，S8，S9分别表示空闲、提取集装箱、装车、卸车、堆码集装箱等状态；岸桥的S1，S3，S5，S7，S8分别表示空闲、卸船、装车、卸车、装船等状态.

1.4 3阶段启发式算法

结合以上决策子问题描述和策略，图3给出了3阶段决策的启发式算法.图中，集合D表示空闲和即将空闲的集卡集合，通过集卡的工作状态进行判别；Si＝S0表示当前工班的集卡是否全部都为非激活状态的集卡，用于判别算法是否结束；算法主要有堆场空间决策、任务分配决策和设备调度决策等内容组成，详细描述如下.

图3 三阶段决策的启发式算法

堆场空间决策采用基于Fill ratio的启发式算法，核心思想是：堆场各区块（block）的fill ratio大致均衡，这意味着可以均衡分配工作量，从而避免局部的交通堵塞，因此就可以将港口路网的不平衡运输和分配问题转化为Fill ratio的均衡问题，从而大大降低了变量数和运算的复杂度.此处，任意区块i的Fill ratio用fi表示，＝（ai＋xi）／A.式中：ai，xi，A分别为区块i的初始箱量、区块i的配额、区块的最大容量；xi为决策变量，其他为已知量.

任务分配决策采用基于库存和配额的表调度理论，核心思想是：将当前可得任务按FIFO策略排序和构建任务表单Ltask，将当前空闲设备按库存非减和配额非增进行排序和构建设备表单Le，实现两个表单元素的一一配对，当任意表单为空，算法结束.

2 仿真实验

假设：某集装箱码头分为进、出口堆场；前沿、陆域长度皆为1 000m；岸桥、场桥、集卡等设备的基本参数分别设置为48moves／h，20moves／h，30 km／h（空车）或20km／h（重车）；岸桥和场桥的处理时间服从正态分布，均值采用以上基本参数.

构建4个案例，见表1.每个案例仿真20次，置信区间为90%，主要实验结果见图4.以上案例的CPU时间都小于2s.

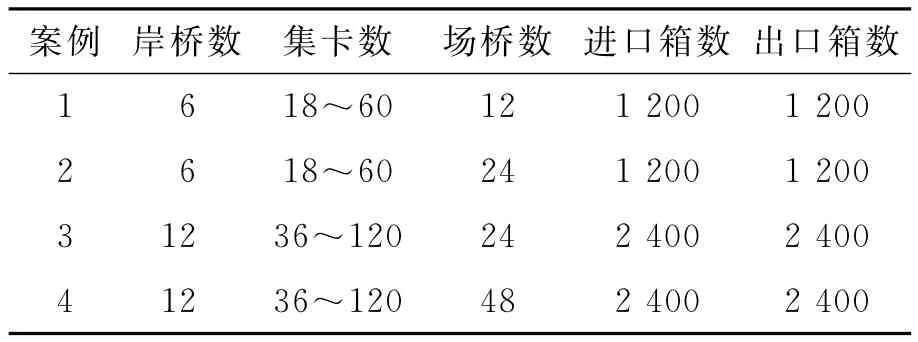
表1 案例

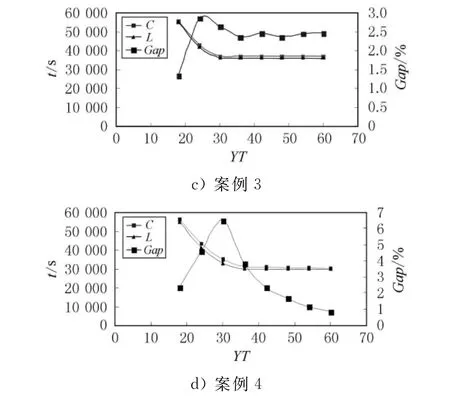
图4 仿真结果

图4 中，横坐标对应当前工班的集卡数量，左边的纵坐标对应makespan时间，右边纵坐标对应Gap；C，L，Gap分别为启发式算法获得的makespan时间、makespan时间的理论下界、（CL）／L；理论下界L采用了基于阶段的下界理论［10］和基于 makespan的下界理论［11］，取两者的最大值.

图4中，每个案例下的C和L曲线都对应一个折点（knee point－KP），说明：（1）在 KP左侧，提高集卡数量能够显著降低makespan时间；（2）在KP右侧，提高集卡数量不能显著降低makespan时间.以上揭示了合理的当前工班集卡数量在KP附近，也反映了当前工班的集卡数量与系统的makespan之间的关系.

基于以上结论，可知KP附近的最大Gap是小于4%.因而，根据Gap特性的分析，能够揭示：（1）本文开发的算法具有较好的特性；（2）通过合理选择当前工班的集卡数量，能够避开最差的情形.

3 结束语

从采用dual－cycle工艺的集装箱装卸系统中提炼了一种非标准的HFS－B问题，该问题具有以下特点：具有互逆的2种工件流，某些阶段机器的处理时间和准备时间不预先可知，无缓冲区等.该问题的NP－hard特性，促使我们开发了3阶段决策的启发式算法，对这类实际背景下的HFS－B问题进行求解.大量实验仿真数据表明：（1）开发的算法能够在2s内求解本文所提供的大规模场景案例；（2）算法的最大Gap不大于7%；（3）仿真结果表明合理的工班集卡数量处于knee point附近；（4）当取knee point附近的集卡数量作为当前工班的集卡数，最大Gap不大于4%.综上，本文所开发的3阶段启发式算法具有快速高效的性能，特别适合百万吨海港设备的协同调度.

［1］Ruiz R，JoséAntonio Vázquez－Rodríguez.The hybrid flow shop scheduling problem［J］.European Journal of Operational Research，2010，205 （1）：1－18.

［2］Chen L，Bostel N，Dejax P，et al.A tabu search algorithm for the integrated scheduling problem of container handling systems in a maritime terminal［J］.European Journal of Operational Research，2007，181（1）：40－58.

［3］Choi Hyunseon，Kim Hyungwon，Lee Dongho，et al.Scheduling algorithms for two－stage reentrant hybrid flow shops：minimizing makespan under the maximum allowable due dates［J］.The International Journal of Advanced Manufacturing Technology，2009，42（9－10）：963－973.

［4］Atighehchian A，Bijari M，Tarkesh H.A novel hybrid algorithm for scheduling steel－making continuous casting production［J］.Computers ＆ Operations Research，2009，36（8）：2 450－2 461.

［5］Montoya－Torres J R，Vargas N F.Solving a bi－crite－ria hybrid flowshop scheduling problem occurring in apparel manufacturing［J］.International Journal of Information Systems and Supply Chain Management，2011，4（2）：42－60.

［6］Zeng Qingcheng，Yang Zhongzhen.Integrating simulation and optimization to schedule loading operations in container terminals［J］.Computers ＆Operations Research，2009，36（6）：1 935－1 944.

［7］Goodchild A V，Daganzo C F.Double－cycling strategies for container ships and their effect on ship loading and unloading operations［J］.Transportation Science，2006，40（4），473－483.

［8］ZhengYi，John Zhao，Hoong Chuinlau，et al.Integrated resource allocation and scheduling in a bidirectional flowshop with multimachine and COS constraints［J］.IEEE Transactions on Systems，Man，and Cybernetics－Part C，2009，39（2）：190－200.

［9］Nauss R M.Solving the generalized assignment problem：an optimizing and heuristic approach［J］.INFORMS Journal on Computing，2003，15（3）：249－266.

［10］Santos D L，Hunsucker J L，Deal D E.Global lower bounds for flow shops with multiple processors［J］.European Journal of Operational Research，1995，80（1）：112－120.

［11］Bish E K.A multiple－crane－constrained scheduling problem in a container terminal［J］.European Journal of Operational Research，2003，144（1）：83－107.